回归算法最小角回归（LARS）通过高维数据的线性组合提供变量。
它与正向逐步回归有关。在这种方法中，在每个步骤中选择最相关的变量，其方向在两个预测因子之间是等角的。
在本教程中，我们将学习如何用Python中的LARS和Lasso Lars算法拟合回归数据。LARS算法是一种用于回归分析的算法，它可以处理高维数据，并且能够自动选择最重要的特征。Lasso Lars算法是LARS算法的变种，它引入了L1正则项，以减少模型的复杂度和防止过拟合。在本教程中，我们将使用Python中的statsmodels库来实现LARS和Lasso Lars算法。我们将首先加载住房数据集，然后使用LARS和Lasso Lars算法对数据进行拟合。最后，我们将比较这两个算法的结果，并讨论它们的优缺点。我们将在本教程中估计住房数据集。这篇文章包括
可下载资源
作者
- 准备数据
- 如何使用LARS
- 如何使用Lasso LARS
让我们从加载所需的包开始。
from sklearn import linear_model准备数据
我们将加载波士顿的数据集，并将其分成训练和测试两部分。
boston = load_boston()
xtrain, xtest, ytrain, ytest=train\_test\_split(x, y, test_size=0.15)如何使用LARS
我们将用Lars()类定义模型（有默认参数），并用训练数据来拟合它。
Lars().fit(xtrain, ytrain)并检查模型的系数。
print(lars.coef_)
\[-1.16800795e-01 1.02016954e-02 -2.99472206e-01 4.21380667e+00
-2.18450214e+01 4.01430635e+00 -9.90351759e-03 -1.60916999e+00
-2.32195752e-01 2.80140313e-02 -1.08077980e+00 1.07377184e-02
-5.02331702e-01\]
接下来，我们将预测测试数据并检查MSE和RMSE指标。
mean\_squared\_error(ytest, ypred)
print("MSE: %.2f" % mse)
MSE: 36.96
print("RMSE: %.2f" % sqrt(mse))
RMSE: 6.08最后，我们将创建绘图，使原始数据和预测数据可视化。
plt.show()如何使用Lasso Lars
LassoLars是LARS算法与Lasso模型的一个实现。我们将用LassoLars()类定义模型，将α参数设置为0.1，并在训练数据上拟合模型。
LassoLars(alpha =.1).fit(xtrain, ytrain)我们可以检查系数。
print(coef_)
\[ 0. 0. 0. 0. 0. 3.00873485
0. 0. 0. 0. -0.28423008 0.
-0.42849354\]接下来，我们将预测测试数据并检查MSE和RMSE指标。
predict(xtest)
print("MSE: %.2f" % mse)
MSE: 45.59
print("RMSE: %.2f" % sqrt(mse))
RMSE: 6.75最后，我们将创建绘图，使原始数据和预测数据可视化。
plt.show()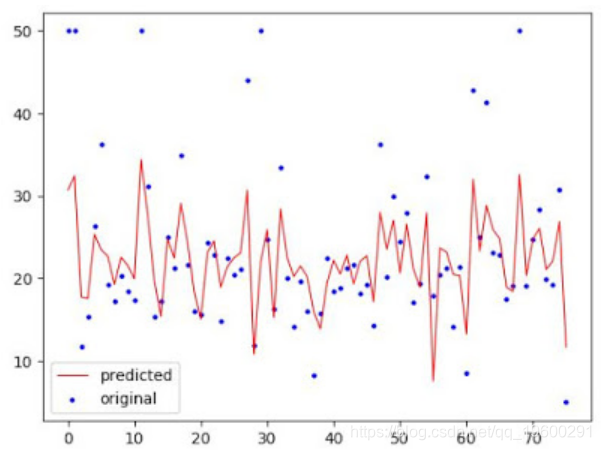
随时关注您喜欢的主题
在本教程中，我们已经简单了解了如何用LARS和Lasso Lars算法来拟合和预测回归数据。
参考文献
- Least Angle Regression, by Efron Bradley; Hastie Trevor; Johnstone Iain; Tibshirani Robert (2004)
- Least-Angel Regression, Wikipedia
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据：旅游市场差异、价格预测
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
