假设我们期望因变量由潜在协变量子集的线性组合确定。
然后,LARS算法提供了一种方法,可用于估计要包含的变量及其系数。
LARS解决方案没有给出矢量结果,而是由一条曲线组成,该曲线表示针对参数矢量L1范数的每个值的解决方案。
可下载资源
该算法类似于逐步回归,但不是在每个步骤中都包含变量,而是在与每个变量的相关性与残差相关的方向上增加了估计的参数。
范数(norm)
向量的范数
向量的 1-范数: 向量内各元素的绝对值之和
向量的 2-范数: 元素的平方和再开平方,一般就直接写
不加下标了。
向量的 p-范数:
向量的无穷范数:
矩阵的范数
矩阵的 1-范数: 矩阵的每一列上的元素绝对值先求和,再从中取个最大的(列和最大)
矩阵的 2-范数: 其中
为
的特征值,2-范数即为矩阵
的最大特征值开平方。
矩阵的无穷范数: 矩阵的每一行上的元素绝对值先求和,再从中取最大的(行和最大)。但还有一种情况,在很多的统计论文中,更常用的是把矩阵的无穷范数定义为矩阵中最大的元素:
这里只是借机会都给大家列出来了,本文并不需要用到这么多种范数。
Lasso原理
与岭回归类似,Lasso就是在目标函数 后面加了一个1-范数
Lasso的提出在岭回归之后,为啥加1-范数的Lasso没有加2-范数的岭回归早?
可能是因为1-范数作为绝对值之和不方便求导吧(个人猜测),因为做理论统计的学者提出一个新方法,不光要说明这个方法好,还要说明为啥好、哪里好。
为什么至今Lasso仍长青不老?
因为它可以解决现在高维数据一个普遍问题——稀疏性。高维数据即 的情况(超高维是
,这里不讨论),现在随着数据采集能力的提高,变量(也叫特征)数采集的多,但是其中可能有很多特征是不重要的,系数很小,如果用岭回归,可能这个不重要的变量也给你估出来了,而且可能还不小,而用Lasso方法,就可以把这些不重要变量的系数压缩为0,既实现了较为准确的参数估计,也实现了变量选择(降维)。
优点:
1.计算速度与逐步回归一样快。
2.它会生成完整的分段线性求解路径,这在交叉验证或类似的模型调整尝试中很有用。
3.如果两个变量与因变量几乎同等相关,则它们的系数应以大致相同的速率增加。该算法因此更加稳定。
4.可以轻松对其进行修改为其他估算模型(例如LASSO)提供解决方案。
5.在p >> n的情况下有效 (即,当维数明显大于样本数时)。
缺点:
1.因变量中有任何数量的噪声,并且自变量具有 多重共线性 ,无法确定选定的变量很有可能成为实际的潜在因果变量。这个问题不是LARS独有的,因为它是变量选择方法的普遍问题。但是,由于LARS基于残差的迭代拟合,因此它似乎对噪声的影响特别敏感。
2.由于现实世界中几乎所有高维数据都会偶然地在某些变量上表现出一定程度的共线性,因此LARS具有相关变量的问题可能会限制其在高维数据中的应用。
Python代码:
import matplotlib.pyplot as plt # 绘图
diabetes
查看数据
x /= np.sqrt(np.sum((x)**2, axis=0)) # 归一化 x
lars.steps() # 执行的步骤数
est = lars.est() # 返回所有LARS估算值
plt.show()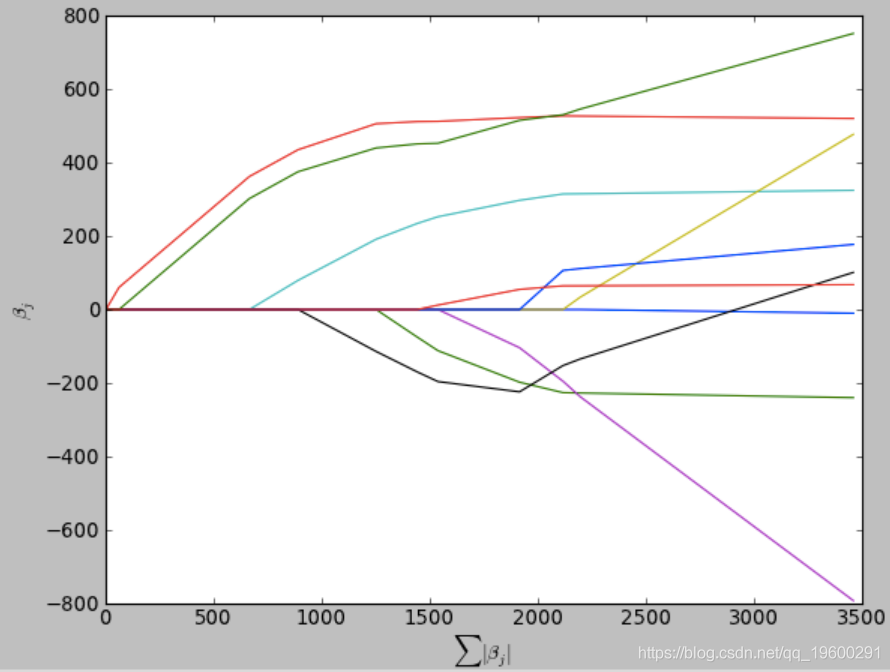


 Python用SentenceTransformer、OLS、集成学习、模型蒸馏情感分类金融新闻文本|附代码数据
Python用SentenceTransformer、OLS、集成学习、模型蒸馏情感分类金融新闻文本|附代码数据 Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据
Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据 Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据
Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据 Python、R语言分析在线书籍销售数据:梯度提升树GBT、岭回归、Lasso回归、支持向量机SVM实现多维度特征的出版行业精准决策优化与销量预测|附代码数据
Python、R语言分析在线书籍销售数据:梯度提升树GBT、岭回归、Lasso回归、支持向量机SVM实现多维度特征的出版行业精准决策优化与销量预测|附代码数据



