这篇文章介绍了一类离散随机波动率模型。
介绍了一些特殊情况,包括 GARCH 和 ARCH 模型。
可下载资源
本文展示了如何模拟这些过程以及参数估计。本文为这些实验编写的 Python 代码在文章末尾引用。
1.价格换对数收益,价格部分最好是GBM
2.garch有自回归,这种假设不太适合出现在收益(和价格上),一般出现在波动率上(如果你假设他有波动率。所以你其实需要的SV模型波动率部分选garch型
3.SV的布朗项指数为一般能选1/2(heston型),1(garch型)和3/2(3/2型)。这三种过程对应波动率对随机因子的缩放程度,可以理解为三种假设(或者观点),选什么看自己风险偏好。 (不过流通比较广的“3/2模型”的均值部分并不是heston型。)
4.如果没有对应产品,这种建模其实是一种对样本内的参数校准(即,对历史样本拟合随机过程的参数)。这个行为本身不是特别建议,特别是对于SV模型的样本内校准,难度很大,准度很差,而且还必须假设某种时间齐次
离散随机波动率模型
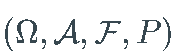 是一个随机基,有一个完整的
是一个随机基,有一个完整的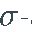
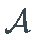 的可测量子集
的可测量子集  , 一个概率测量
, 一个概率测量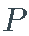 和一个过滤
和一个过滤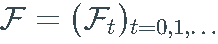
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
- 因此,时间实例使用非负整数进行索引
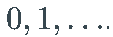
- 获取序列的第一个 t元素
 , 记号
, 记号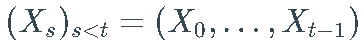 .
.
_离散随机波动率_( DSV) 模型 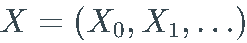 是一个实值 stochastic process (一系列随机变量)满足以下方程:
是一个实值 stochastic process (一系列随机变量)满足以下方程:
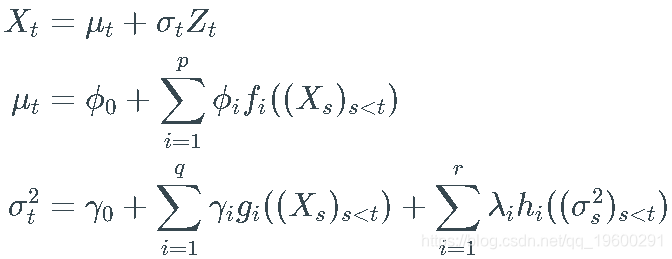
其中:
- Z 是 F 的噪声过程。
- φi 是实数,我假设
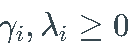 并且 gi ,hi 是非负值。
并且 gi ,hi 是非负值。 - fi 、gi 和 h_ihi 是过程的确定性函数。
- 过程
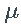 通常称为 _偏移_,而 σ 称为 X的_波动率。_因为σ 是一个随机过程,所以上面定义的过程 X 属于一个随机波动率模型的大家族。
通常称为 _偏移_,而 σ 称为 X的_波动率。_因为σ 是一个随机过程,所以上面定义的过程 X 属于一个随机波动率模型的大家族。 - 对于噪声过程 Z,使得每个 Z_t的均值和方差都存在,我们有
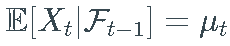 和
和 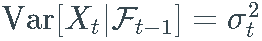 .
.
案例
制定通用 DSV 模型的特化:
后移算子 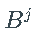 ,对于
,对于  ,产生其参数过程的滞后版本,即
,产生其参数过程的滞后版本,即 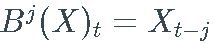 , 和
, 和 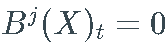 , 如果
, 如果 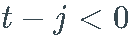 . 例如
. 例如
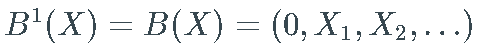
为方便起见,我设置 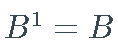 和
和 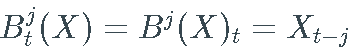 .
.
对于下面列表中的所有特殊情况,我假设函数 f\_i、gi 和 hi 从参数过程的历史中选择一个元素,即 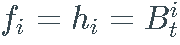 , 和
, 和 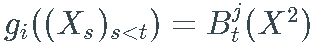 .
.
GARCH 过程定义另外设置 。
。
_GARCH(1, 1)_过程非常流行:
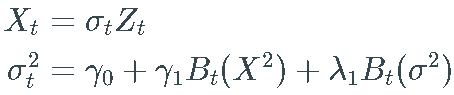
在 ARCH 过程中,波动性具有简化形式,对于所有 i,λi = 0,并且  。
。

_ARCH(1)_过程还 满足 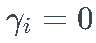 对所有
对所有  :
:
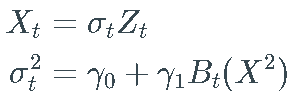
模拟
离散随机波动率模型通常用于对观察到的时间序列的对数收益进行建模。因此,为了模拟原始时间序列的路径,我们需要模拟其对数收益并计算 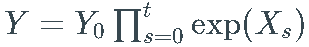 .
.
由带参数的高斯噪声驱动的 GARCH(1,1) 过程的样本路径  :
:
path( \[0.001, 0.2, 0.25\]) cumprod* repeat.reshape plt.subplots
随时关注您喜欢的主题
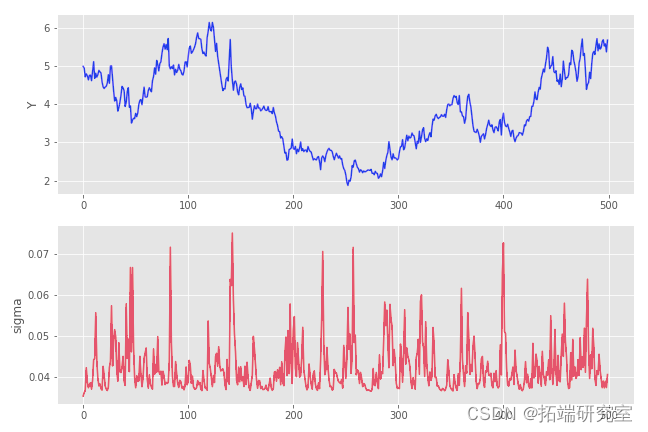
注意 σ 过程为  不能低于
不能低于 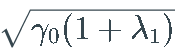 ≈0.0353
≈0.0353
最大似然估计
最大似然(ML)参数估计是所有讨论模型的选择方法,因为转换密度,即给定过去信息的 X_t 的密度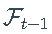 是明确已知的。因此,过程样本路径 x 的对数似然函数由下式给出
是明确已知的。因此,过程样本路径 x 的对数似然函数由下式给出
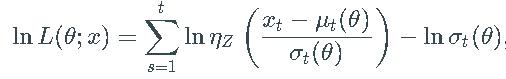
其中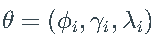 ,而
,而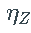 是 Z的密度。将上述对数似然函数最小化可得到
是 Z的密度。将上述对数似然函数最小化可得到 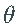 的最大似然估计
的最大似然估计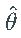 :
:
 .
.
蒙特卡罗研究
为了测试 ML 参数估计过程,我进行了以下蒙特卡罗实验。
- 使用参数 (0.001, 0.2, 0.25) 模拟长度为 5000 的 2500 个独立 GARCH(1,1) 过程路径。我使用了高斯噪声,即
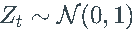 .
. - 将这些路径中的每一个都输入到 ML 估计并获得估计的参数向量
 .
. - 此优化过程中参数的搜索范围限制为 [1e-8, 1]。
- 将原始
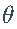 与估计的
与估计的 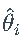 进行比较。
进行比较。 - 使用参数向量
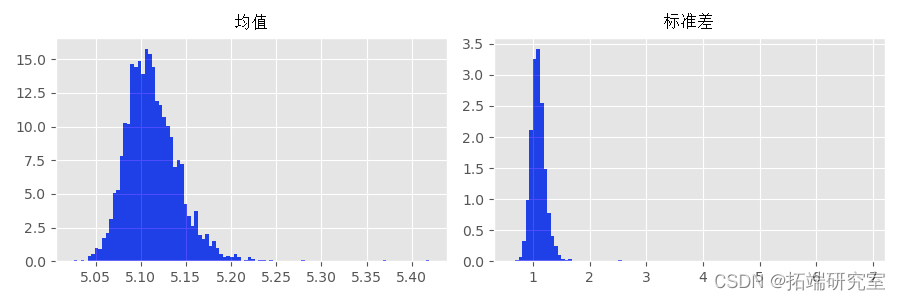
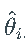 模拟 GARCH(1,1),计算均值和标准差,并将它们与“真实”均值和标准差(分别为 5.098 和 1.084)进行比较。
模拟 GARCH(1,1),计算均值和标准差,并将它们与“真实”均值和标准差(分别为 5.098 和 1.084)进行比较。
正如期望的那样,估计量 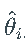 非常不准确,并且在大多数情况下,甚至不接近真实向量
非常不准确,并且在大多数情况下,甚至不接近真实向量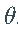 。特别是,估计的
。特别是,估计的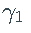 和
和 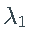 通常设置为零(参见下面的直方图)。
通常设置为零(参见下面的直方图)。
ps = \[0.001, 0.2, 0.25\] cumprod * repeat print, np.std

另一方面,来自估计的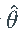 的过程均值和标准偏差要准确得多。这是一件好事,因为我们通常更关心恢复未知数据生成过程的特征,而不是模型的真实参数值。
的过程均值和标准偏差要准确得多。这是一件好事,因为我们通常更关心恢复未知数据生成过程的特征,而不是模型的真实参数值。
mes, stvs, esms ax\[1\].hist fig.tight_layout
噪声过程 不必归一化为均值 0 和方差 1。
柯西噪音
实际上,我们只需要确保随机变量 Zt 的分布具有密度即可。如果是这种情况,过程模拟和 ML 估计都可以按照描述的方式工作。
那么如何用从柯西分布中采样的噪声替换高斯噪声呢?在许多概率论书籍中,柯西分布被用作反例,因为它具有许多“病态”特性。例如,它没有均值,因此也没有方差。
我不知道柯西分布中的不稳定样本是什么样子的。看一下带有参数向量的 GARCH(1,1) 过程的示例路径 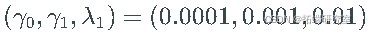 :
:
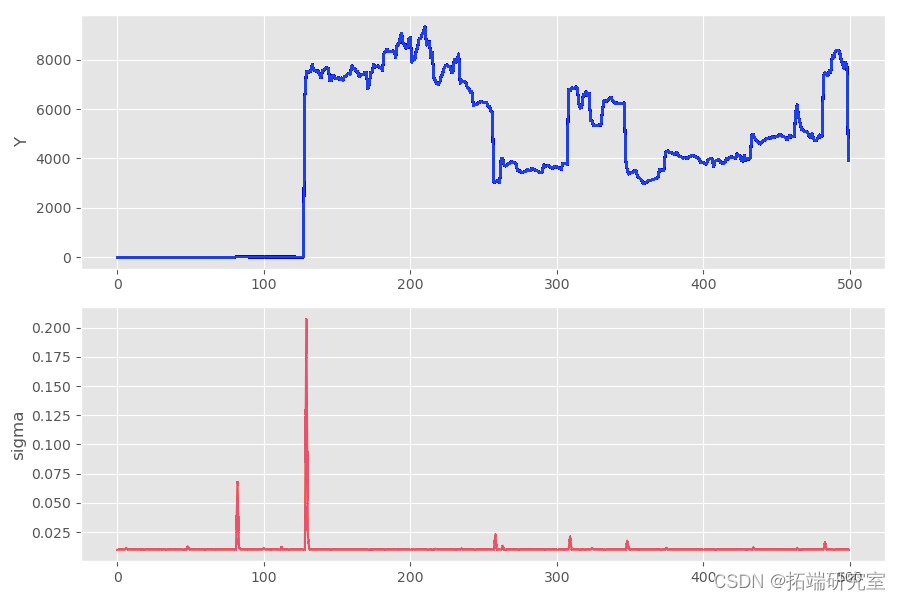
如果使用路径生成函数的时间足够长,甚至可能会生成溢出异常。因此,我用来生成上面显示的直方图的 Python 函数失败了。为了了解原因,让我们使用来自柯西分布的样本生成一些直方图:
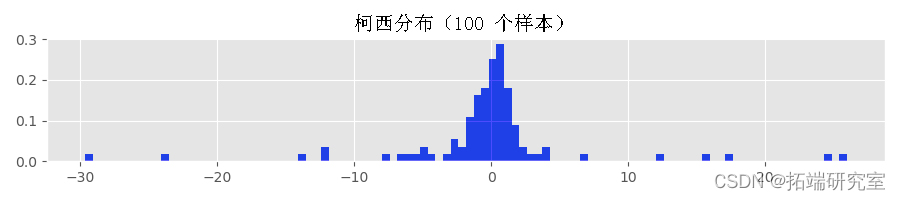
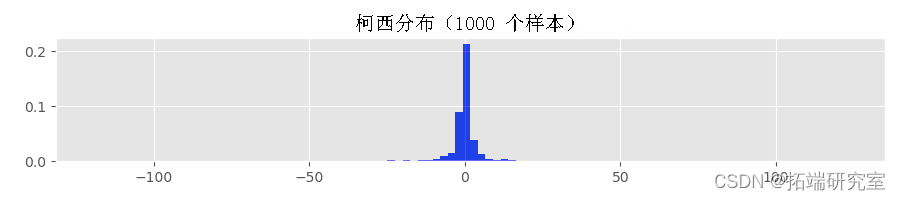

柯西分布具有分位数函数
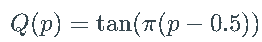
对  评估
评估 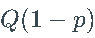 给出
给出
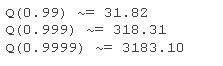
这意味着,例如,在 0.0001 的概率下,采样值大于 3183.10。为了比较,让我们计算标准正态分布的相应分位数:
norm.ppf(0.99)
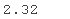
norm.ppf(0.999)
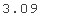
norm.ppf(0.9999)
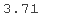
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据 Python比特币价格时间序列:LGBMRegressor递归自回归、随机游走及外部变量预测探索
Python比特币价格时间序列:LGBMRegressor递归自回归、随机游走及外部变量预测探索
