最近我们被客户要求撰写关于波动率的研究报告,波动率是一个重要的概念,在金融和交易中有许多应用。它是期权定价的基础。波动率还可以让您确定资产配置并计算投资组合的风险价值 (VaR)。
甚至波动率本身也是一种金融工具,例如 CBOE 的 VIX 波动率指数。然而,与证券价格或利率不同,波动性无法直接观察到。
相反,它通常被衡量为证券或市场指数的收益率历史的统计波动。这种类型的度量称为已实现波动率或历史波动率。
衡量波动性的另一种方法是通过期权市场,其中期权价格可用于通过某些期权定价模型得出标的证券的波动性。Black-Scholes 模型是最受欢迎的模型。这种类型的定义称为 _隐含波动率_。VIX 基于隐含波动率。
存在多种统计方法来衡量收益序列的历史波动率。高频数据可用于计算低频收益的波动性。例如,使用日内收益来计算每日波动率;使用每日收益来计算每周波动率。还可以使用每日 OHLC(开盘价、最高价、最低价和收盘价)来计算每日波动率。
比较学术的方法有ARCH(自回归条件异方差)、GARCH(广义ARCH)、TGARCH(阈值GARCH)、EGARCH(指数GARCH)等。我们不会详细讨论每个模型及其优缺点。相反,我们将关注随机波动率 (SV) 模型,并将其结果与其他模型进行比较。一般来说,SV 模型很难用回归方法来估计,正如我们将在本文中看到的那样。
欧元/美元汇率
我们将以 2003-2018 年 EUR/USD 汇率的每日询价为例来计算每日波动率。
subplot(2,1,1); plot(ta,csl) subplot(2,1,2); plot(at,rtdan);
可下载资源
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
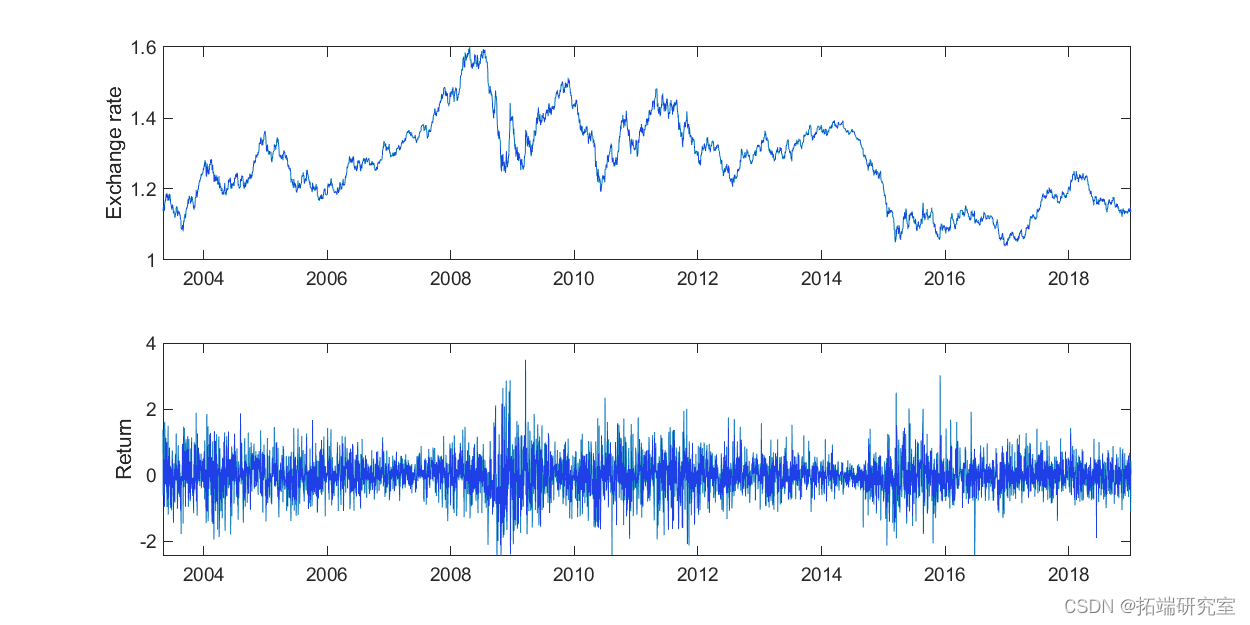
图 1. 顶部:欧元/美元的每日汇率(要价)。底部:每日对数收益率百分比。
图 2 显示收益率中没有序列相关性的依据。
\[sdd,slodgdL,infaso\] = estimaadte(Mddsdl,rtasd); \[aEass,Vad,lsagLd\] = infer(EstMsssddl,rtsdn); \[hsd,pValasdue,dstat,ascValue\] = lbqtest(reas,'lags',12) \[hs,pdValsue,sdtatsd,cVsalue\] = lbqtest(resss.^2,'lags',12)
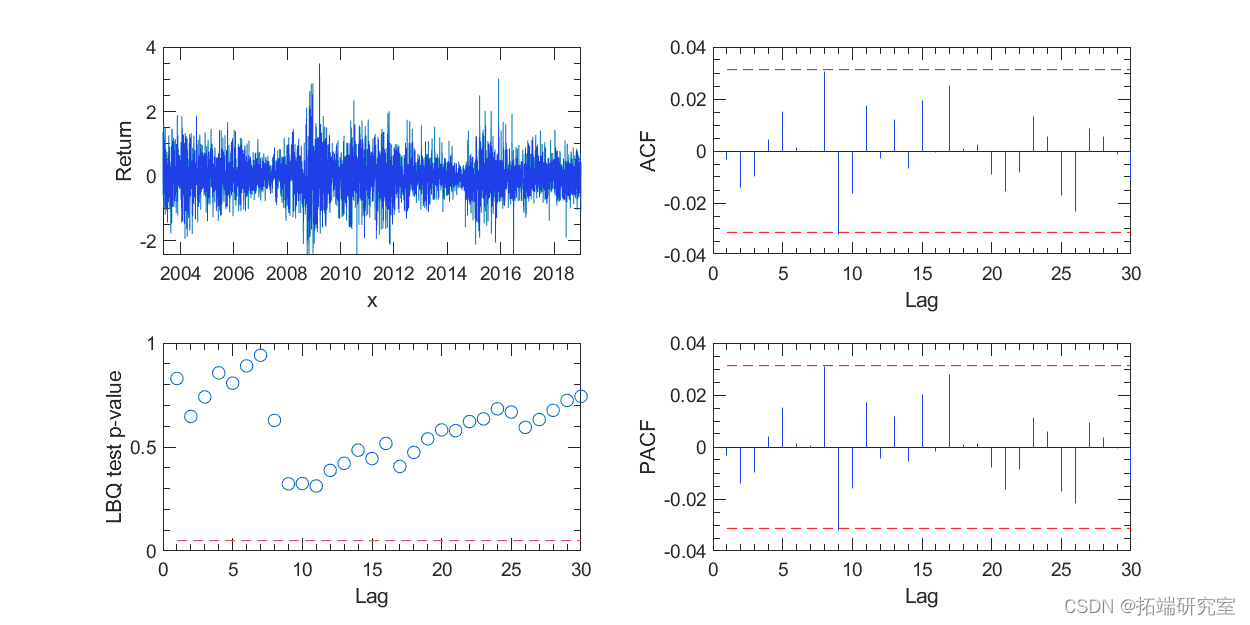
图 2. 收益率相关性检验。
Ljung-Box Q 检验(左下)没有显示显着的序列自相关作为收益率。
然而,我们可以很容易地识别出绝对收益率值较大的时期集群(无论收益率的符号如何)。因此,绝对收益值存在明显的序列相关性。
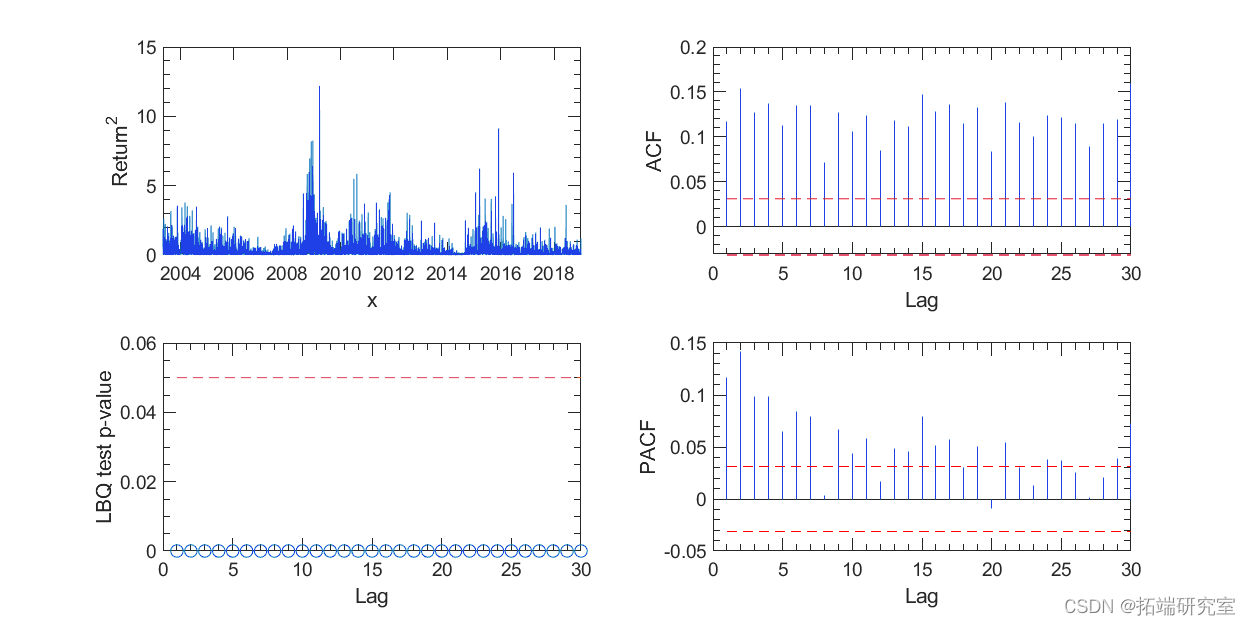
图 3. 回归平方的相关性检验。
GARCH(广义自回归条件异方差)模型
GARCH(1,1) 模型可以用 Matlab 的计量经济学工具箱进行估计。图 4 和图 5 中的 ACF、PACF 和 Ljung-Box Q 检验未显示残差及其平方值的显着序列相关性。图 4 左上图中的残差项在视觉上更像白噪声,而不是原始收益序列。
随时关注您喜欢的主题
Mdls.dsVadjnce = garc(1,1); \[EsastMdl,EssddkjParamsCovf,lsdoggL,isdjngfo\] = estimate(Msddl,rstan); \[Egf,hgV,logfgL\] = inffgher(EstsdMdl,arstn); gfh= Egh./sqrt(Vf);
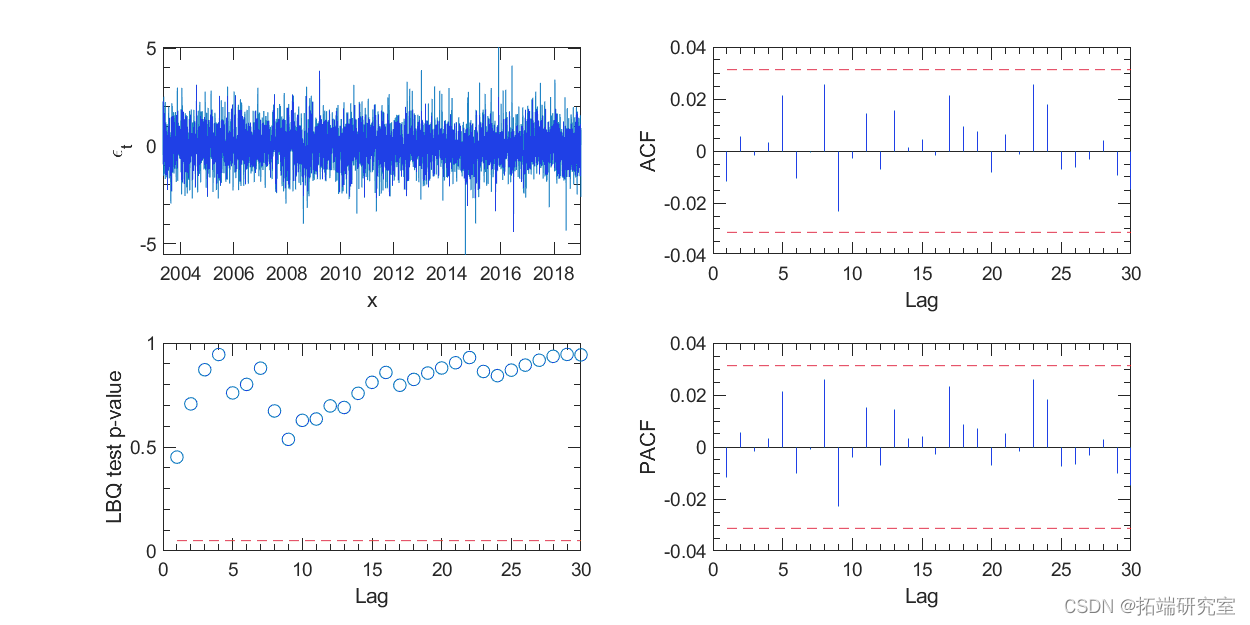
图 4. GARCH(1,1) 模型残差的相关性检验。
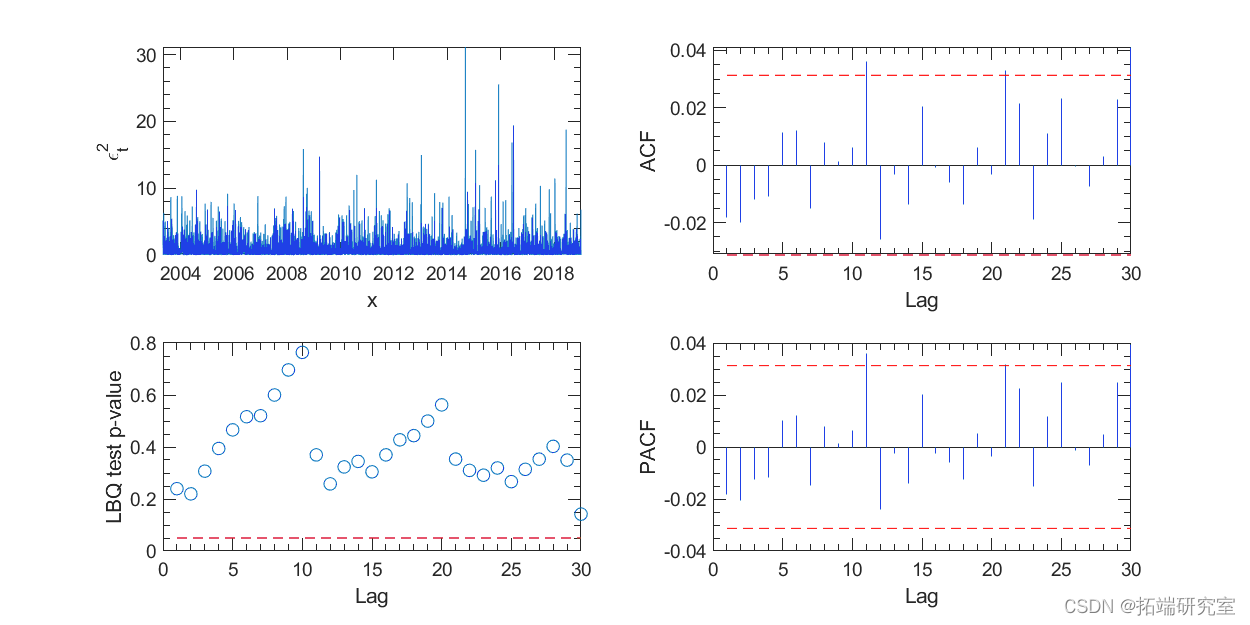
图 5. GARCH(1,1) 模型残差平方的相关性检验。
plot(at,dad)
set(gsdcaa);
set(gasdca);
ylabel('GARCH Volatility h_t');
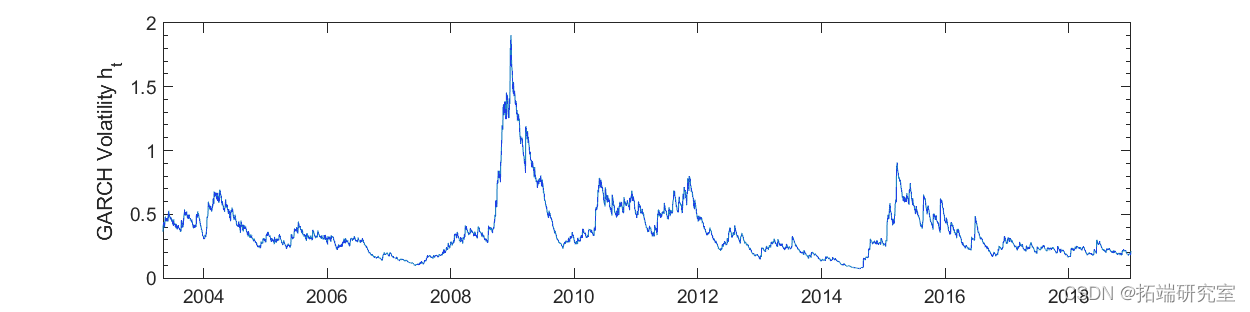
图 6. GARCH(1,1) 模型的波动率。
马尔可夫链蒙特卡罗 (MCMC)
MCMC 由两部分组成。_ 蒙特卡洛_ 部分处理如何从给定的概率分布中抽取随机样本。
马尔可夫 链 部分旨在生成一个稳定的随机过程,称为马尔可夫过程,以便通过蒙特卡罗方法顺序抽取的样本接近从“真实”概率分布中抽取的样本。
然后我们可以迭代地使用 Gibbs 采样 _方法来产生一系列参数。经常被丢弃,因为它除了使分布正常化之外什么都不做。后验分布是不完整的。_Metropolis 采样 方法和更通用的方法 Metropolis _-Hastings 采样_用于此场景。这两种采样方法更常用于难以制定完整条件后验分布的非共轭先验分布。
% --- MCMC
nmascmfgac = 10000;
bechvzta_mcmc = nan(nmc;dmc,1);
loxvgh_mcmc = nan(an,nmcjkldsmc);
alpha_mcmc = nan(nmcmssdc,length(alspdha0));
Sigmacvv_mcmc = nan(nmytsdcmc,1);
% --- 吉布斯抽样:beta
rtnas_new = rtn./sqdssrt(exp(logshis)); % 重新格式化收益系列
x = 1./sqrt(exp(lsogshisd));
V\_gfbeta = 1/(x'*x + 1/Sigsgfma\_bdeta0);g
E\_bgexta = V\_bfgetfga*(beta0/Sifgma\_beta0+gdfxf'*rtndf\_new);
betxa = cnormrnd(E\_beta,sqrt(fgV\_bfdfgeta));
% --- Metropolis 抽样:ht
loghn1 = alphjklai(1)+alphai(2)*(alphai(1)+alphai(2)*loghi(n-1));
loghf1 = \[loghi(2:end); loghn1\];前进一步 ht 的 % log
loghb1 = \[logh0;罗吉(1:end-1)\];后退一步 ht 的 % log
% - 提出新的 ht
lojkghp = normrnd(lohghjkli,sijlgma_jlogjhp);
% - 检查后验概率的对数比率
logr = log(normpdf(loghp, \[ones(n,1),loghb1\]*alphai',sqrt(Sigmavi))) + ...
% --- 吉布斯抽样 alpha
zasdt = \[ones(n-1,1),lokkghi(1:end-1)\];
V\_alpghas = inv( inv(Sigjkmahjg\_alpjha0) + zt'*zt/Si;gmavkl;i);
E\_aldfhpha = V\_alpha*(inv(Sigmjhja_abvnl;'lpha0)\*akllpha0' + zt'\*loghi(2:end)/Smavi);
alvbphai =v mvnrnd(E\_vbal,npnha,V\_bnm,bvalpha);
% --- 吉布斯抽样:Sigfmav
SfSR = sum((logfgjhi(2:ehgjnd)-zt*alphaighj').^2);
% 通过 OLS 获取 SSR 的替代方法
Sigjhavi = 1/randolhkm('Gamma',(nu0+n-1)/2,2/(nu0*Sigmavl;'k0+SSR));
随机波动率 (SV) 模型
对波动率进行随机建模始于 1980 年代初,并在 Jacquier、Polson 和 Rossi 的论文在 1994 年首次提供了随机波动率的明确证据后开始适用。波动率创新是 SV 和 GARCH 模型之间的主要区别。在 GARCH 模型中,时变波动率遵循确定性过程(波动率方程中没有随机项),而在 SV 模型中它是随机的。
然而,要获得概率分布的近似形式的归一化因子并不简单。
%% MCMC 用于随机波动率
% --- 先验参数
Sigwertma_aelpha0 = etdiagweetwr(\[0.4,0.4\]); % 协方差
% - 对于 sigrmea^2_v
nu0 = 1;
Sigemav0 = 0.01;
% --- 使用 GARCH(1,1) 模型的初始值,以及 log(ht0) 的最小二乘拟合
bewtwai = EstMtydl.rtyConrtystatynt;
MrgeyDL = etyrffitytlm();
alpefdgrtyhai = Mdl.Cvxoertyefficients{:,1}';
Sigretyrxmavi = nanvar(Mderyl.Reyefsidrdtyeruals.Raw);
我们可以使用暴力计算来为每个可能的值生成一个概率网格,然后从网格中绘制。这称为 Griddy Gibbs 方法。或者,我们可以使用 Metropolis 算法。在该算法中,要从中提取的提议分布可以是任何对称分布函数。提议分布函数也可以是不对称的。但在这种情况下,在计算从 跳到 的概率比率时,需要包含附加项以平衡这种不对称性。这称为 Metropolis-Hastings 算法。
可以使用 Metropolis-Hastings 算法的更复杂的提议方法来减少序列中的相关性,例如 Hamiltonian MCMC。
subplot(4,1,1); plot(beasdta_mcmc);
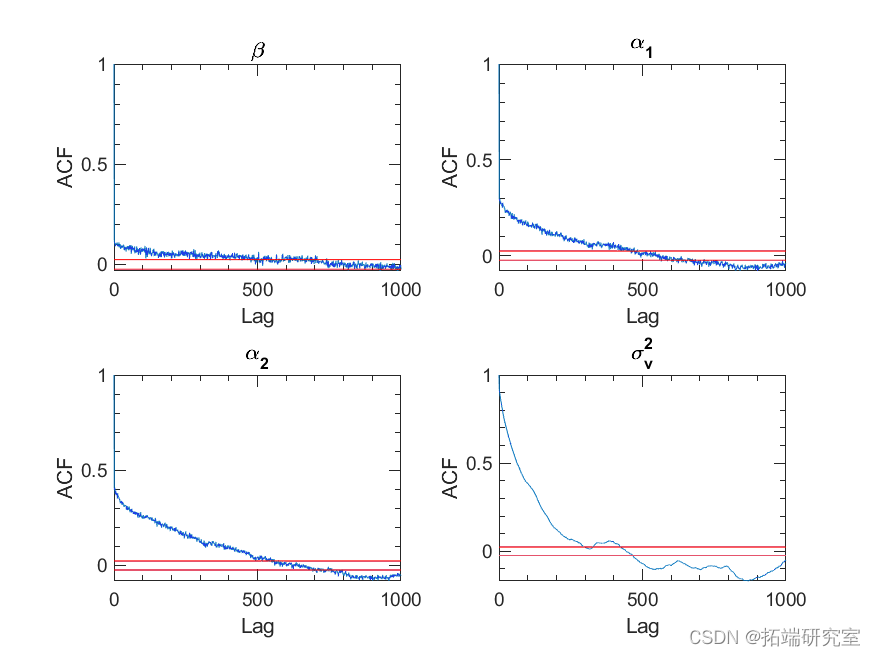
图 8. 预烧burin-in后参数序列的自相关。红线表示 5% 的显着性水平。
结果与讨论
去除burin-in后,我们从参数的真实高维联合分布中得到可以近似随机抽取的样本的参数样本集合。然后我们可以对这些参数进行统计推断。例如,成对参数的联合分布和每个参数的边际分布如图 9 所示。我们可以用联合分布来测试这个说法。显然与其余参数不相关。正如预期的那样,并且高度相关,使用它们的联合后验分布来证明采样的合理性。为了提高采样效率,降低序列中样本的相关性,我们可以通过采样改进上述算法,并从它们的三元联合后验分布。然而,如果不是完全不可能的话,为不同先验分布的变量计算出一个紧密形式的后验分布是很麻烦的。在这种情况下,Metropolis-Hastings 抽样方法肯定会发现它的优势。
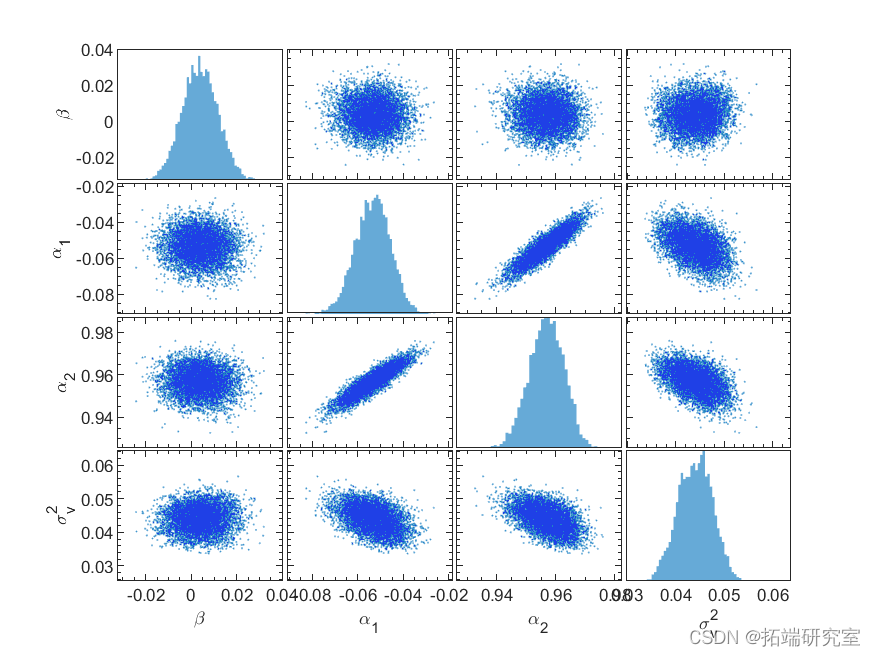
图 9. 成对参数联合分布的散点图(非对角面板)和参数边缘分布的直方图(对角面板)。
随机波动率及其置信带是通过计算序列稳定后采样波动率的均值和 2.5% 和 97.5% 分位数得到的。它绘制在图 10 中。
h\_mcmc = exp(logf\_mdsmc); nbudrin = 4000; lb = quanile(h_mcd,bunn+1:end),0.025,2); % 2.5% 分位数 ub = quatgjeh_mcmc(nburhjkin+1:end)fhjk,0.975,2); % 97.5% 分位数 holdghfd on; box on; plot(1:lengtgdhfh(t),V,'',dhfg1) plot(1:length(t),mdfghean(h_mcmc(:,nburnhgdf:enddgfh2),'linekljwdth',1)s
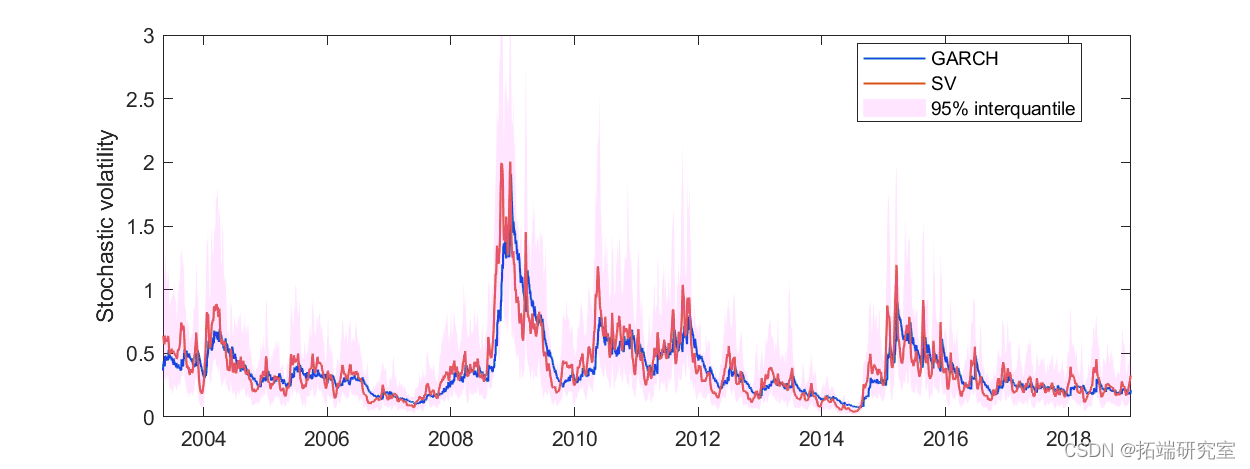
图 10. 4000 次burin-in迭代后随机波动率的后验平均值。对于置信带,随机波动率的 95% 分位数间以红色显示。
SV 模型的随机波动性总体上与 GARCH 模型非常相似,但更加参差不齐。这是很自然的,因为 SV 模型中假设了额外的随机项。与其他模型相比,使用随机波动率模型的主要优点是波动率被建模为随机过程而不是确定性过程。这使我们能够获得序列中每个时间的波动率的近似分布。当应用于波动率预测时,随机模型可以为预测提供置信度。另一方面,不利因素也很明显。计算成本相对较高。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程
llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别
Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
