---

可下载资源

P 和 Q 分别是 GARCH 和 ARCH 多项式中的最大非零滞后。其他模型参数包括平均模型偏移、条件方差模型常数和分布。

所有系数都是未知（NaN 值）和可估计的。

创建 GARCH(0,0) 模型。

garch

创建 GARCH 模型

garch 创建 模型 garch(P,Q)，其中 P 是 GARCH 多项式的阶数， Q 是 ARCH 多项式的阶数。

创建 GARCH(3,2) 模型

garch(3,2)

创建具有已知系数的 GARCH 模型

创建一个具有平均偏移量的 GARCH(1,1) 模型，

yt=0.5+εt,

其中 εt=σtzt，

σ2t = 0.0001 + 0.75σ2t − 1 + 0.1ε2t − 1，

zt 是一个独立同分布的标准高斯过程。

 garh('Conant',00001,'GACH',0.75,...
    'AR H ,0.1,'Ofet'0.5)

---

---

访问 GARCH 模型属性

创建 garch 模型对象。

 garch(3,2)

GARCH 多项式有两个未知参数，分别对应滞后 1 和滞后 3。

显示扰动的分布。

Ditiuton

扰动是均值为 0 且方差为 1 的高斯扰动。

dl.Dirbton = trut('Nme','t','DF',5)

指定第一个滞后的 ARCH 系数为 0.2，第二个滞后的 ARCH 系数为 0.1。

ACH = {0.2 0.1}

要估计残差的参数，您可以将Mdl 数据传递 给 estimate 指定的参数并将其用作等式约束。或者，您可以指定其余的参数值，然后通过将完全指定的模型分别传递给simulate 或 来模拟或预测 GARCH 模型的条件方差 forecast。

收益序列似乎具有非零条件平均偏移，并且似乎表现出波动聚集。也就是说，较早年份的变异性小于晚年的变异性。对于此示例，假设 GARCH(1,1) 模型适用于该序列。

创建 GARCH(1,1) 模型。默认情况下，条件平均偏移为零。要估计偏移量，请将其指定为 NaN。

garh('GCHags',1,'ARHLgs',1,'Ofst',Na);

将 GARCH(1,1) 模型拟合到数据。

eimae(dl,r);

EstMdl 是一个完全指定的 garch 模型对象。也就是说，它不包含 NaN 值。您可以通过使用 生成残差infer，然后对其进行分析来评估模型的充分性 。

要模拟条件方差或序列，请传递 EstMdl 到 simulate。

要预测分布，请 EstMdl 转到 forecast.

模拟 GARCH 模型观察序列和条件方差

从完全指定的garch 模型对象模拟条件方差或序列路径 。也就是说，从估计garch 模型或已知 garch 模型（您在其中指定所有参数值）进行模拟 。

加载 Data 数据集。

RN;

创建具有未知条件平均偏移量的 GARCH(1,1) 模型。将模型拟合到年度收益序列。

gach('GCHLgs',1,ARCLgs',1,Ofet',Na);
Est = esiae(Mnr);

从估计的 GARCH 模型模拟每个时期的 100 条条件方差和序列路径。

mOb = nul(n); % 样本大小（T）
nuths = 100;     % 要模拟的路径数
rg(1);             % 用于重现
[Vim,Sm] = simae(EMdl,nuOs,NumPts,umPts);

VSim 和 YSim 是 T-by- numPaths 矩阵。行对应一个采样周期，列对应一个模拟路径。

绘制模拟路径的平均值以及 97.5% 和 2.5% 的百分位数。将模拟统计数据与原始数据进行比较。

Var = men(Vim,2);
VSI = quntie(Vi,[0.025 0.975],2);
Ymar = man(YSm,2);
YCI = qatle(Sim,[0.025 0.975],2);
 
pot(ae,im,);
hld on;
h2 = plt(des,Viar);
h =plo(ats,VSiCI,
hld off;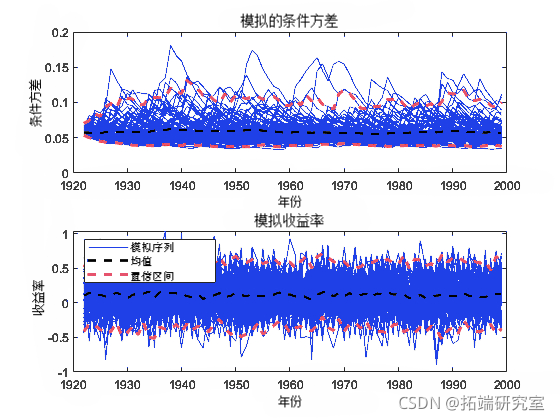

预测 GARCH 模型条件方差

从完全指定的garch 模型对象预测条件方差 。也就是说，根据估计garch 模型或garch 您指定所有参数值的已知 模型进行预测 。

加载 Data 数据集。

RN;

创建具有未知条件平均偏移量的 GARCH(1,1) 模型，并将该模型拟合到年度收益率序列。

dl = grh('GCas',1,'AHas',1,'Ofet',aN);
Edl = esate(dl,r);

使用估计的 GARCH 模型预测未来 10 年收益率序列的条件方差。将整个收益系列指定为样本前观察。软件使用样本前观测值和模型推断样本前条件方差。

numPeiods = 10;
F = foeast(EtMdl,uPes,nr);

绘制名义收益的预测条件方差。将预测与观察到的条件方差进行比较。

 
fgure;
pot(dtes);
hld n;
pot(dts(ed):ds(ed) + 10,[v(nd);vF]);

参考

[1] Tsay，金融时间序列的_RS 分析。第 3 版。John Wiley & Sons, Inc.，2010 年。