---

可下载资源

---

作者

此示例说明如何在变量之间存在复杂关系或单个变量来自不同分布时使用 copula 从多元分布生成数据。

copula 参数

近似置信区间

copula 参数的近似置信区间，以 1×2 标量值矩阵形式返回。第一列包含下边界，第二列包含上边界。默认情况下， fit 返回大约 95% 的置信区间。可以使用'Alpha' 名称-值对指定不同的置信区间 。

例子

将t  Copula拟合到股票收益数据

加载并绘制模拟股票收益数据。

hist(x,y)

---

---

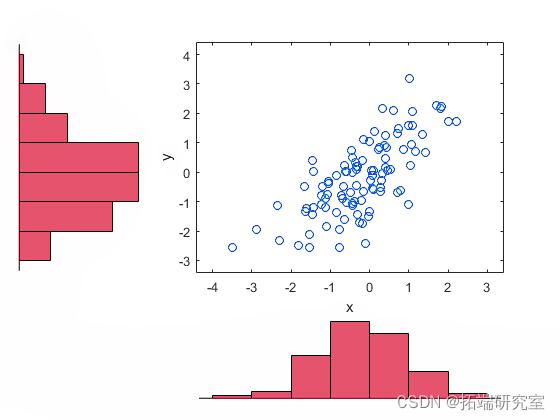
使用累积分布函数的核估计器将数据转换为 copula 。

density(x,x,'fuctin','cdf');

hist(u,v)

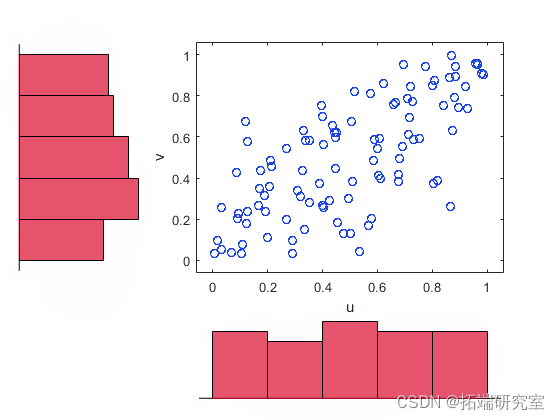
将_t_  copula拟合 到数据中。

rng default  % 方便重现
fit('t',\[u v\]'ppomaeML')

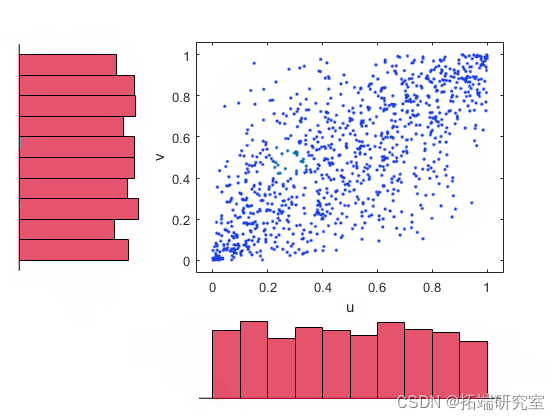
将随机样本变换回数据的原始量纲。

figure;
scterhst(x1,y1)

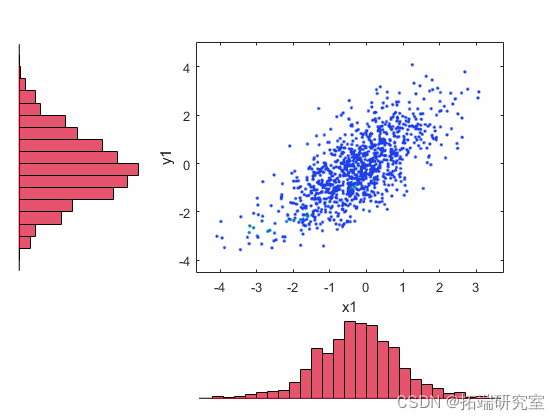
使用 Copulas 模拟相关随机变量

仿真输入之间的相关性

Monte-Carlo 模拟的设计决策之一是选择随机输入的概率分布。为每个单独的变量选择分布通常很简单，但决定输入之间应该存在什么依赖关系可能不是。理想情况下，模拟的输入数据应反映所建模的实际数量之间的相关性的已知信息。但是，在模拟中可能没有或几乎没有信息可用于建立任何依赖关系，在这种情况下，最好尝试不同的可能性，以确定模型的敏感性。

然而，当随机输入的分布不是标准多元分布时，可能很难实际生成具有相关性的随机输入。此外，一些标准的多元分布只能模拟非常有限的依赖类型。总是可以使输入独立，虽然这是一个简单的选择，但并不总是明智的，可能会导致错误的结论。

Ind = mvrn(\[0 0\], Simand, n);
XIn = exp(ZId);

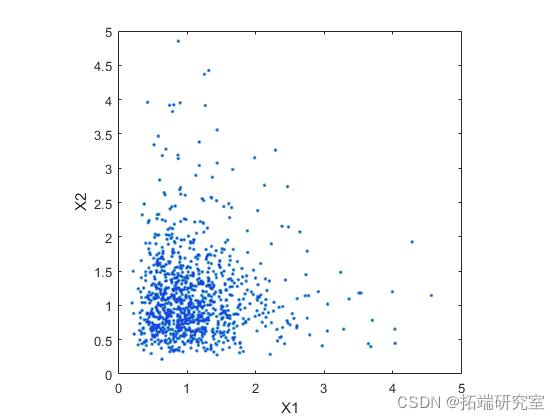
使用具有非零非对角项的协方差矩阵也很容易生成相关的双变量对数正态 rv。

Simep = sga.^2 .* \[1 rho; rho 1\]

mvnrnd(\[0 0\], Siaep, n);

第二个散点图说明了这两个二元分布之间的差异。

plot(XDp,'.');
axis equal;

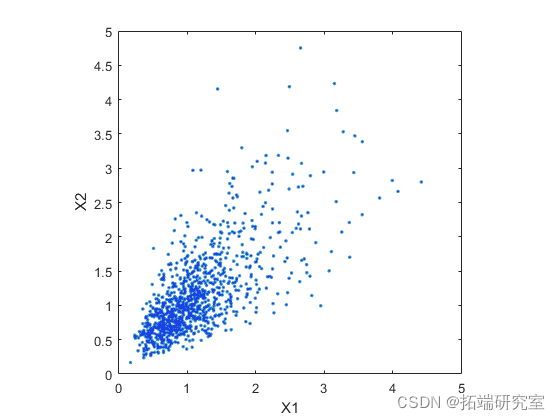
很明显，在第二个数据集中，X1 的大值与 X2 的大值相关联的趋势更大，对于小值也是如此。这种依赖性由基础双变量正态的相关参数 rho 确定。从模拟中得出的结论很可能取决于 X1 和 X2 是否具有相关性。

在这种情况下，二元对数正态分布是一个简单的解决方案，当然很容易推广到更高维度和边缘分布是 不同 对数正态的情况。还存在其他多元分布，例如，多元 t 和 Dirichlet 分布分别用于模拟相关的 t 和 beta 随机变量。但是简单的多元分布的列表并不长，它们仅适用于边缘都在同一族（甚至完全相同的分布）中的情况。在许多情况下，这可能是一个真正的限制。

构建相依双变量分布的更通用方法

尽管创建二元对数正态的上述构造很简单，但它用于说明更普遍适用的方法。首先，我们从二元正态分布生成值对。这两个变量之间存在统计相关性，且均具有正态边缘分布。接下来，对每个变量分别应用转换（指数函数），将边缘分布更改为对数正态分布。转换后的变量仍然具有统计相关性。

如果可以找到合适的转换，则可以推广此方法以创建具有其他边缘分布的相关双变量随机向量。事实上，确实存在构造这种变换的通用方法，尽管不像取幂那么简单。

根据定义，将正态 CDF（此处由 PHI 表示）应用于标准正态随机变量会导致在区间 [0, 1] 上均匀的 rv。要看到这一点，如果 Z 具有标准正态分布，则 U = PHI(Z) 的 CDF 为

  Pr{U <= u0} = Pr{PHI(Z) <= u0} = Pr{Z <= PHI^(-1)(u0)} = u0，

这是一些模拟的正常值和转换值的 U(0,1) rv 直方图的 CDF 证明了这一事实。

hist(z);

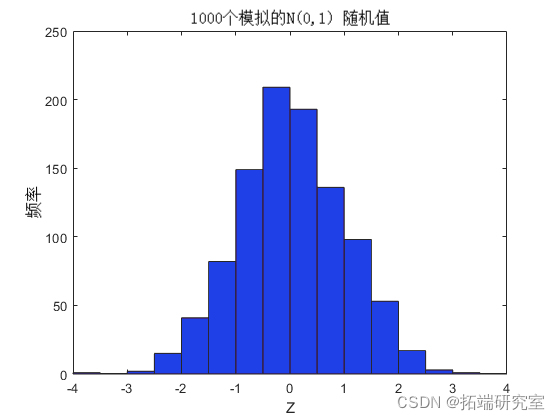
u = normcdf(z);

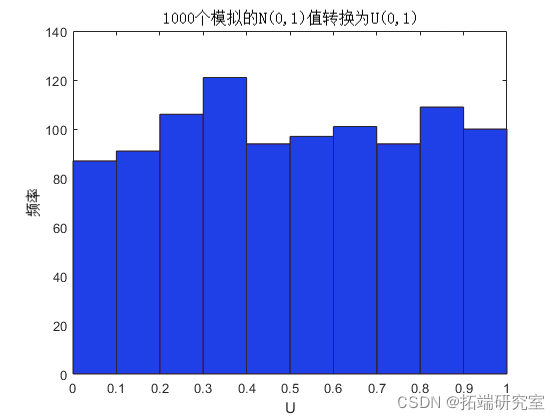
现在，借用单变量随机数生成理论，将任何分布 F 的逆 CDF 应用于 U(0,1) 随机变量会产生一个 rv，其分布正好是 F。这被称为反演方法。该证明本质上与上述前向情况的证明相反。另一个直方图说明了向伽马分布的转换。

gaminv(u,2,1);

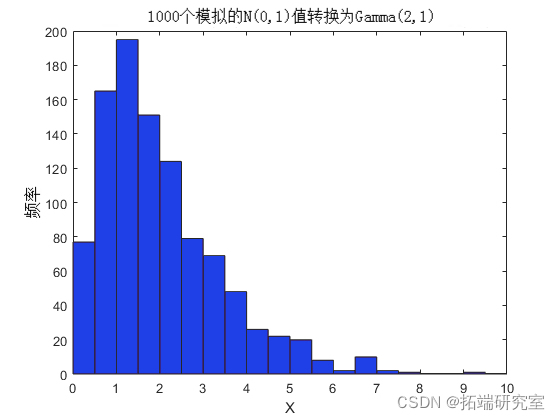
这种两步变换可以应用于标准双变量正态的每个变量，创建具有任意边缘分布的相关 rv。因为转换分别作用于每个成分，所以两个结果 rv 甚至不需要具有相同的边缘分布。变换定义为

  Z = \[Z1 Z2\] ~ N(\[0 0\],\[1 rho; rho 1\])
  U = \[PHI(Z1) PHI(Z2)\]
  X = \[G1(U1) G2(U2)\]

其中 G1 和 G2 是两个可能不同分布的逆 CDF。例如，我们可以从具有 t(5) 和 Gamma(2,1) 边缘的二元分布生成随机向量。

 nocf(Z);
 \[gav(U(:,1),2,1) tin(U(:,2),5)\];

该图在散点图旁边有直方图，以显示边缘分布和相关性。

hist(X);

plot(X,'.');

bar(ct1,-1,1);

等级相关系数

此构造中 X1 和 X2 之间的相关性由基础双变量正态的相关参数 rho 确定。但是， X1 和 X2 的线性相关性是 rho是 不正确的。例如，在原始对数正态情况下，该相关有一个形式：

  cor(X1,X2) = (exp(rho.*sigma.^2) - 1) ./ (exp(sigma.^2) - 1)

除非 rho 恰好是 1，否则它严格小于 rho。但是，在更一般的情况下，例如上面的 Gamma/t 构造，X1 和 X2 之间的线性相关性很难或不可能用 rho 表示，但可以使用模拟来表明发生了相同的效果。

那是因为线性相关系数表示 rv 之间的 _线性_相关性，并且当对这些 rv 应用非线性变换时，不会保留线性相关性。相反，秩相关系数（例如 Kendall’s tau 或 Spearman’s rho）更合适。

粗略地说，这些等级相关性衡量一个 rv 的大值或小值与另一个 rv 的大值或小值相关联的程度。然而，与线性相关系数不同，它们仅根据等级来衡量关联。因此，在任何单调变换下都保留了等级相关性。特别是，刚刚描述的变换方法保留了等级相关性。因此，知道双变量正态 Z 的秩相关准确地确定了最终变换后的 rv 的 X 的秩相关。 虽然仍然需要 rho 来参数化潜在的双变量正态，但 Kendall 的 tau 或 Spearman 的 rho 在描述 rv 之间的相关性时更有用，因为它们对于边缘分布的选择是不变的。

事实证明，对于二元正态分布，Kendall’s tau 或 Spearman’s rho 与线性相关系数 rho 之间存在简单的 1-1 映射：
subplot(1,1,1); plot(rho,ta);

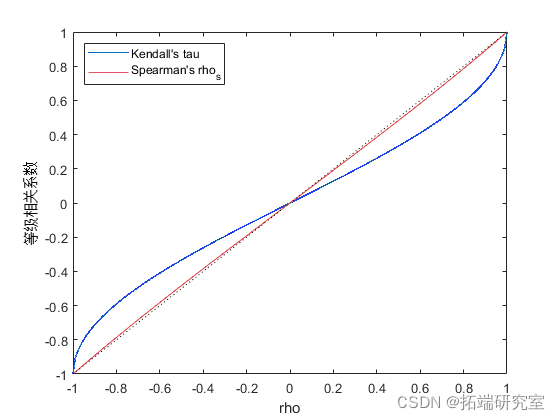
因此，通过为 Z1 和 Z2 之间的线性相关选择正确的 rho 参数值，很容易在 X1 和 X2 之间创建所需的秩相关，而不管它们的边缘分布如何。

请注意，对于多元正态分布，Spearman 的秩相关几乎与线性相关相同。然而，一旦我们转换为最终的随机变量，情况就不是这样了。

copula

上述构造的第一步定义了所谓的 copula，特别是高斯 copula。双变量 copula 只是两个随机变量的概率分布，每个变量的边缘分布都是均匀的。这两个变量可能是完全独立的、确定性相关的（例如，U2 = U1），或者介于两者之间。二元高斯 copulas 族由 Rho = [1 rho; rho 1]，线性相关矩阵。当 rho 接近 +/- 1 时，U1 和 U2 接近线性相关，当 rho 接近零时接近完全独立。

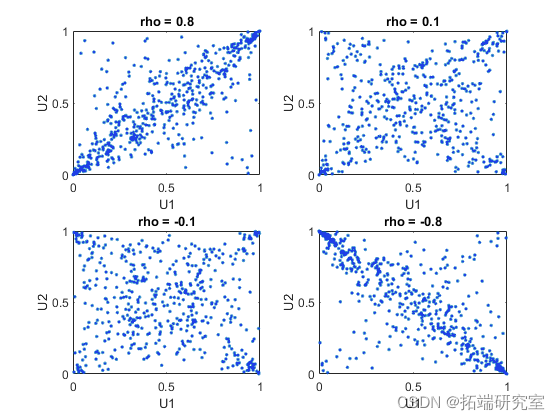
不同水平 rho 的一些模拟随机值的散点图说明了高斯 copula 的不同可能性范围：

U = nrf(Z,0,1);
plt(U,'.');

Z = vrd(\[0 0\], n);
U = ncf(Z,0,1);

plt(U,'.');

Z = mnd(\[0 0\], n);
U = nrcf(Z,0,1);
plt(U,'.');

Z = mrd(\[0 0\], n);
U = nocdf(Z,0,1);
plt(U,'.');

U1 和 U2 之间的相关性与 X1 = G(U1) 和 X2 = G(U2) 的边缘分布完全分开。X1 和 X2 可以被赋予 任何 边缘分布，并且仍然具有相同的秩相关。这是 copula 的主要吸引力之一——它们允许对依赖性和边缘分布进行这种单独的规范。

t Copulas

可以通过从二元 t 分布开始并使用相应的 t CDF 进行转换来构建不同的 copula 族。二元 t 分布使用 Rho（线性相关矩阵）和 nu（自由度）进行参数化。因此，例如，我们可以说 at(1) 或 at(5) copula，分别基于具有 1 个和 5 个自由度的多元变量 t。

不同水平 rho 的一些模拟随机值的散点图说明了 t(1) copulas 的不同可能性范围：

T = mvd(, nu, n);
U = tcf(T,nu);
plot(U);

T = mvtn( nu, n);

plot(U);

t copula 对 U1 和 U2 具有均匀的边缘分布，就像高斯 copula 一样。at copula 中成分之间的秩相关 tau 或 rho_s 也是与高斯函数相同的 rho 函数。然而，正如这些图所示，at(1) copula 与高斯 copula 有很大不同，即使它们的成分具有相同的等级相关性。不同之处在于它们的依赖结构。毫不奇怪，随着自由度参数 nu 变大，at(nu) copula 接近相应的高斯 copula。

与高斯 copula 一样，可以在 copula 上施加任何边缘分布。例如，使用具有 1 个自由度的 copula，我们可以再次从具有 Gam(2,1) 和 t(5) 边缘的二元分布生成随机向量：

\[n1,cr\] = hist(X(:,1);
\[n2,c2\] = hist(X(:,2));

plot(X,'.');

h1 = gca;

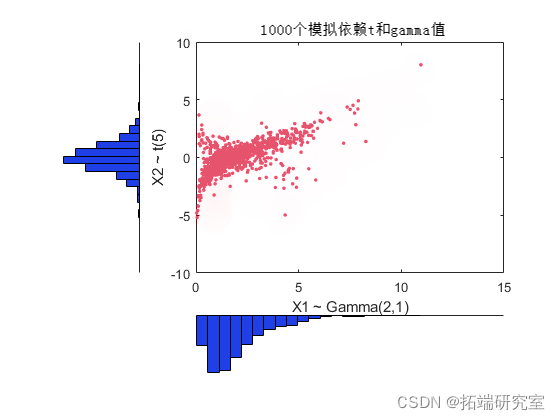
与之前构建的基于高斯 copula 的双变量 Gamma/t 分布相比，这里基于 at(1) copula 构建的分布具有相同的边缘分布和相同的变量之间的秩相关，但依赖性却大不相同结构体。这说明了一个事实，即多元分布并不是由它们的边缘分布或它们的相关性唯一定义的。应用程序中特定 copula 的选择可能基于实际观察到的数据，或者可以使用不同的 copula 来确定模拟结果对输入分布的敏感性。

高维 Copulas

Gaussian 和 t copula 被称为椭圆 copula。很容易将椭圆 copula 推广到更多维度。例如，我们可以使用 Gaussian copula 模拟来自具有 Gamma(2,1)、Beta(2,2) 和 t(5) 边缘的三变量分布的数据，如下所示。

X = \[gaminv betainv tinv(U)\];
plot3(X,'.');

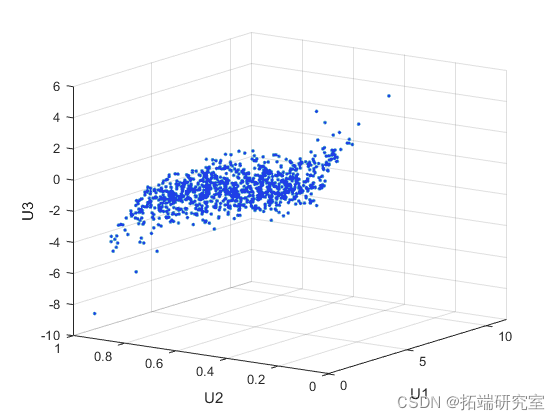
请注意，线性相关参数 rho 与例如 Kendall tau 之间的关系对于此处使用的相关矩阵 Rho 中的每个条目都成立。我们可以验证数据的样本秩相关近似等于理论值。

 corr(X, 'type','Kendall')

Copulas 和经验边缘分布

为了使用 copula 模拟相关的多元数据，我们已经看到我们需要指定

  1) copula 族（和任何形状参数），
  2) 变量之间的秩相关，以及
  3) 每个变量的边缘分布

假设我们有两组股票收益数据，我们想运行蒙特卡罗模拟，输入与我们的数据遵循相同的分布。

size(sos,1);
hist(stos(:,1),10);

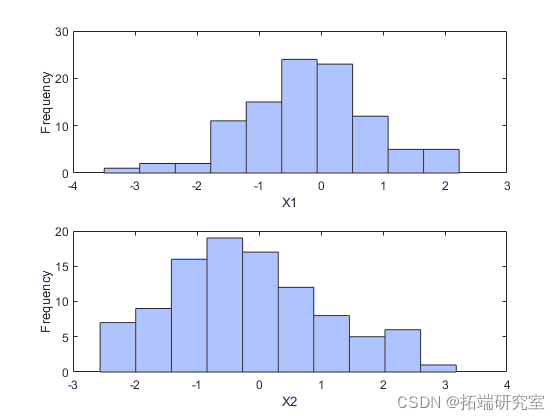
（这两个数据向量具有相同的长度，但这并不重要。）

我们可以为每个数据集分别拟合一个参数模型，并将这些估计值用作我们的边缘分布。但是，参数模型可能不够灵活。相反，我们可以对边缘分布使用经验模型。我们只需要一种方法来计算逆 CDF。

这些数据集的经验逆 CDF 只是一个阶梯函数，步长为 1/nobs、2/nobs、… 1。步长只是排序后的数据。

stairs(inCF1);

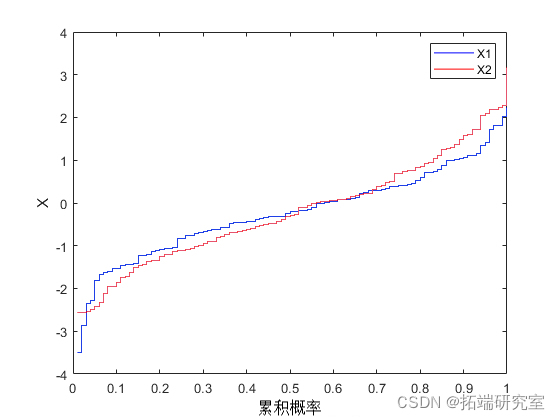
对于模拟，我们可能想要尝试不同的联结和相关性。在这里，我们将使用具有相当大的负相关参数的二元 t(5) copula。

tcdf(T,nu);
\[inCDF1 inCDF2\];

plot(X(:,1),X(:,2),'.');

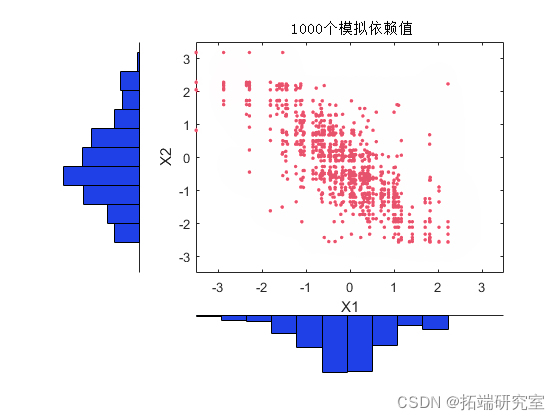
模拟数据的边缘直方图与原始数据的边缘直方图非常匹配，并且随着我们模拟更多对值而变得相同。请注意，这些值是从原始数据中提取的，并且由于每个数据集中只有 100 个观测值，因此模拟数据有些“离散”。克服此问题的一种方法是向最终模拟值添加少量随机变化（可能为正态分布）。这等效于使用经验逆 CDF 的平滑版本。