在此数据集中,我们必须预测信贷的违约支付,并找出哪些变量是违约支付的最强预测因子?
以及不同人口统计学变量的类别,拖欠还款的概率如何变化?
有25个变量:
思路:提升方法基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合得出的判断要比其中任何一个专家单独的判断都好。也就是”三个臭皮匠,顶个诸葛亮”。
理论支持:在PAC(probably approximately correct)框架中,一个概念(类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的;一个概念,如果存在一个多项式学习算法能够学习它,学习的正确率仅比随机猜测好一点,那么就成这个概念是弱可学习的。
后来Schapire证明强可学习与弱可学习是等价的。也就是说,在PAC框架下,一个概念是强可学习的充要条件是这个概念是弱可学习。
综上我们可以通过集成一系列弱学习器来得到一个强学习器。
而发现一个弱学习算法比发现一个强学习算法容易的多。因此我们找到了一条曲线救国的路线:低成本得到多个弱学习算法,再通过组合这些弱学习算法将其提升成一个强学习算法。而具体如何进行提升就是我们需要解决的问题。
对于分类问题而言,给定一个训练样本集合,发现粗糙分类规则(弱分类器)比发现精确分类规则(强分类器)要容易的多。提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器,然后组合这些分类器,构成一个强分类器。大多数提升方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用若学习算法学习一系列弱分类器。
1. ID: 每个客户的ID
2. LIMIT_BAL: 金额
3. SEX: 性别(1 =男,2 =女)
4.教育程度:(1 =研究生,2 =本科,3 =高中,4 =其他,5 =未知)
5.婚姻: 婚姻状况(1 =已婚,2 =单身,3 =其他)
6.年龄:
7. PAY_0: 2005年9月的还款状态(-1 =正常付款,1 =延迟一个月的付款,2 =延迟两个月的付款,8 =延迟八个月的付款,9 =延迟9个月以上的付款)
8. PAY_2: 2005年8月的还款状态(与上述相同)
9. PAY_3: 2005年7月的还款状态(与上述相同)
10. PAY_4: 2005年6月的还款状态(与上述相同)
11. PAY_5: 2005年5月的还款状态(与上述相同)
12. PAY_6: 还款状态2005年4月 的账单(与上述相同)
13. BILL_AMT1: 2005年9月的账单金额
14. BILL_AMT2: 2005年8月的账单金额
15. BILL_AMT3: 账单金额2005年7月 的账单金额
16. BILL_AMT4: 2005年6月的账单金额
17. BILL_AMT5: 2005年5月的账单金额
18. BILL_AMT6: 2005年4月
19. PAY_AMT1 2005年9月,先前支付金额
20. PAY_AMT2 2005年8月,以前支付的金额
21. PAY_AMT3: 2005年7月的先前付款
22. PAY_AMT4: 2005年6月的先前付款
23. PAY_AMT5: 2005年5月的先前付款
24. PAY_AMT6: 先前的付款额在2005年4月
25. default.payment.next.month: 默认付款(1 =是,0 =否)
现在,我们知道了数据集的整体结构。因此,让我们应用在应用机器学习模型时通常应该执行的一些步骤。
第1步:导入
import numpy as np import matplotlib.pyplot as plt
所有写入当前目录的结果都保存为输出。
dataset = pd.read_csv('Card.csv')
现在让我们看看数据是什么样的
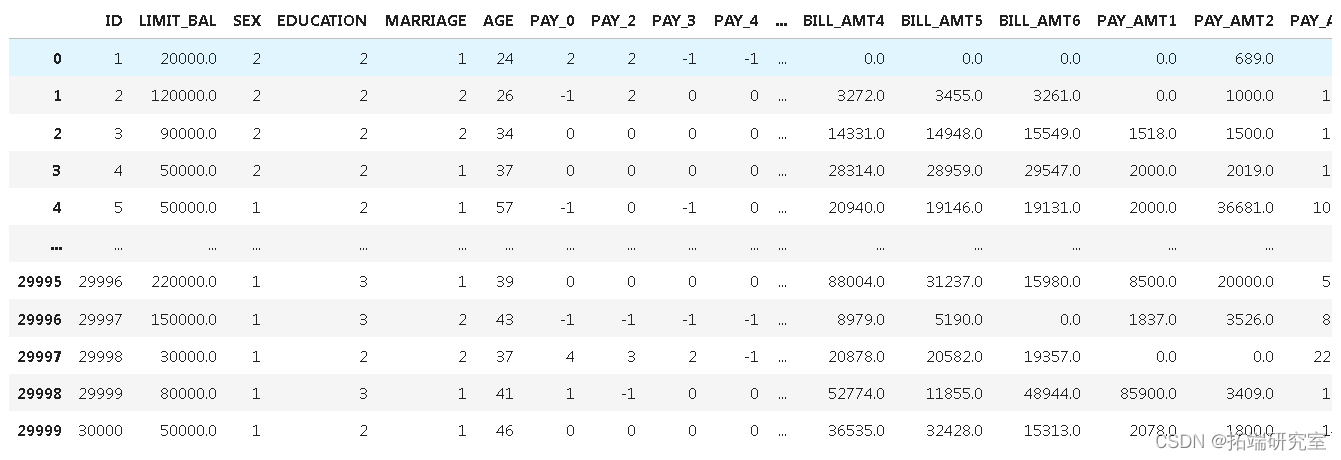
第2步:数据预处理和清理
dataset.shape
(30000, 25)
意味着有30,000条目包含25列
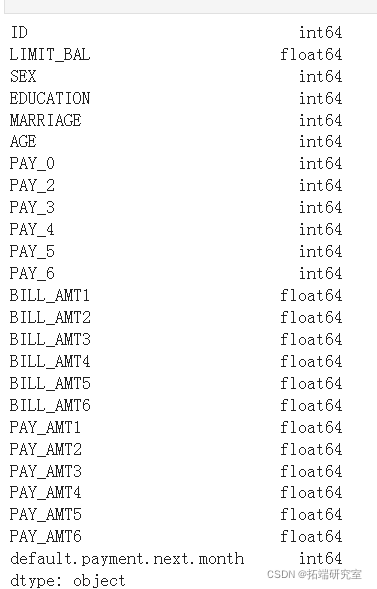
从上面的输出中可以明显看出,任何列中都没有对象类型不匹配。
#检查数据中Null项的数量,按列计算。 dataset.isnull().sum()
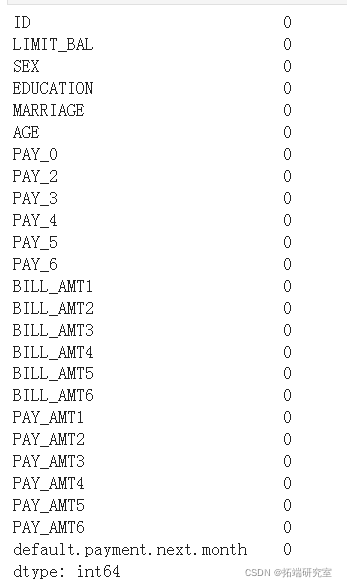
步骤3.数据可视化和探索性数据分析
# 按性别检查违约者和非违约者的计数数量 sns.countplot
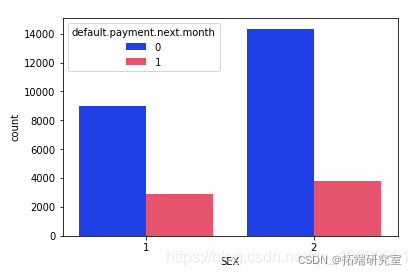
从上面的输出中可以明显看出,与男性相比,女性的整体拖欠付款更少
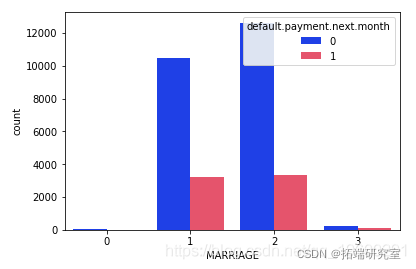
可以明显看出,那些拥有婚姻状况的人的已婚状态人的默认拖欠付款较少。
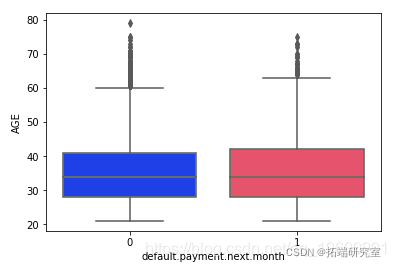
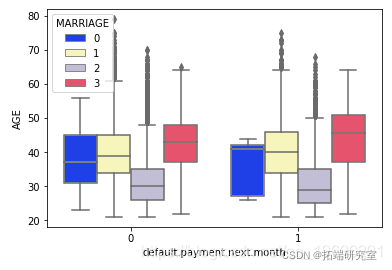
sns.pairplot

sns.jointplot
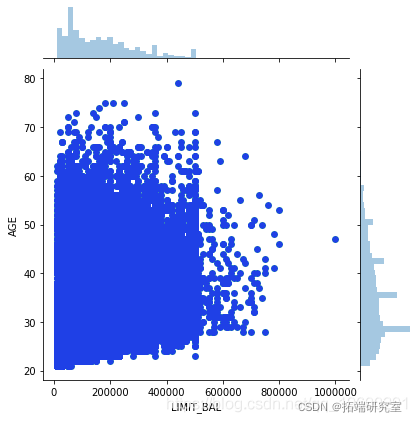
男女按年龄分布
g.map(plt.hist,'AGE')
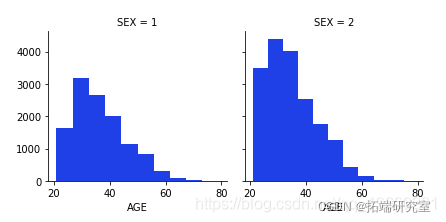
dataset\['LIMIT_BAL'\].plot.density
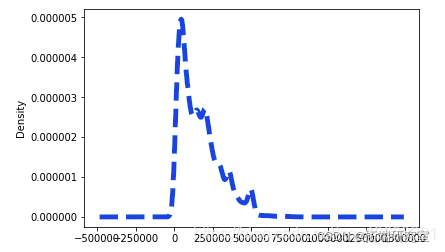
步骤4.找到相关性
X.corrwith
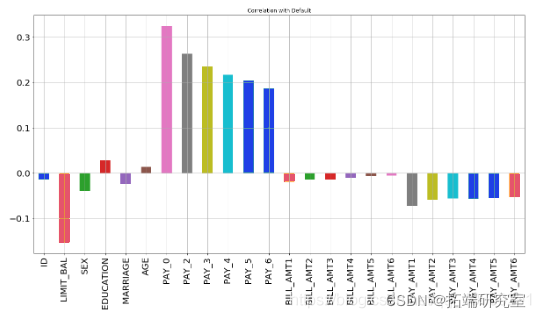
从上图可以看出,最负相关的特征是LIMIT_BAL,但我们不能盲目地删除此特征,因为根据我的看法,这对预测非常重要。ID无关紧要,并且在预测中没有任何作用,因此我们稍后将其删除。
随时关注您喜欢的主题
# 绘制热图 sns.heatmap(corr)
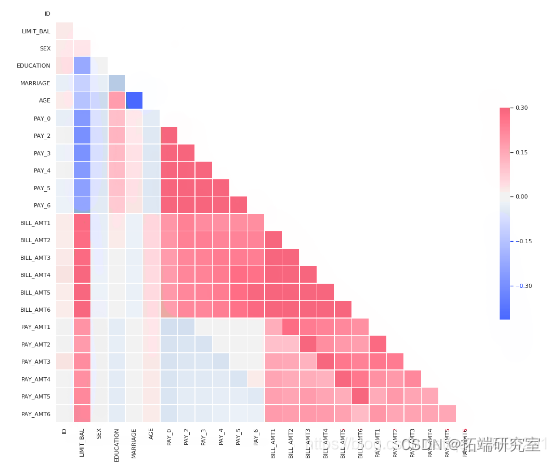
步骤5:将数据分割为训练和测试集
训练数据集和测试数据集必须相似,通常具有相同的预测变量或变量。它们在变量的观察值和特定值上有所不同。如果将模型拟合到训练数据集上,则将隐式地最小化误差。拟合模型为训练数据集提供了良好的预测。然后,您可以在测试数据集上测试模型。如果模型在测试数据集上也预测良好,则您将更有信心。因为测试数据集与训练数据集相似,但模型既不相同也不相同。这意味着该模型在真实意义上转移了预测或学习。
因此,通过将数据集划分为训练和测试子集,我们可以有效地测量训练后的模型,因为它以前从未看到过测试数据,因此可以防止过度拟合。
我只是将数据集拆分为20%的测试数据,其余80%将用于训练模型。
train\_test\_split(X, y, test\_size = 0.2, random\_state = 0)
步骤6:规范化数据:特征标准化
对于许多机器学习算法而言,通过标准化(或Z分数标准化)进行特征标准化可能是重要的预处理步骤。
许多算法(例如SVM,K近邻算法和逻辑回归)都需要对特征进行规范化,
min\_test = X\_test.min() range\_test = (X\_test - min_test).max() X\_test\_scaled = (X\_test - min\_test)/range_test
步骤7:应用机器学习模型
from sklearn.ensemble import AdaBoostClassifier adaboost =AdaBoostClassifier()

xgb\_classifier.fit(X\_train\_scaled, y\_train,verbose=True) end=time() train\_time\_xgb=end-start
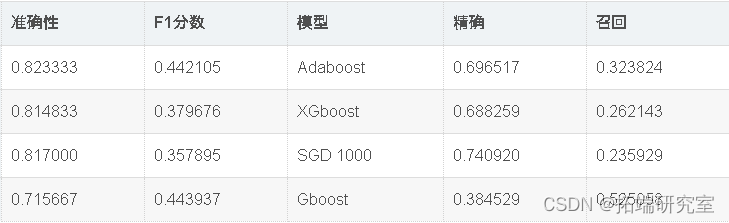
应用具有100棵树和标准熵的随机森林
classifier = RandomForestClassifier(random_state = 47, criterion = 'entropy',n_estimators=100)

svc_model = SVC(kernel='rbf', gamma=0.1,C=100)
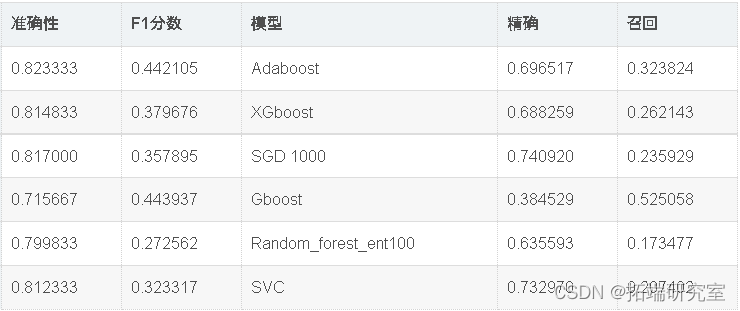
knn = KNeighborsClassifier(n_neighbors = 7)
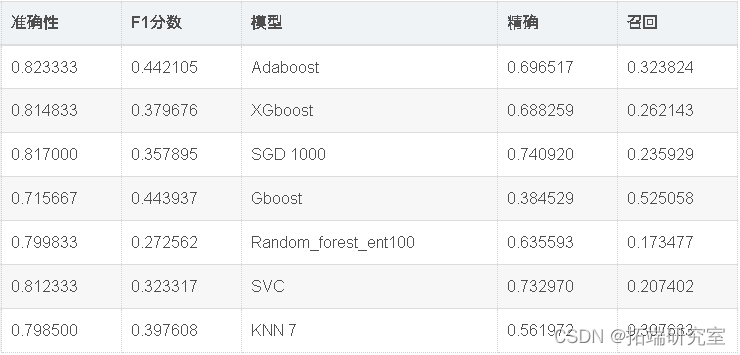
步骤8:分析和比较机器学习模型的训练时间
Train_Time = \[ train\_time\_ada, train\_time\_xgb, train\_time\_sgd, train\_time\_svc, train\_time\_g, train\_time\_r100, train\_time\_knn \]
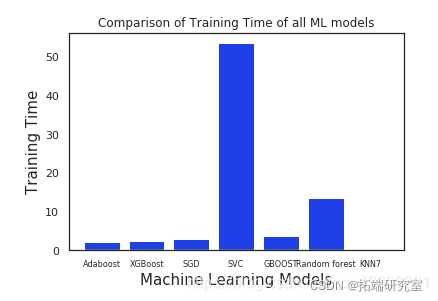
从上图可以明显看出,与其他模型相比,Adaboost和XGboost花费的时间少得多,而其他模型由于SVC花费了最多的时间,原因可能是我们已经将一些关键参数传递给了SVC。
步骤9.模型优化
在每个迭代次数上,随机搜索的性能均优于网格搜索。同样,随机搜索似乎比网格搜索更快地收敛到最佳状态,这意味着迭代次数更少的随机搜索与迭代次数更多的网格搜索相当。
在高维参数空间中,由于点变得更稀疏,因此在相同的迭代中,网格搜索的性能会下降。同样常见的是,超参数之一对于找到最佳超参数并不重要,在这种情况下,网格搜索浪费了很多迭代,而随机搜索却没有浪费任何迭代。
现在,我们将使用Randomsearch cv优化模型准确性。如上表所示,Adaboost在该数据集中表现最佳。因此,我们将尝试通过微调adaboost和SVC的超参数来进一步优化它们。
参数调整
现在,让我们看看adaboost的最佳参数是什么
random\_search.best\_params_
{'random\_state': 47, 'n\_estimators': 50, 'learning_rate': 0.01}

random\_search.best\_params_
{'n\_estimators': 50, 'min\_child\_weight': 4, 'max\_depth': 3}

random\_search.best\_params_
{'penalty': 'l2', 'n\_jobs': -1, 'n\_iter': 1000, 'loss': 'log', 'alpha': 0.0001}
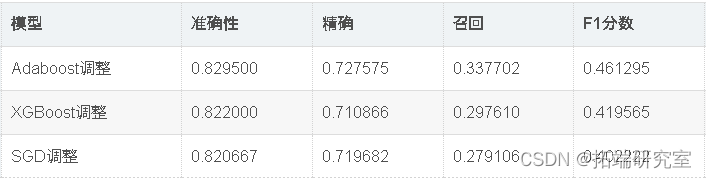
出色的所有指标参数准确性,F1分数精度,ROC,三个模型adaboost,XGBoost和SGD的召回率现已优化。此外,我们还可以尝试使用其他参数组合来查看是否会有进一步的改进。
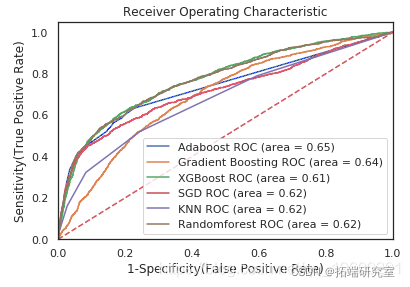
ROC曲线图
auc = metrics.roc\_auc\_score(y\_test,model.predict(X\_test_scaled)) plt.plot(\[0, 1\], \[0, 1\],'r--')
# 计算测试集分数的平均值和标准差 test_mean = np.mean # 绘制训练集和测试集的平均准确度得分 plt.plot # 绘制训练集和测试集的准确度。 plt.fill_between
如果树的数量在10左右,则该模型存在高偏差。两个分数非常接近,但是两个分数都离可接受的水平太远,因此我认为这是一个高度偏见的问题。换句话说,该模型不适合。
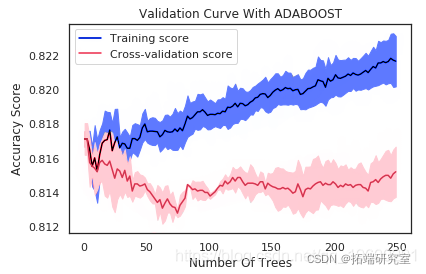
验证曲线的解释
在最大树数为250的情况下,由于训练得分为0.82但验证得分约为0.81,因此模型存在高方差。换句话说,模型过度拟合。同样,数据点显示出一种优美的曲线。但是,我们的模型使用非常复杂的曲线来尽可能接近每个数据点。因此,具有高方差的模型具有非常低的偏差,因为它几乎没有假设数据。实际上,它对数据的适应性太大。
从曲线中可以看出,大约30到40的最大树可以最好地概括看不见的数据。随着最大树的增加,偏差变小,方差变大。我们应该保持两者之间的平衡。在30到40棵树的数量之后,训练得分就开始上升,而验证得分开始下降,因此我开始遭受过度拟合的困扰。因此,这是为什么30至40之间的任何数量的树都是一个不错的选择的原因。
结论
因此,我们已经看到,调整后的Adaboost的准确性约为82.95%,并且在所有其他性能指标(例如F1分数,Precision,ROC和Recall)中也取得了不错的成绩。
此外,我们还可以通过使用Randomsearch或Gridsearch进行模型优化,以找到合适的参数以提高模型的准确性。
我认为,如果对这三个模型进行了适当的调整,它们的性能都会更好。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 【梯度提升专题】XGBoost、Adaboost、CatBoost预测合集:抗乳腺癌药物优化、信贷风控、比特币应用|附数据代码
【梯度提升专题】XGBoost、Adaboost、CatBoost预测合集:抗乳腺癌药物优化、信贷风控、比特币应用|附数据代码 银行信贷风控专题:Python、R 语言机器学习数据挖掘应用实例合集:xgboost、决策树、随机森林、贝叶斯等
银行信贷风控专题:Python、R 语言机器学习数据挖掘应用实例合集:xgboost、决策树、随机森林、贝叶斯等 Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据:旅游市场差异、价格预测
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据:旅游市场差异、价格预测 SMOTEBoost、RB-Boost和RUS-Boost不平衡数据集的集成分类器分析酵母数据集、治疗乳腺癌候选药物筛选|附数据代码
SMOTEBoost、RB-Boost和RUS-Boost不平衡数据集的集成分类器分析酵母数据集、治疗乳腺癌候选药物筛选|附数据代码


