配对交易提出的问题之一是股票的贝塔值相对于市场的不稳定估计。
这是一个可能的解决方案的建议，这并不是真正的解决方案。
看看下图：
可下载资源
收缩 “Shrinkage”，是指在包含随机效应的模型中，由模型可以估计得到随机效应的标准偏差值(ω)，另外由模型和观测值还可通过贝叶斯反馈（Empirical Bayes (“post hoc”) estimates (EBEs)）估计得到具体的每一个个体(i)的个体参数的值ηEBE，然后对所有ηi进行描述性统计可以得到SD(η)，则该随机效应的参数值的收缩值计算公式为：
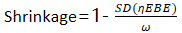
收缩值可以反应当前数据所包含的信息是否足以支持对于该随机效应估计，越小越好，当收缩值过大时，提示当前数据并不足以估计该随机效应，由该随机效应所预测的EBE个体值也是失真的，不能发挥诊断和协变量搜索的作用。
一般：
Shrinkage的值在0~1之间，
-
当Shrinkage取负值时，则提示经验贝叶斯估计的参数分布方差比估计的方差值大，模型对该随机效应的方差指定可能存在错误。
-
越接近0表示收缩值越好，没有金标准的接受标准，但一般认为小于20~30%以下是可以接受的，
-
当高于30%则提示当前的数据不足以支持估计该参数的个体间变异，与之相关的诊断图表不能够正确的显示诊断信息，不能用用于诊断；较大的收缩值并不能有用于指示当前的模型是否被错误指定，即使是正确的模型依然可能会遇到收缩值较大的情况。
-
当收缩值较大时，表示经验贝叶斯估计的个体参数的分布方差比模型估计的方差小，此时的个体参数不能很好的符合模型估计的分布，而表现出更加集中的分布，极端情况，当EBEs估计的参数方差为0即，Shrinkage=1时，EBEs估计的参数都是群体典型值。
-
当该随机效应估计得到的方差很小，收缩值很大时，提示当前的数据不足以估计该参数的随机效应，可取消对改参数的随机效应的估计，即不估计改参数的随机效应。
Microsoft的滚动系数（回归：MSFT~SPY）- 120 天的窗口，纯蓝色是使用完整样本估计的 beta
我们可以看到截距并没有太大的波动，这确实意味着如果市场不波动，MSFT 也不会。
然而，beta在稳定的市场（贝塔 = 1）和中性（贝塔 = 0）之间波动。
当然，随着窗口的缩短，事情会变得更加不稳定，120 天大致意味着最近的 6 个月，这并不短。
也许我们可以在长期（稳定）估计和短期估计之间找到一个折衷方案。
一种方法是简单地平均两个估计值。另一种是使用收缩估计的方式对它们进行平均。
但现在，这种方法的一个简单解释是平均计算 X 矩阵中的离散度，在我们的例子中，它只是市场收益和截距，当前周期是否波动？可以使用 X 矩阵的奇异值分解来给出解释。
我们得到一个新的 beta 估计值，它是短期和长期估计值的平均值。我们需要决定应用多少收缩。
我们有一个参数，称为超参数，它决定了要应用的收缩量，低数字意味着对长期估计的拉动较小，而一个高的数字意味着对长期的拉动较大，因此对短期估计的权重较小。结果是：
你可以看到，你应用的缩减量越大，估计值就越接近它的长期值。将超参数取为0.1将防止β值波动到负值区域，但仍为可能的结构性变化留出一些空间。
你可以用这个方案来调和不稳定的估计程序和常识性的论点，例如，可能在这段时间内β值确实是负的，但这有意义吗？ 可能你的估计值变成负的，只是因为你想允许结构性变化，这是一件好事，这导致了 “不那么直观 “的估计。
以下代码包含一个函数，用于绘制您自己的数据，将希望查看的时间范围、窗口长度和股票代码作为输入。
ret <<- matrix # 收益矩阵
for (i in 1:l){
dat0 = (getSymbols
ret<<- dat - 1
}
for (i in 1:(n-w)){
bet0\[i\] = lm
bet1\[i\] = lm
}
btt <<- lm$coef\[2\] # 我们以后需要它作为一个先验平均数
plot
abline
legend
plotbe
Aok <- 0.01 #又称正则化参数
A = Amoink*diag(2)
# 你可以尝试用不同的值来代替对角线
# 也许你不想在另一个应用程序中缩小截距
prbeta
随时关注您喜欢的主题
poet = matrix
for (i in 2:(n-wl)){
bet0\[i\] = lm$coef\[1\]
bet1\[i\] = lm$coef\[2\]
x = cbind
post\[i,\] = solve
}
plot(postbet
lines注意：
这个想法与“岭回归”有关，也可以看作是一种半贝叶斯方法，其中先验的均值等于长期估计。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
