今年的收益是否真的与典型年份的预期不同？
差异实际上与典型年份的预期不同吗？这些都是相当容易回答的问题。
我们可以使用均值相等或方差相等的测试。但是下面这个问题呢。
置换检验的思路简单的说如下：
提出原假设，比如XX处理后结果没有变化
计算统计量，如两组的均值之差，记作t0
将所有样本放在一起，然后随机排序进行分组，再计算其统计量t1
重复第3步骤，直至所有排序可能性都齐全（比如有A组有n样本，B组有m样本，则总重复次数相当于从n+m中随机抽取n个的次数），得到一系列的统计量（t1-tn）
最后将这些统计量按照从小到大排序，构成抽样分布，再看t0是否落在分布的置信区间内（如95%置信区间），这时候可计算一个P值（如果抽样总体1000次统计量中大于t0的有10个，则估计的P值为10/1000=0.01），落在置信区间外则拒绝原假设
如果第3步骤是将所有可能性都计算了的话，则是精确检验；如果只取了计算了部分组合，则是近似结果，这时一般用蒙特卡罗模拟（Monte Carlo simulation）的方法进行置换检验
置换检验和参数检验都计算了统计量，但是前者是跟置换观测数据后获得的经验分布进行比较，后者则是跟理论分布进行比较
今年的收益概况与一般年份的预期情况是否不同？
这是一个更加普遍和重要的问题，因为它包括所有的时刻和尾部行为。而且它的答案也不那么简单。
我在想一定有一种方法可以正式检验收益密度之间的差异，而不仅仅是量化、可视化和用眼睛看。确实有这样的方法。这篇文章的目的是展示如何正式检验密度之间的平等。
事实上，至少有两种方法可以检验两个密度或两个分布之间的平等。第一种是比较经典的。这种检验被称为Kolmogorov-Smirnov检验。另一种是比较现代的，使用Permutation Test置换检验（需要模拟）。我们展示这两种方法。让我们先拉出一些价格数据。
end<- format(Sy.D, "%Y-%m-%d") l = lenh da0 <- lay Time <- index ret <- as.numeric/as.numeric -1 tail(rt) # 得到直到2018年的指数。 # 我们随后将2018年与其他年份进行比较 tid<- which(index)
# 每日收益的平均值和SD（2018年除外） > mean(100*rt\[1:pd\])
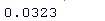
> SD(100*retd\[1:tid\])
> # 2008年（到目前为止）每日回报的平均值和SD值 > mean(100*rtd\[-c(1:tpd)\])
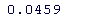
> SD(100*red\[-c(1:mid)\])
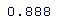
我们可以看到，2018 年每日收益的均值和标准差与其余的均值和标准差略有不同。这是估计密度的样子：
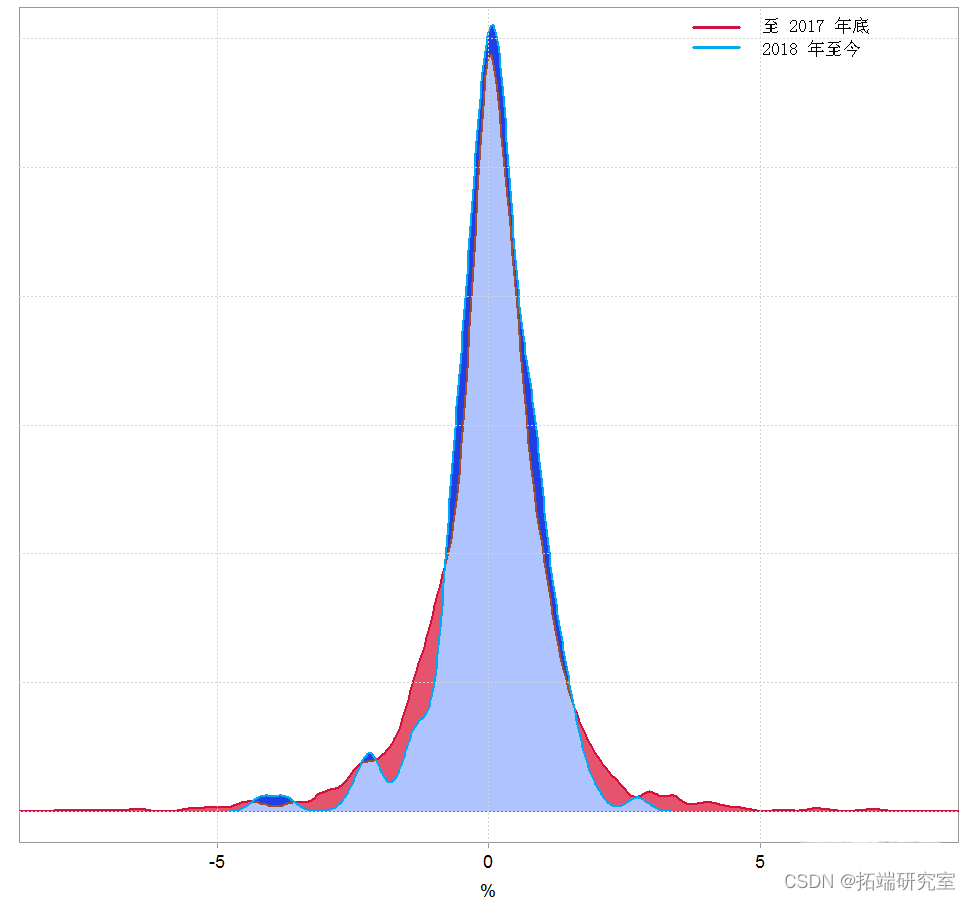
Kolmogorov-Smirnov 检验
我们可以做的是计算每个密度的累积分布函数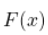
。2018年的那个和不包括2018年的那个。说
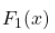分布是针对2018年的，
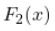分布是针对其他的。我们计算每个X的差异
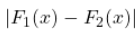。我们知道这些（绝对）差异的最大值是如何分布的，所以我们可以用这个最大值作为测试统计量，如果它在尾部的分布太远，我们就认为这两个分布是不同的。从形式上看。
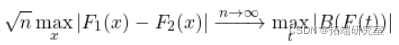
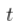介于 0 和 1 之间（通过构造，因为我们减去两个概率并取绝对值）。 
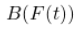是一个 Brownian bridge. （最大）差异具有已知分布。这是一个极限分布，所以我们需要大量的观测值 n 才能对这个检验有信心。
随时关注您喜欢的主题
Kolmogorov-Smirnov 测试 – R 代码
让我们将 2018 年的每日收益与其余收益进行比较，看看基于 Kolmogorov-Smirnov 检验的分布是否相同：
# Kolmogorov-Smirnov测试 #### ks.test
我们看到，最大值是0.067，根据极限分布，P值是0.3891。所以没有证据表明2018年的分布与其他的分布有任何不同。
让我们来看看置换检验。主要原因是，鉴于Kolmogorov-Smirnov 检验是基于极限分布的，为了使其有效，我们需要大量的观察结果。但是现在我们不必像过去那样依赖渐进法，因为我们可以使用计算机。
两个密度相等的置换检验Permutation Test
直观地说，如果密度完全相同，我们可以把它们放在一起，从 “捆绑数据 “中取样。在我们的例子中，因为我们把收益率聚集在一个向量中，对向量进行排列意味着2018年的每日收益率现在分散在向量中，所以像上面的方程那样取一个差值，就像从一个无效假设中进行模拟：2018年每日收益率的分布与其他的完全相同。现在，对于每个x，我们将有一个在原假设下的差异。我们也有每个x的实际差异，来自我们的观察数据。我们现在可以将密度之间的实际差异（每个x）平方（或取绝对值），并将其与我们从 “数据 “生成的模拟结果进行比较。通过观察实际差异落在模拟差异的哪个四分位数，可以估计出p值。
如果实际数据远远超出了原假设下的分布范围，那么我们将拒绝分布相同的假设。
密度比较置换检验 – R 代码
我们来执行刚刚描述的操作。两个参数 boot 和grid 是您想要的模拟数量以及您在计算 x 时想要使用的网格点数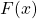 
. 因此 ngrid=100 。
# 我们需要两组的索引，2018年和其他的。 id <- substr tmnd <- i1 == 2018 sme
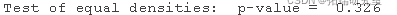
我们可以看到 p 值与我们使用 Kolmogorov-Smirnov 检验得到的值差别不大。这是它的样子：
等密度检验：p 值 = 0.326
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
BC变换的EWMA控制图对顺丰控股股票的分析研究
