多项式回归是独立x变量和因果y变量之间的非线性关系。
当我们分析有一些弯曲的波动数据时，拟合这种类型的回归是必不可少的。
在这篇文章中，我们将学习如何用多项式回归数据拟合曲线并在Python中绘制。我们在本教程中使用NumPy和matplotlib库。
可下载资源
我们将首先加载本教程所需的模块。
在许多实际问题分析中，回归分析的应用十分广泛，它是处理变量之间相关关系最常用的一种统计方法。回归分析可分为线性回归和非线性回归。
线性回归分析相信大家都已经非常熟悉了，它主要分析有线性回归趋势的两个变量间的关系。
但是在处理许多实际问题时，变量间的关系并非直线关系，例如细菌生长曲线、药物动力学、毒物剂量与动物死亡率的关系等等。此时，若采用线性回归分析将丢失大量信息，甚至得出错误结论。因此，就需要我们采用非线性回归模型来处理此类问题。
非线性回归有多种形式，包括双曲线、二次曲线、三次曲线、幂函数曲线、指数函数曲线、S形曲线、对数曲线、指数曲线等。
非线性回归分析的关键是确定函数的具体形式。通常需要根据科学研究或生产实际中的具体问题或试验数据的特征做出合适的选择。
import numpy as np
import matplotlib.pyplot as plt我们需要测试数据，我们可以按下图所示生成。你也可以使用你自己的数据集。
n = 250 # 元素数
train_x = np.array(x)
train_y = np.array(y)
我们将通过创建一个散点图来直观地检查x数据。
plt.scatter(train\_x, train\_y)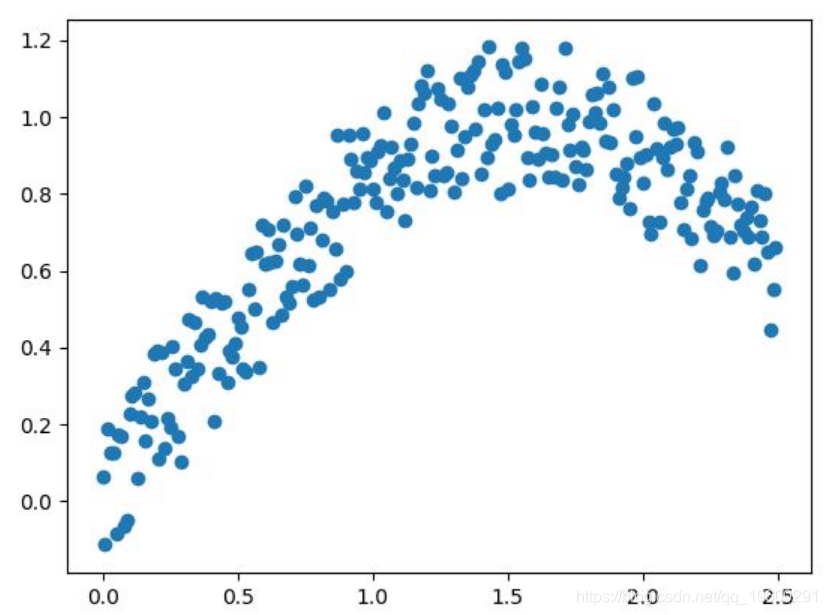
接下来，我们将用PolymonialFeatures类定义多项式模型，在训练数据上进行拟合。
fit\_transform(train\_x.reshape(-1, 1))我们需要一个线性模型，我们将定义它并在训练数据上拟合。然后我们用这个模型来预测x数据。
liniearModel.fit(xpol, train_y\[:,\])最后，我们将绘制出拟合的曲线。
plt.plot(train_x, polyfit, color = 'red')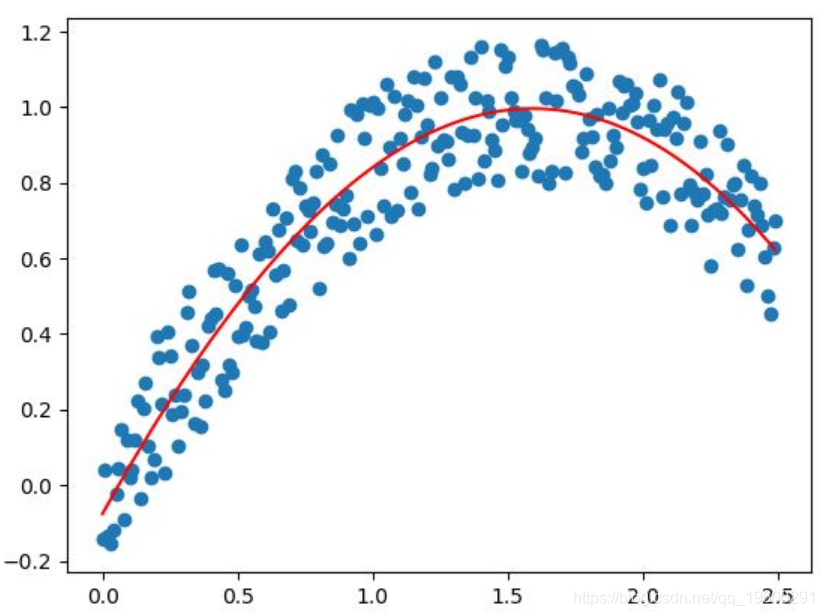
在这篇文章中，我们已经简单地了解了如何在Python中拟合多项式回归数据。
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
