我们使用MATLAB解决以下Lorenz初始值问题
我编写了一个函数,该函数将三个微分方程组作为输入,并使用 带有步长的Runge-Kutta方法求解该系统。
我使用MATLAB生成了解决方法的GIF。
可下载资源
我使用MATLAB解决以下Lorenz初始值问题:

1961年冬天,年轻的麻省理工学院气象学助教洛伦兹(1917-2008),在一台Royal McBee LPG-30计算机上,用一个仅包含12个微分方程的简单模式进行气候模拟。在完成了一次计算后,他想用同样的模式重复。为了节省时间,他没有从头到尾重复这次计算,而是从程序的中段开始。于是他把上一次计算到这个位置输出的数据,作为这次计算的初始条件。然后,为了避开计算机恼人的噪音,他出去喝了杯咖啡。回来的时候,他被惊呆了。根据常识,同样的程序和数据显然会导致同样的结果。但是第二次的预报结果与上一次大不一样。开始他认为是计算机的故障,排除了这种可能后,他发现,他输入的不是完整的数据。他当时用的计算机,储存数据的容量是小数点后六位数字,但是在打印输出数据时,为了节省纸张,只输出小数点后三位数字。而洛伦兹在给第二次计算输入初始条件的时候,只输入了小数点后的三位,与精确的数据有不到0.1%的误差。就是这个原本应该忽略不计的误差,使最终的结果大相径庭。这让洛伦兹意识到,完美的长期天气预报是不可能的。一个完美的预报不仅需要完美的气候模式,而且需要对温度、湿度、风和所有其他气象条件的精确测量,任何微小的误差,将导致完全不一样的气候现象。
1963年,洛伦兹在美国《气象学报》上发表了题为“确定性的非周期流”的论文,提出了在确定性系统中的非周期现象。第二年,他发表了另外一篇论文,指出对于模式中参数的微小改变将导致完全不一样的结果,使有规律的、周期性的行为,变成完全混乱的状态。不过,他的发现没有引起任何注意,直到十年后他提出“蝴蝶效应”这个通俗却惊人的想法,才让人们了解到这一现象的重要性。
1972年美国科学发展学会第139次会议上,洛伦兹发表了题为“可预测性:巴西一只蝴蝶扇动翅膀,能否在得克萨斯州掀起一场龙卷风”的演讲。他认为,一个微小的初始条件变化可能导致一连串逐渐放大的改变,最终导致完全不同的结果——这个看似荒谬的论断,打碎了所有人关于“因果决定论可预测度”所存的幻想,最终产生了当今世界最伟大的理论之一——“混沌理论”。洛伦兹后来说,他原本想用海鸥做比喻的。一个同事告诉他,用“蝴蝶”可能会更生动,而选择“巴西”则纯粹是为了押韵。
1987年,《纽约时报》科技部主任詹姆斯格莱克(James Gleick)在采访了200多名科学家后,撰写了一本后来享誉世界的畅销书《混沌:开创新科学》。第一章的标题就是“蝴蝶效应”,介绍了洛伦兹第一次发现混沌现象的过程,不过他给蝴蝶搬了个家——“今天北京一只蝴蝶拍翅对空气造成扰动,可能触发下个月纽约的暴风雨。”这本书后来被翻译成19种文字,也在上世纪90年代初给中国读者带来了“混沌”的概念。
这种最初只在气象预报中出现的现象,后来被发现存在于众多的自然和社会系统中,诸如人口的涨落、精神病的发病、心率的节奏、雪花的形状、股市的波动、汇率的变化等,都存在混沌现象。在洛伦兹之后,在计算机的帮助下,人类开始用“混沌理论”研究自然界和社会中的不规则、不连续和不稳定的方面,开启了简化复杂现象的可能性。
我编写了一个函数,该函数将三个微分方程组作为输入,并使用 带有步长的Runge-Kutta方法求解该系统。
我使用MATLAB生成了解决方案的GIF。

% 输入:
% f1,f2,f3 = y'(t,y) as a string
% y0 = initial condition
% inter = interval
% h = step size
% 调用函数求解Lorenz方程
L=LorenzRK('-10*y1+10*y2','-y1*y3+28*y1-y2','y1*y2-(8/3)*y3',[0,50],[5,5,5],.01)
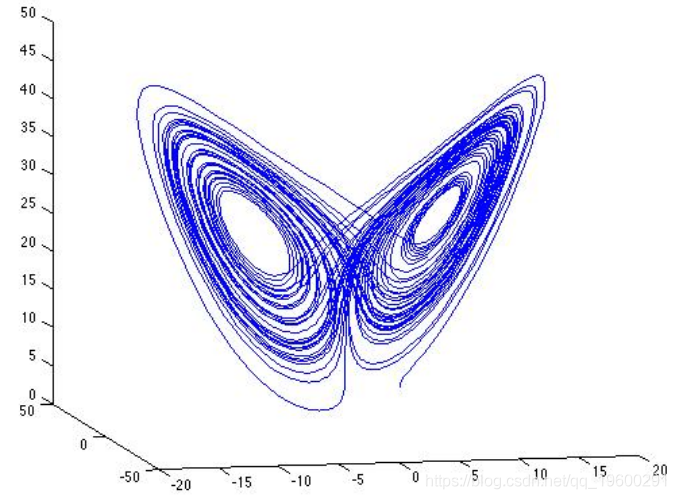
% 绘制Lorenz解
plot3(L(:,2),L(:,3),L(:,4))
% 创建GIF:
L=LorenzRK('-10*y1+10*y2','-y1*y3+28*y1-y2','y1*y2-(8/3)*y3',[0,50],[5,5,5],.01)

 2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载
2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载 2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载
2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载 Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究
Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化



