
主题建模是一种在大量文档中查找抽象主题的艺术方法。
作为无监督的机器学习方法,主题模型不容易评估,因为没有标记的“基础事实”数据可供比较。
可下载资源
然而,由于主题建模通常需要预先定义一些参数(首先是要发现的主题ķ的数量),因此模型评估对于找到给定数据的“最佳”参数集是至关重要的。
1 文本生成
1.1 文本生成过程
对于一篇文档,可以看成是一组有序的词的序列。从统计学的角度看,文档的生成可以看成是上帝抛掷骰子生成的结果,每一次抛掷骰子都生成一个单词,抛掷
次生成一篇文档。对于该抛掷的过程,存在两个不同学派的观点:
-
频率学派认为,上帝只有一个骰子,这个骰子有V面,每个面对应一个单词。上帝生成文档是通过独立抛掷
次产生n个词;
-
贝叶斯学派认为,上帝有一个装有多个骰子的坛子,每个骰子有V面,每个面对应一个单词(不同骰子每个面概率不同)。上帝生成文档是通过先在坛子里拿一个骰子,然后再独立抛掷
次产生
个词。
LDA(Latent Dirichlet Allocation)是Blei等人基于上述贝叶斯学派的观点提出的一种生成文档的方法,该方法假设每个单词是由背后的一个潜在隐藏的主题中抽取出来。对于语料库中的每篇文档,其生成过程为:(1)选择主题;(2)生成单词;(3)组成文档。具体过程如下:
-
对于每篇文档,其主题存在一个分布,根据该主题分布抽取一个主题;
-
对于每个主题,其单词存在一个分布,根据该分布抽取一个单词;
-
重复过程2直到遍历文档中的每一个词。
那么上述主题分布和单词分布都是什么分布呢?且分布需要满足什么性质呢?
1.2 贝叶斯规则
对于一篇文档,构成文档的单词是可观测的,但文档的主题是不可观测的,因此我们需要根据可观测的单词去估计隐藏的主题分布。根据贝叶斯规则:
其中:
-
表示根据观测的数据,得出主题的后验分布;
-
表示主题的先验分布;
-
表示观测数据的似然函数;
上述就是贝叶斯思想:对于一个未知的分布,先假设其服从先验分布(来源于以前做试验数据计算得到,或来自于人们的主观经验),通过观测到的数据,根据贝叶斯规则计算对应的后验分布。很显然时刻的后验分布为
次的先验分布,因此需要满足先验分布和后验分布具有相同的形式,即上述中
与
具有相同的分布形式。
2 前置知识
2.1 gamma函数
根据阶乘可知:,但是当出现小数时,比如计算
则阶乘无法直接计算,因此才出现了阶乘的函数形式——gamma函数:
,因此有
2.2 二项分布
对于次独立试验,假设每次试验的结果只有两种:成功与失败。成功的概率为
,则失败的概率为
。
次独立实验的结果中,成功的次数为
,失败的次数为
,则定义似然函数为:
似然函数表示观测数据出现的概率,上式满足:
2.3 beta分布
其中为beta分布的超参数,表示伪计数。
参数解释:假设NBA运动员的投篮命中率服从beta分布,对一个刚进联盟的篮球运动员的命中率进行建模,很明显该运动员的命中率也服从beta分布。此时利用上赛季全联盟所有人的投篮命中数,打铁数
,作为该运动员命中率beta分布的参数。且以
作为该运动员的先验命中率。此后,根据该运动员投篮数据的增加,去更新其投篮命中率的计算。
期望计算:
对于分布,有
则有
代入上式得
2.4 共轭先验分布
上述二项式分布的似然函数为
先验的beta分布为
根据贝叶斯规则可得后验分布
即后验分布仍满足beta分布,与先验一致。
先验分布
后验分布
其中为伪计数,
为观测的数据。
综上,二项分布对应的共轭先验为beta分布,其意思为,beta分布*二项分布的结果仍未beta分布。
3 Dirichlet分布
3.1 多项式分布
对二项式分布推广到k种结果的情况,此时变为多项式分布,对应的似然函数为
其中,,
3.2 Dirichlet分布
对beta分布推广到k种结果的情况,此时表为Dirichle分布
其中
同2.3,Dirichlet分布的期望为:。
3.3 多项式分布与Dirichlet分布共轭
同2.4可得
先验分布
后验分布
其中为伪计数,
为观测的数据。
4 LDA模型
4.1 模型表示
现在问题是这样的,我们有篇文档,对应第
个文档有
个单词。我们的目标是找到每一篇文档的主题分布和每一个主题单词的分布。在LDA模型中,我们需要先假定一个主题数目
,这样所有的分布就都基于
个主题展开。
对于语料库中的每篇文档,LDA定义了一个生成过程,以1文本生成部分的投骰子为例,如下:
-
。这个过程表示在生成第
篇文档的时候,在D个服从
的坛子中找到骰子
,然后投掷这枚骰子生成第n个词的主题(topic)编号
;
-
。这个过程表示在生成第
篇文档第
个词的时候,在K个服从
的坛子找到主题编号为
的骰子,然后投掷这枚骰子生成单词
简单来说,步骤1就是,步骤2就是
,根据条件概率的基本公式可得:
而LDA的目标就是要找出每个词后潜在的主题,所以为了达到这个目标,需要计算后验概率:
4.2 直接计算
针对上述后验概率的计算,在这里对其计算复杂度进行分析。
按照离散分布边缘概率的处理方式,文档中一个单词的全概率为
因此对于上述后验概率计算中的分母,其表示为所有单词的联合概率,则有
每个单词都对应着个主题,总共有
个单词,因此分母计算陷入了
项难题,这个离散状态空间太大以至于无法枚举。
5 模型求解
在上节结尾可知,现实中,往往很难求出精确的概率,因此常常采用近似推断的方法。近似推断的方法大致可分为两大类:第一类是使用随机化采样完成近似,比如Gibbs采样;第二类是使用确定性近似完成近似推断,比如变分推断。
概率LDA主题模型的评估方法
使用未标记的数据时,模型评估很难。这里描述的指标都试图用理论方法评估模型的质量,以便找到“最佳”模型。
评估后部分布的密度或发散度
有些指标仅用于评估后验分布(主题 – 单词和文档 – 主题分布),而无需以某种方式将模型与观察到的数据进行比较。
使用美联社数据查找最佳主题模型
计算和评估主题模型
主题建模的主要功能位于tmtoolkit.lda_utils。
import matplotlib.pyplot as plt # 绘制结果
plt.style.use('ggplot')
# 读取数据
from tmtoolkit.utils import unpickle_file
# 模型评估
from tmtoolkit.lda_utils import tm_lda
# 建立模型评估图
from tmtoolkit.lda_utils.common import results_by_parameter
from tmtoolkit.lda_utils.visualize import plot_eval_results接下来,我们加载由文档标签,词汇表(唯一单词)列表和文档 – 术语 – 矩阵组成的数据dtm。我们确保dtm维度合适:
doc_labels, vocab, dtm = unpickle_file('ap.pickle')
print('%d documents, %d vocab size, %d tokens' % (len(doc_labels), len(vocab), dtm.sum()))
assert len(doc_labels) == dtm.shape[0]
assert len(vocab) == dtm.shape[1]现在我们定义应该评估的参数集我们设置了一个常量参数字典。const_params,它将包含不变参数用于计算每个主题模型。我们还设置了varying_params,包含具有不同参数值的字典的不同参数列表:
在这里,我们想要从一系列主题中计算不同的主题模型ks = [10, 20, .. 100, 120, .. 300, 350, .. 500, 600, 700]。由于我们有26个不同的值ks,我们将创建和比较26个主题模型。请注意,还我们alpha为每个模型定义了一个参数1/k(有关LDA中的α和测试超参数的讨论,请参见下文)。参数名称必须与所使用的相应主题建模包的参数匹配。在这里,我们将使用lda,因此我们通过参数,如n_iter或n_topics(而与其他包的参数名称也会有所不同num_topics,不是而n_topics)。
我们现在可以使用模块中的evaluate_topic_models函数开始评估我们的模型tm_lda,并将不同参数列表和带有常量参数的字典传递给它:
默认情况下,这将使用所有CPU内核来计算模型来并行评估它们。
该plot_eval_results函数使用在评估期间计算的所有度量创建³³绘图。之后,如果需要,我们可以使用matplotlib方法调整绘图(例如添加绘图标题),最后我们显示和/或保存绘图。
结果
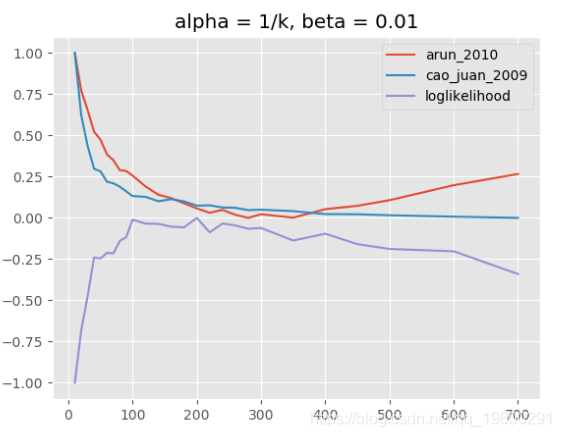
主题模型评估,alpha = 1 / k,beta = 0.01
请注意,对于“loglikelihood”度量,仅报告最终模型的对数似然估计,这与Griffiths和Steyvers使用的调和均值方法不同。无法使用Griffiths和Steyvers方法,因为它需要一个特殊的Python包(gmpy2) ,这在我运行评估的CPU集群机器上是不可用的。但是,“对数似然”将报告非常相似的结果。
阿尔法和贝塔参数
除了主题数量之外,还有alpha和beta(有时是文献中的eta)参数。两者都用于定义Dirichlet先验分布,用于计算各自的后验分布。Alpha是针对特定于文档的主题分布的先验的“参数”,β是针对主题特定的单词分布的先验的参数 。
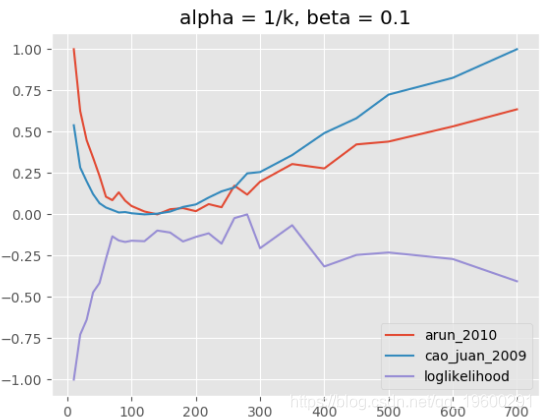
主题模型,alpha = 1 / k,beta = 0.1
当我们使用与上述相同的alpha参数和相同的k范围运行评估时,但是当β= 0.1而不是β= 0.01时,我们看到对数似然在k的较低范围内最大化,即大约70到300(见上图) 。
组合这些参数有很多种可能性,但是解释这些参数通常并不容易。
下图显示了不同情景的评估结果:(1)α固定,β的值取决于k,(2)α和β都固定, (3)α和β均取决于k。
随时关注您喜欢的主题
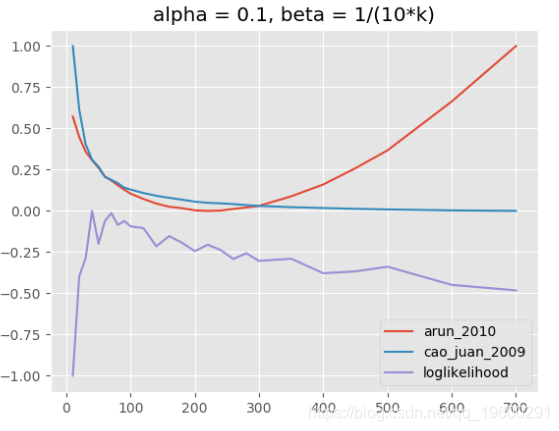
(1)主题模型,alpha = 0.1,beta = 1 /(10k)
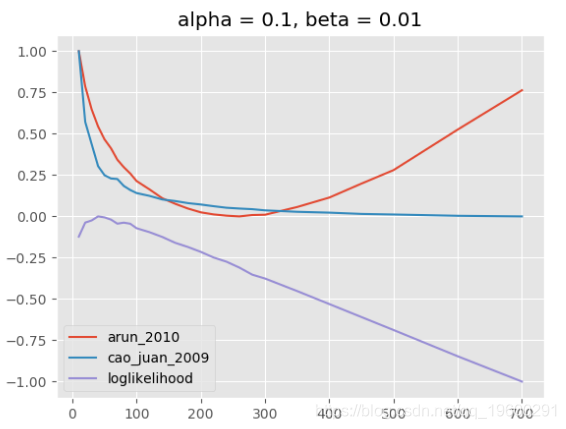
(2)主题模型,alpha = 0.1,beta = 0.01
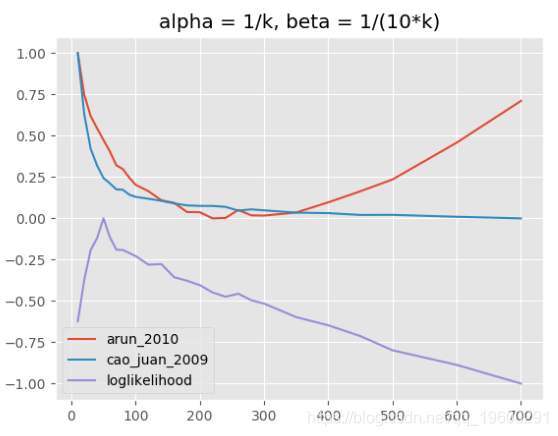
(3)主题模型,alpha = 1 / k,beta = 1 /(10k)
LDA超参数α,β和主题数量都相互关联,相互作用非常复杂。在大多数情况下,用于定义模型“稀疏性”的beta的固定值似乎是合理的,这也是Griffiths和Steyvers所推荐的。一个更精细的模型评估,具有不同的alpha参数(取决于k)使用解释的指标可以完成很多主题。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程
Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程 Python用SentenceTransformer、OLS、集成学习、模型蒸馏情感分类金融新闻文本|附代码数据
Python用SentenceTransformer、OLS、集成学习、模型蒸馏情感分类金融新闻文本|附代码数据 Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据
Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据



