POT模型其主要动机是为高洪水流量的概率模型提供实用工具。但是,EVT的优势在于结果不取决于要建模的过程。因此,人们可以使用POT来分析降水,洪水,金融时间序列,地震等。
最近我们被客户要求撰写关于POT的研究报告,包括一些图形和统计输出。POT模型其主要动机是为高洪水流量的概率模型提供实用工具。但是,EVT的优势在于结果不取决于要建模的过程。因此,人们可以使用POT来分析降水,洪水,金融时间序列,地震等。
可下载资源
特征
POT软件包可以执行单变量和双变量极值分析;一阶马尔可夫链也可以考虑。例如,目前使用18个 估算器拟合(单变量)GPD 。这些估算器依靠三种不同的技术:
- 极大似然:MLE,LME,MPLE
- 动量法:MOM,PWM,MED
- 距离最小化:MDPD和MGF估计器。
估计VaR有两类主要的方法,非参数(Nonparametric)方法和参数(parametric)方法。非参数方法基于历史收益率数据或者模拟收益率数据的分布,来获得对VaR的估计。参数方法则通过对于收益率随机变量的分布类型和参数做出估计,通过分布函数(概率密度函数)来对VaR做出估计。非参数方法由于样本数据的随机性以及尾部数据的稀少性,从而对于极端损失的估计不够精确。参数方法中的分布函数是对于全部收益率数据的一种数学概括,往往这种概括并不能很好地描述尾部的情况。作为对上述两类方法的结合,极值理论(Extreme Value Theory)以尾部(亏损)区域的收益率数据为基础,先估计出尾部数据的分布函数(概率密度函数),再利用分布函数对VaR做出估计。由于分布函数是基于尾部数据得到的,所以对于VaR的预测也更加地准确。
例如,收集从1960年到1987年10月16日期间的S&P 500指数的日收益率数据,然后找出每一年的最大的日亏损率数据,一共有28个数据点(极端亏损数据),其中最大的单日跌幅为6.7%。以Frechet分布来拟合28个亏损数据点,得到具体的分布函数。然后根据所得到的分布函数,可以求出置信水平为98%的VaR为24%,也就是说预计每50年里有1年会出现单日跌幅超过24%的情况,根据分布函数所预测的极端损失(24%)远远高于经验数据所反映的极端损失(6.7%)。在休市两天以后,1987年10月19日,美国股市崩溃,S&P 500指数单日跌幅超过20%。从中可以看到,极值理论对于尾部损失预测的可靠性较高。
极端亏损数据的采集方式有两种,一种称为Peaks over Threshold (POT)方法,另一种称为Block Maxima (BM)方法。POT方法选定一个门槛亏损率,然后将收益率经验数据中所有亏损幅度超过门槛收益率的数据保留下来,作为拟合尾部分布的数据基础。
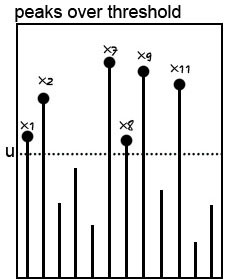
BM方法将所有的收益率数据根据时间顺序排列,并根据固定的间距分成许多组,然后从每一组中选出最大值(亏损为正数,收益为负数),将选出的数据点作为拟合尾部分布的数据基础。
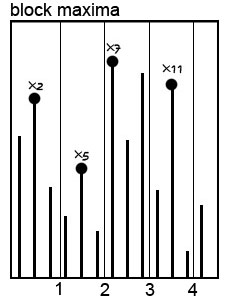
极端数据的采集方式不同,在此基础上拟合的分布类型也不同。POT方法采集的数据,用Generalized Pareto分布进行拟合; BM方法采集的数据,用Generalized Extreme Value分布来拟合。在分布参数的选择时,需要考虑到损失数据的肥尾现象。
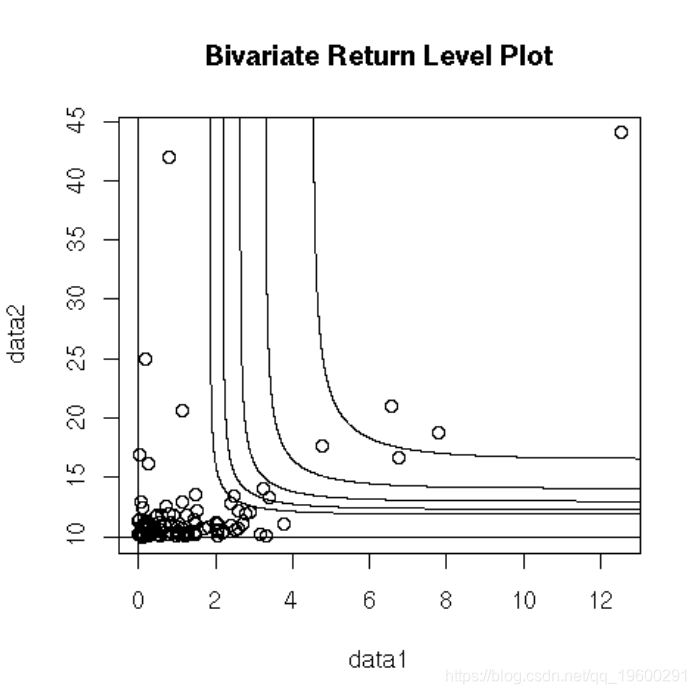
与单变量情况相反,没有用于对超过阈值的双变量超出进行建模的有限参数化。POT允许对双变量GPD进行6种参数化:对数模型,负对数模型和混合模型-以及它们各自的不对称版本。
最后,可以使用二元GPD拟合一阶马尔可夫链,以实现两个连续观测值的联合分布。
在本节中,我们明确介绍了软件包中一些最有用的功能。 但是,对于完整的描述,用户可能希望查看软件包的小插图和软件包的html帮助。
GPD 计算:
模拟来自GPD(0,1,0.2)的样本:
x <- rgpd(100, 0, 1, 0.2)
##评估x = 3时的密度和不超过的概率:
dgpd(3, 0, 1, 0.2); pgpd(3, 0, 1, 0.2)
#计算非超出概率为0.95的分位数:
qgpd(0.95, 0, 1, 0.2)
y <- rbvgpd(100, mo
##评估不超过(5,14)的可能性
pbvgpd(c(3,15), mode
GPD 拟合
##最大似然估计(阈值= 0):
mle <- fgpd(x, 0)
##最大似然估计(阈值= 0):
pwu <- fgpd(x, 0, "pwmu")
##最大拟合优度估算器:
adr <- fgpd(x, 0, "mgf"
##指定已知参数:
fgpd(x, 0, "mple",
##指定数值优化的起始值:
fgpd(x, 0, "mdpd", start =
##拟合具有逻辑依存关系的双变量GPD:
log <- fitbv绘图用于单变量和双变量情况的通用函数:
plot(mle); plot(log) 
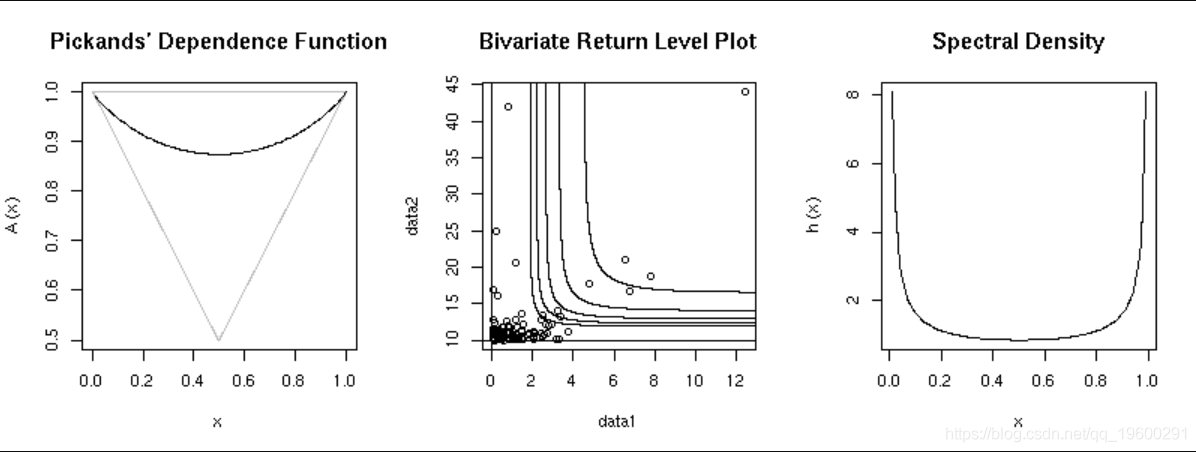
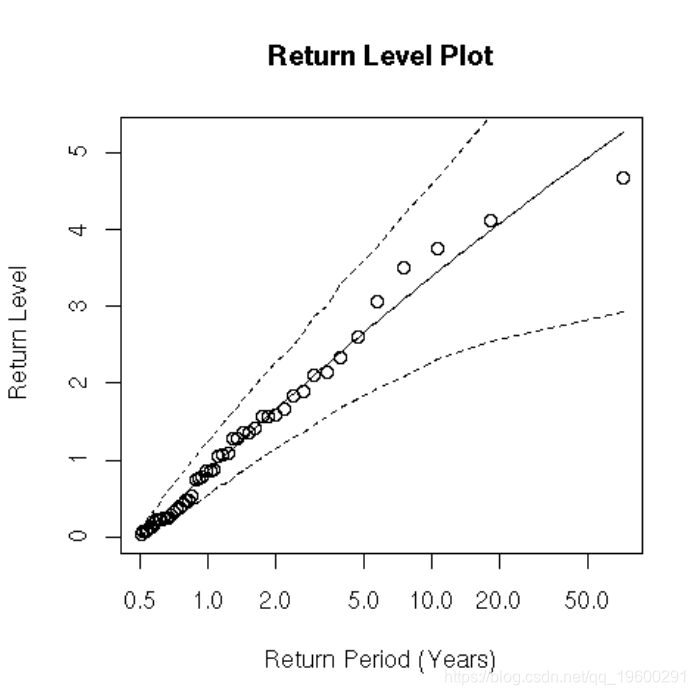
返回等级图:
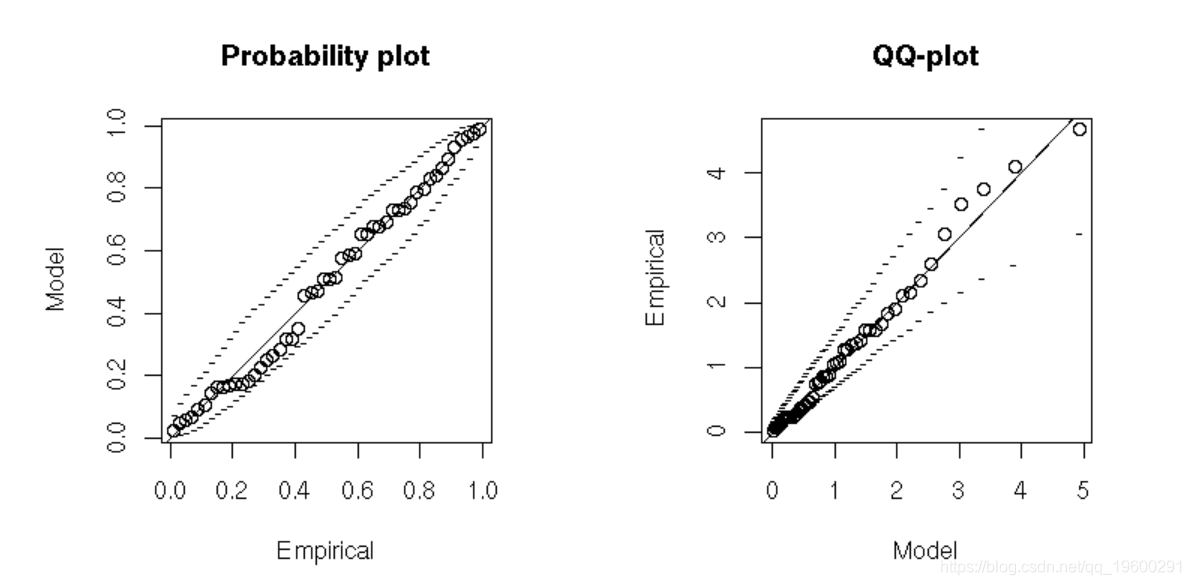
绘制密度
随时关注您喜欢的主题
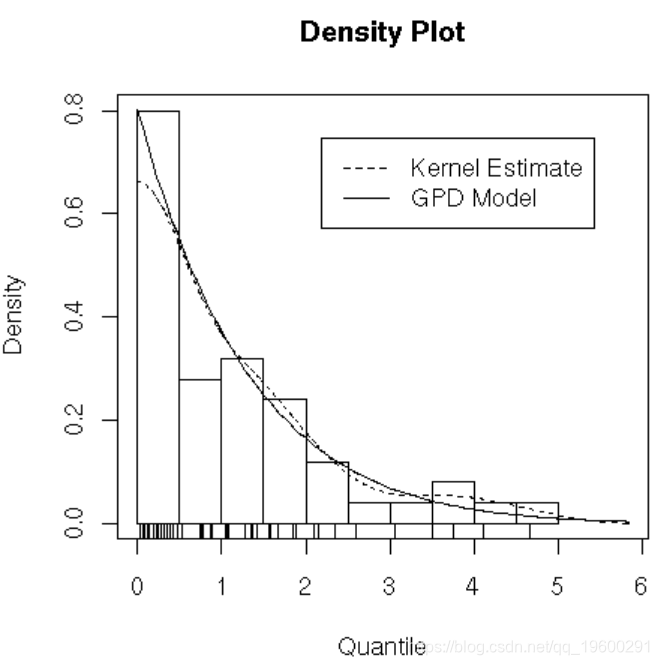
绘制Pickands的依赖函数:
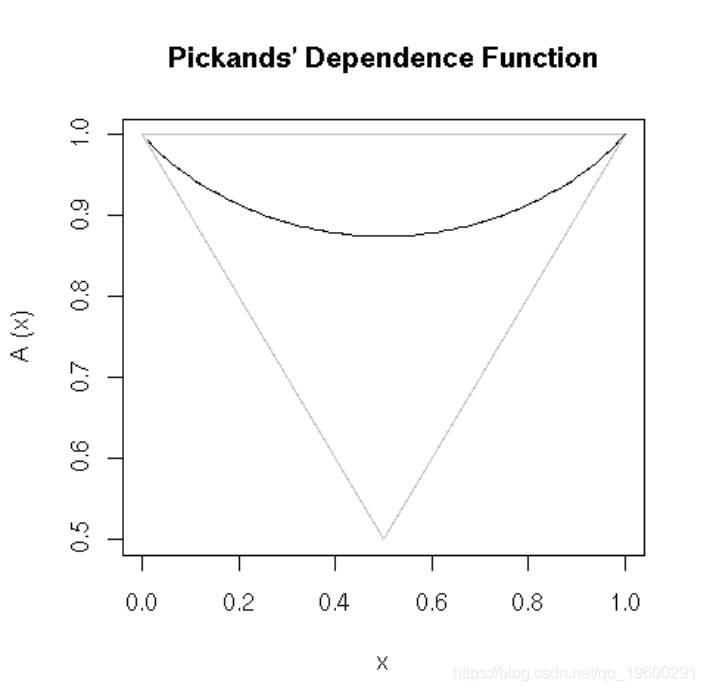
光谱密度图
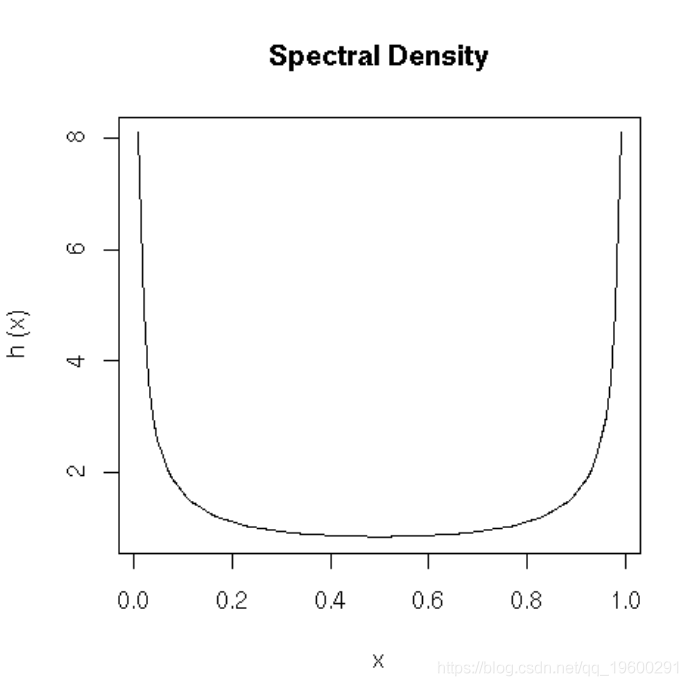
对数似然(分位数)
confint(mle, prob = 0.95)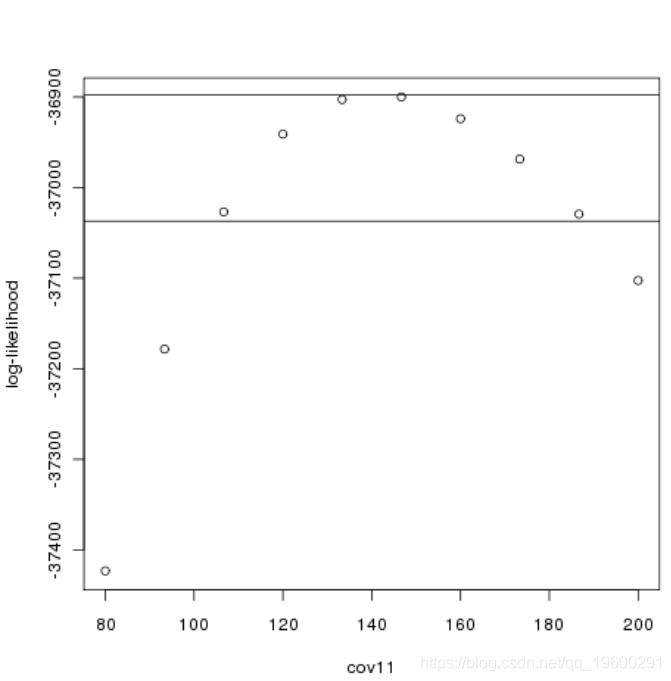
##对数似然(参数):
confint(mle, "shape") 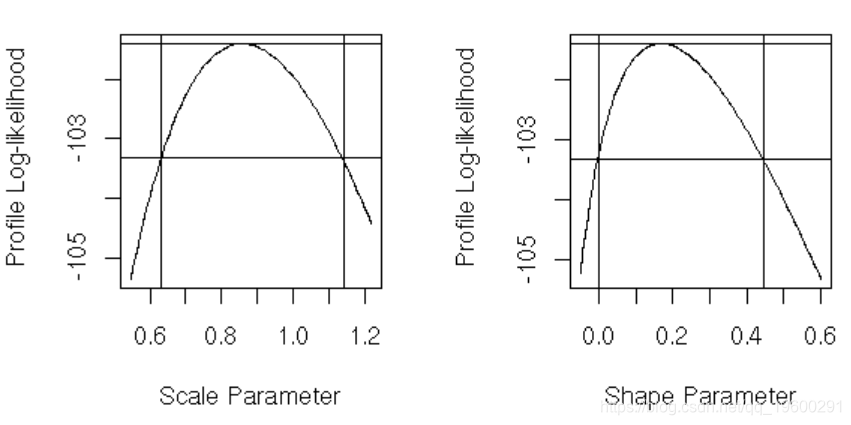
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标
【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标 R语言宏观经济学:IS-LM曲线可视化货币市场均衡
R语言宏观经济学:IS-LM曲线可视化货币市场均衡
