在引入copula时，大家普遍认为copula很有趣，因为它们允许分别对边缘分布和相依结构进行建模。
最近我们被客户要求撰写关于copula的研究报告，包括一些图形和统计输出。给定一些边缘分布函数和一个copula，那么我们可以生成一个多元分布函数，其中的边缘是前面指定的。
考虑一个二元对数正态分布
> library(mnormt)
> set.seed(1)
> Z=exp(rmnorm(25,MU,SIGMA))我们可以从边缘分布开始。
当边缘分布（marginal probability distribution）不同的随机变量（random variable），互相之间并不独立的时候，此时对于联合分布的建模会变得十分困难。此时，在已知多个已知边缘分布的随机变量下，Copula函数则是一个非常好的工具来对其相关性进行建模。
什么是Copula函数？
copula这个单词来自于拉丁语，意思是“连接”。最早是由Sklar在1959年提出的，即Sklar定理：
以二元为例，若 是一个具有连续边缘分布的
与
的二元联合分布函数，那么存在唯一的Copula函数
，使得
。反之，如果
是一个copula函数，而
和
是两个任意的概率分布函数，那么由上式定义的
函数一定是一个联合分布函数，且对应的边缘分布刚好就是
和
。
Sklars theorem : Any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the two variable.
Sklar认为，对于N个随机变量的联合分布，可以将其分解为这N个变量各自的边缘分布和一个Copula函数，从而将变量的随机性和耦合性分离开来。其中，随机变量各自的随机性由边缘分布进行描述，随机变量之间的耦合特性由Copula函数进行描述。换句话说，一个联合分布关于相关性的性质，完全由其Copula函数决定。
如果已知 ，
和
，则Copula函数可以表达为：
这里 代表
的反函数，或者叫CDF的逆变换、逆累积分布函数。
Copula理论的数学表达
假设 是
个随机变量，它们各自的边缘分布分别为
，它们的联合分布为
，则存在一个将边缘分布和联合分布“连接”起来的函数
，使得：
而根据边缘分布的CDF的逆变换，即 ，则可以得到Copula函数的表达形式：
补充知识：概率积分变换（Probability Integral transform）
在概率论中，概率积分变换(也称为均匀的普适性)是指将任意给定连续分布的随机变量的数据值转换成具有标准均匀分布的随机变量的结果。
简单解释一下概率积分变换[1]：如果 和
都是随机变量（Random Variables，RV），而
、
分别是二者的累计概率分布函数，即
那么： 和
都服从均匀分布，
简要的数学证明如下：
换句话说，任何边际分布的CDF值都均匀分布在区间[0,1]上。如果从任意分布中随机抽取，那么抽取该分布的最大值(U=1)的概率与抽取可能的最小值(U=0)或中值(U= 5)的概率相同。而copula实际上是它所建模的随机变量的CDFs的联合分布。
meanlog sdlog
1.168 0.930
(0.186 ) (0.131 )
meanlog sdlog
2.218 1.168
(0.233 ) (0.165 )基于这些边缘分布，并考虑从该伪随机样本获得的copula参数的最大似然估计值，从数值上讲，我们得到
> library(copula)
> Copula() estimation based on 'maximum likelihood'
and a sample of size 25.
Estimate Std. Error z value Pr(>|z|)
rho.1 0.86530 0.03799 22.77但是，由于相依关系是边缘分布的函数，因此我们没有对相依关系进行单独处理。如果考虑全局优化问题，则结果会有所不同。可以得出密度
> optim(par=c(0,0,1,1,0),fn=LogLik)$par
[1] 1.165 2.215 0.923 1.161 0.864 差别不大，但估计量并不相同。从统计的角度来看，我们几乎无法分别处理边缘和相依结构。我们应该记住的另一点是，边际分布可能会错误指定。例如，如果我们假设指数分布，
fitdistr(Z[,1],"exponential")
rate
0.222
(0.044 )
fitdistr(Z[,2],"exponential"
rate
0.065
(0.013 )高斯copula的参数估计
Copula() estimation based on 'maximum likelihood'
and a sample of size 25.
Estimate Std. Error z value Pr(>|z|)
rho.1 0.87421 0.03617 24.17 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The maximized loglikelihood is 15.4
Optimization converged由于我们错误地指定了边缘分布，因此我们无法获得统一的边缘。如果我们使用上述代码生成大小为500的样本，
barplot(counts, axes=FALSE,col="light blue"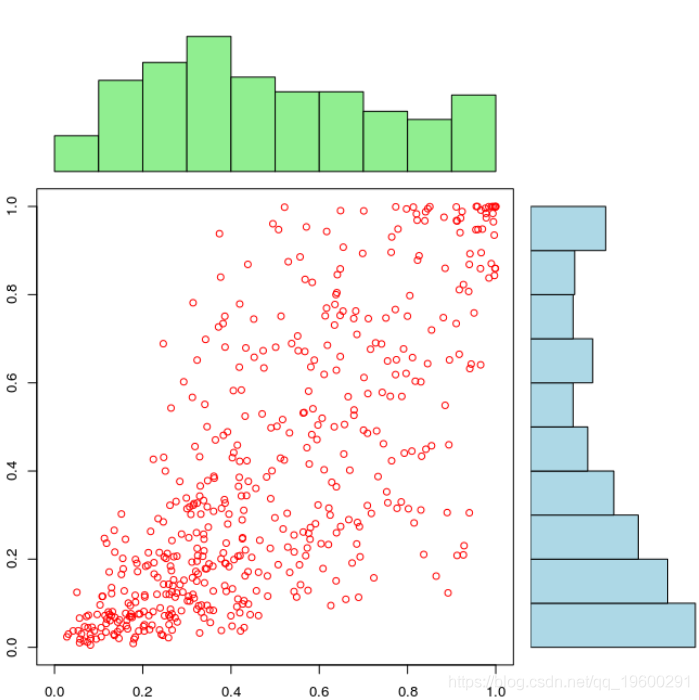
如果边缘分布被很好地设定时，我们可以清楚地看到相依结构依赖于边缘分布，
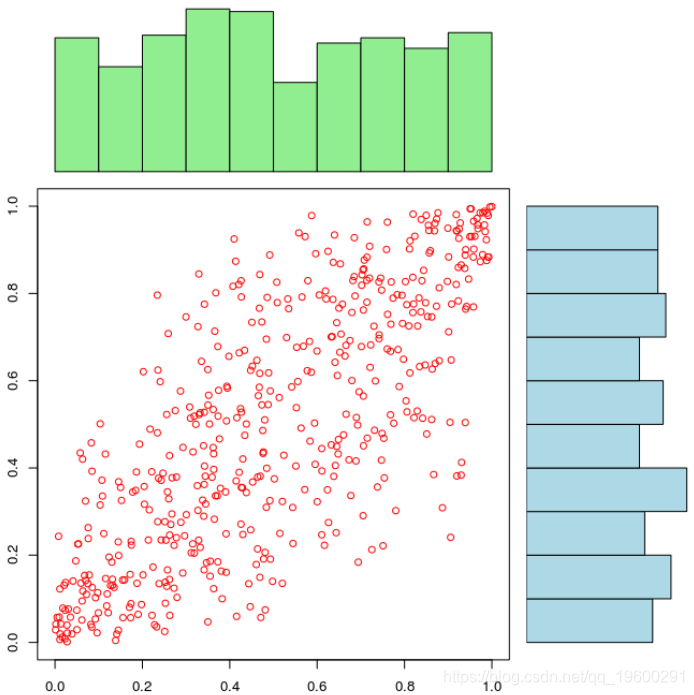
copula模拟股市中相关随机游走
接下来我们用copula函数模拟股市中的相关随机游走
#*****************************************************************
# 载入历史数据
#******************************************************************
load.packages('quantmod')
data$YHOO = getSymbol.intraday.google('YHOO', 'NASDAQ', 60, '15d')
data$FB = getSymbol.intraday.google('FB', 'NASDAQ', 60, '15d')
bt.prep(data, align='remove.na')
#*****************************************************************
# 生成模拟
#******************************************************************
rets = diff(log(prices))
# 绘制价格
matplot(exp(apply(rets,2,cumsum)), type='l')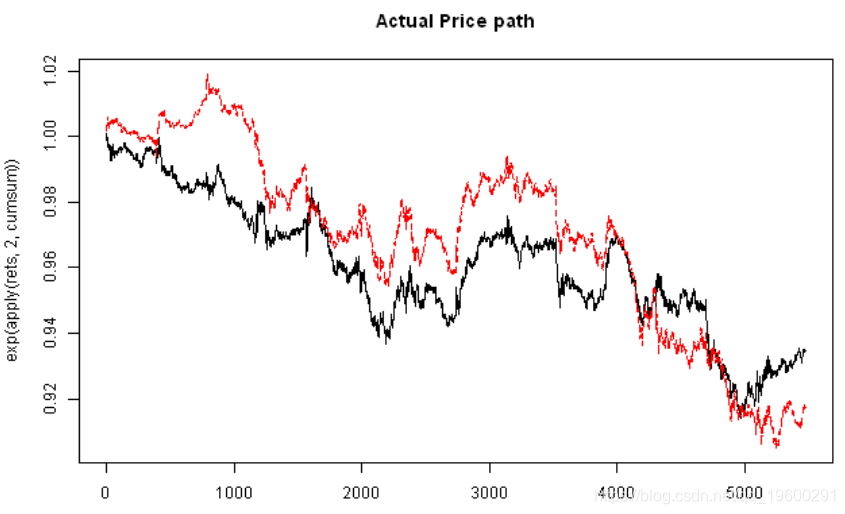
# 可视化分布的辅助函数
# 检查Copula拟合的Helper函数
# 模拟图与实际图
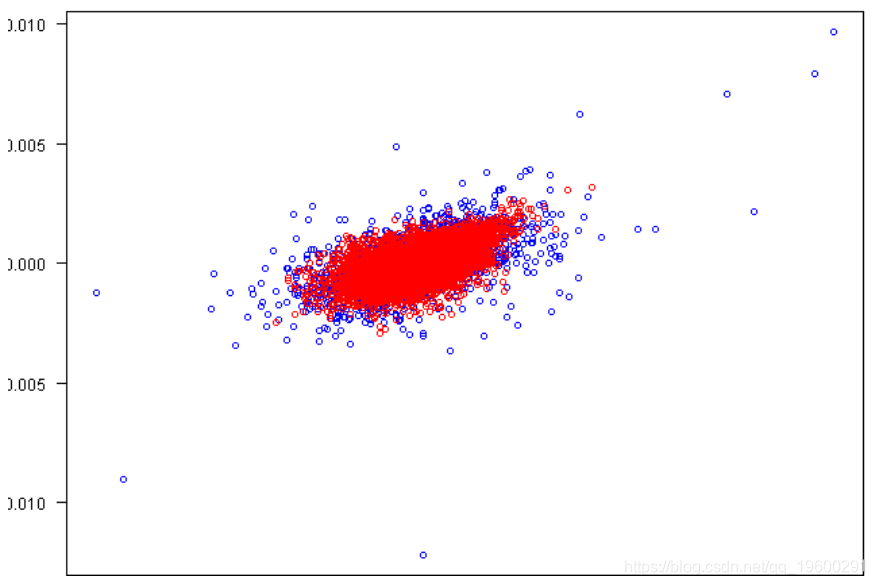
plot(rets[,1], rets[,2], xlab=labs[1], ylab=labs[2], col='blue', las=1)
points(fit.sim[,1], fit.sim[,2], col='red')
# 比较模拟和实际的统计数据
temp = matrix(0,nr=5,nc=2)
print(round(100*temp,2))
# 检查收益率是否来自相同的分布
for (i in 1:2) {
print(labs[i])
print(ks.test(rets[,i], fit.sim[i]))
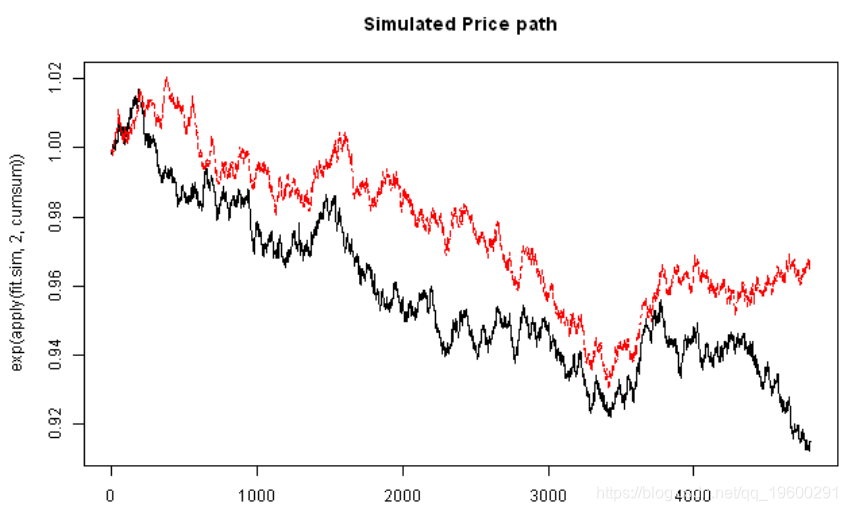
# 绘制模拟价格路径
matplot(exp(apply(fit.sim,2,cumsum)), type='l', main='Simulated Price path')
# 拟合Copula
load.packages('copula')随时关注您喜欢的主题
# 通过组合拟合边缘和拟合copula创建自定义分布
margins=c("norm","norm")
apply(rets,2,function(x) list(mean=mean(x), sd=sd(x)))
# 从拟合分布模拟
rMvdc(4800, fit)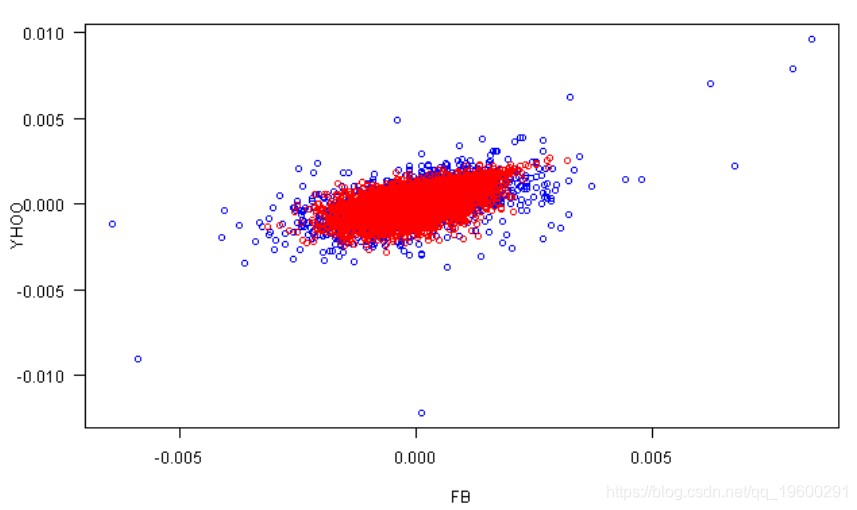
Actual Simulated
Correlation 57.13 57.38
Mean FB -0.31 -0.47
Mean YHOO -0.40 -0.17
StDev FB 1.24 1.25
StDev YHOO 1.23 1.23FB
Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.9404, p-value = 0.3395
alternative hypothesis: two-sided
HO
Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.8792, p-value = 0.4222
alternative hypothesis: two-sided
visualize.rets(fit.sim)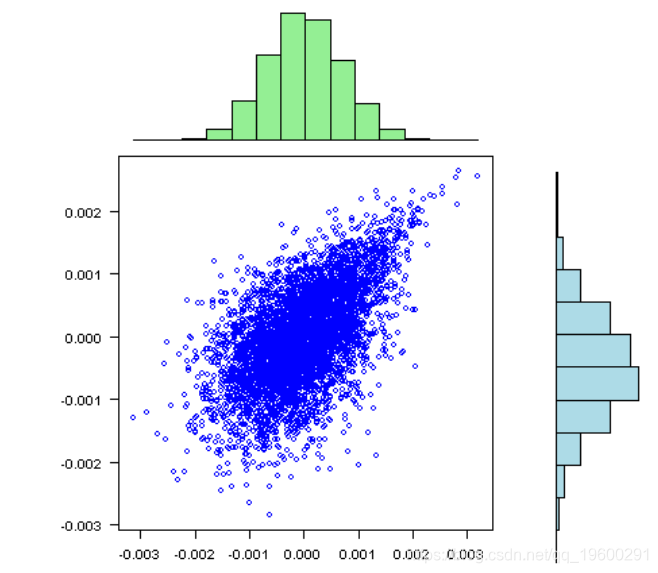
# qnorm(runif(10^8)) 和 rnorm(10^8) 是等价的
uniform.sim = rCopula(4800, gumbelCopula([email protected], dim=n))
Actual Simulated
Correlation 57.13 57.14
Mean FB -0.31 -0.22
Mean YHOO -0.40 -0.56
StDev FB 1.24 1.24
StDev YHOO 1.23 1.21FB
Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.7791, p-value = 0.5787
alternative hypothesis: two-sided
HO
Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.795, p-value = 0.5525
alternative hypothesis: two-sided
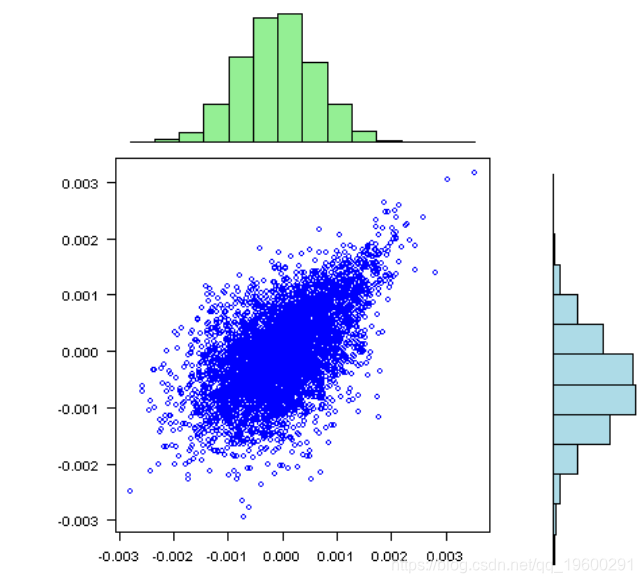
vis(rets)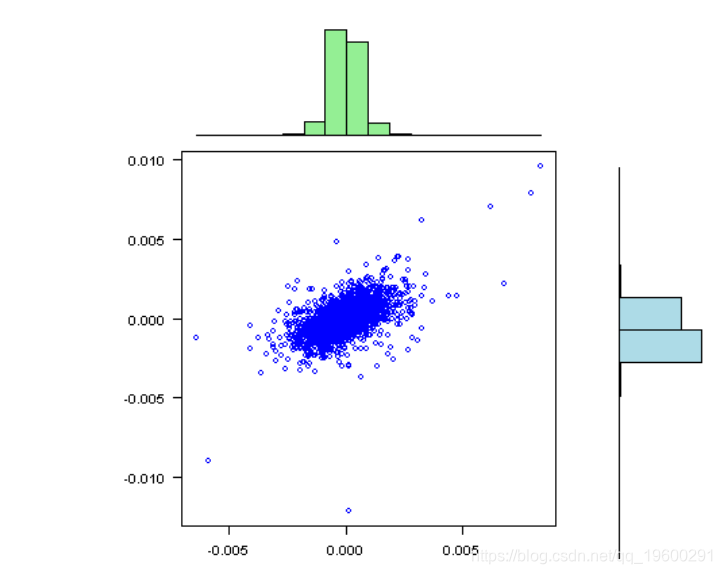
标准偏差相对于均值而言非常大，接近于零；因此，在某些情况下，我们很有可能获得不稳定的结果。
R语言代做编程辅导和解答GLM Coursework
MATLAB用GARCH-EVT-Copula模型VaR预测分析股票投资组合
R语言分析上海空气质量数据：kmean聚类、层次聚类、时间序列分析：arima模型、指数平滑法
R语言收益率和波动性模拟股票价格COMP226带自测题
