我将建立道琼斯工业平均指数（DJIA）日交易量对数比的ARMA-GARCH模型。
获取数据
可下载资源
load(file='DowEnvironment.RData') 金融资产的波动是一个非常重要的概念，它与资产的风险直接相关，因此对资产的波动模式进行建模是量化投资中的一个重要课题。一般来讲，波动建模有以下量化投资方向的应用：
-
期权定价：波动率是影响期权价值的重要因素；
-
风险度量和管理：在VaR的计算中波动率是主要影响因素，根据波动率决定交易策略的杠杆；
-
资产价格预测和模拟：通过Garch簇模型对资产价格的时间序列进行预测和模拟；
-
调仓：盯住波动率的调仓策略，如一个tracing指数的策略；
-
作为交易标的：在VIX、ETF以及远期中波动率作为标的可以直接交易。
在讲Garch模型之前，我们必须对同方差和异方差的概念进行回顾。在时间序列的弱平稳条件中二阶矩是一个不变的、与时间无关的常数。在理想条件下，如果这个假设是成立的，那么金融时间序列的预测将会变得非常简单，采用ARIMA等线性模型就能做不错的预测。然而采用Ariam等模型对金融事件序列建模效果是非常差的，原因就在于金融事件序列的异方差性。这种非平稳性无法用简单的差分去消除，其根本原因在于其二阶矩随时间t变化而变化。
异方差描述的是金融时间序列大的趋势，时间跨度相对较长。金融时间序列的另一个特征是波动聚集，它是在小时间尺度下的波动特性（可以理解为小尺度下的异方差表现）。一般来讲，金融时间序列的波动具有大波动接着大波动，小波动接着小波动的特征，即波峰和波谷具有连续性。在高波动的时候，人们情绪高涨市场的势能不断积累，于是会转化成更大的波动；在低波动的时候，人们对市场的兴趣越来越低，市场逐渐会成为一摊死水。此外，金融事件序列存在波动的不对称性，在上涨时候的波动率会小于下跌时候的波动率。
Garch模型作为现代的金融事件序列模型，是基于波动聚集这个特性建模的。波动聚集告诉我们当前的波动率是和过去的波动率存在一定的关系，方差的概念也相应的扩展到条件方差，所谓条件反差指的是过去时刻信息已知的方差。Garch模型认为本期的条件方差是过去N期条件方差和序列平方的线性组合，而序列是本期条件方差和白噪声的乘积。
日交易量
每日交易量内发生的 变化。
plot(dj_vol)
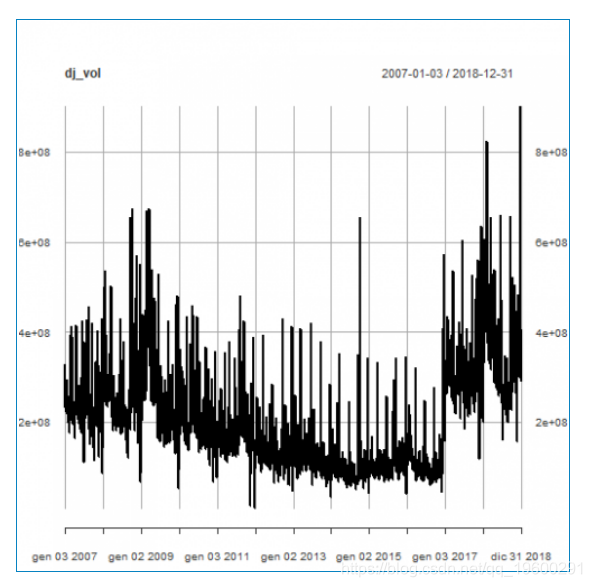
首先，我们验证具有常数均值的线性回归在统计上是显着的。
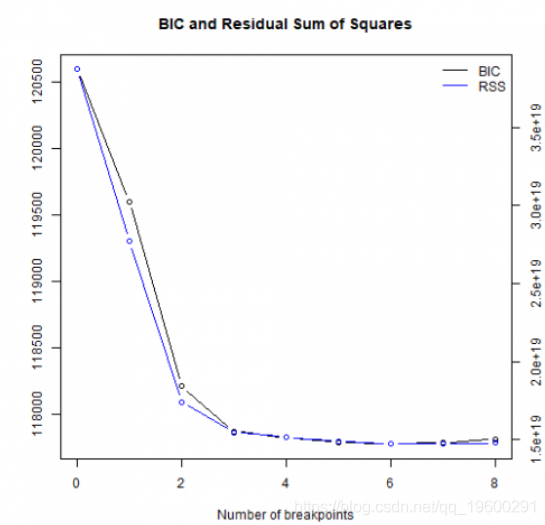
在休息时间= 6时达到最小BIC。
以下是道琼斯日均交易量与水平变化（红线） 。
plot(bb, lwd = c(3,1), col = c("red", "black"))
summary(bp_dj_vol)
##
## Optimal (m+1)-segment partition:
##
## Call:
## breakpoints.formula(formula = dj_vol ~ 1, h = 0.1)
##
## Breakpoints at observation number:
##
## m = 1 2499
## m = 2 896 2499
## m = 3 626 1254 2499
## m = 4 342 644 1254 2499
## m = 5 342 644 1219 1649 2499
## m = 6 320 622 924 1251 1649 2499
## m = 7 320 622 924 1251 1692 2172 2499
## m = 8 320 622 924 1251 1561 1863 2172 2499
##
## Corresponding to breakdates:
##
## m = 1
## m = 2 0.296688741721854
## m = 3 0.207284768211921
## m = 4 0.113245033112583 0.213245033112583
## m = 5 0.113245033112583 0.213245033112583
## m = 6 0.105960264900662 0.205960264900662 0.305960264900662
## m = 7 0.105960264900662 0.205960264900662 0.305960264900662
## m = 8 0.105960264900662 0.205960264900662 0.305960264900662
##
## m = 1
## m = 2
## m = 3 0.41523178807947
## m = 4 0.41523178807947
## m = 5 0.40364238410596 0.546026490066225
## m = 6 0.414238410596027 0.546026490066225
## m = 7 0.414238410596027 0.560264900662252
## m = 8 0.414238410596027 0.516887417218543 0.616887417218543
##
## m = 1 0.827483443708609
## m = 2 0.827483443708609
## m = 3 0.827483443708609
## m = 4 0.827483443708609
## m = 5 0.827483443708609
## m = 6 0.827483443708609
## m = 7 0.719205298013245 0.827483443708609
## m = 8 0.719205298013245 0.827483443708609
##
## Fit:
##
## m 0 1 2 3 4 5 6
## RSS 3.872e+19 2.772e+19 1.740e+19 1.547e+19 1.515e+19 1.490e+19 1.475e+19
## BIC 1.206e+05 1.196e+05 1.182e+05 1.179e+05 1.178e+05 1.178e+05 1.178e+05
##
## m 7 8
## RSS 1.472e+19 1.478e+19
## BIC 1.178e+05 1.178e+05plot(bb, lwd = c(3,1), col = c("red", "black"))
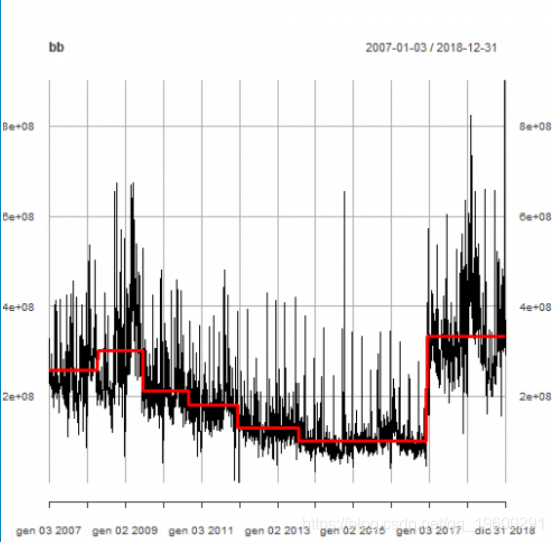
每日交易量对数比率模型
每日交易量对数比率：
plot(dj_vol_log_ratio)
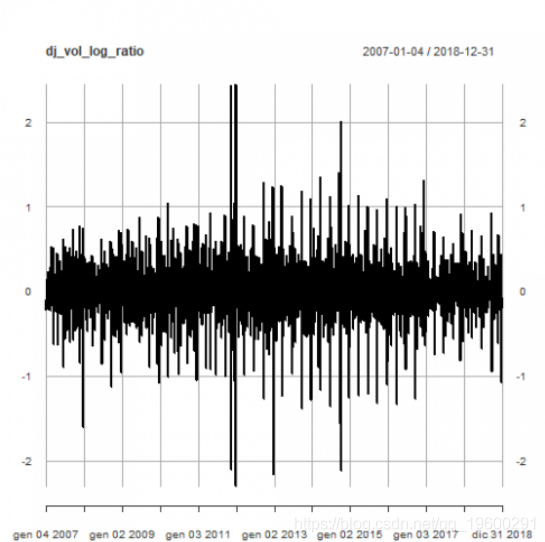
异常值检测
下面我们将原始时间序列与调整后的异常值进行比较。
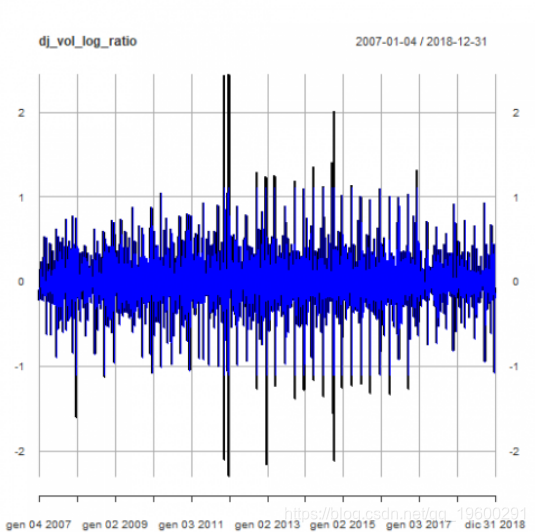
相关图
pacf(dj_vol_log_ratio)
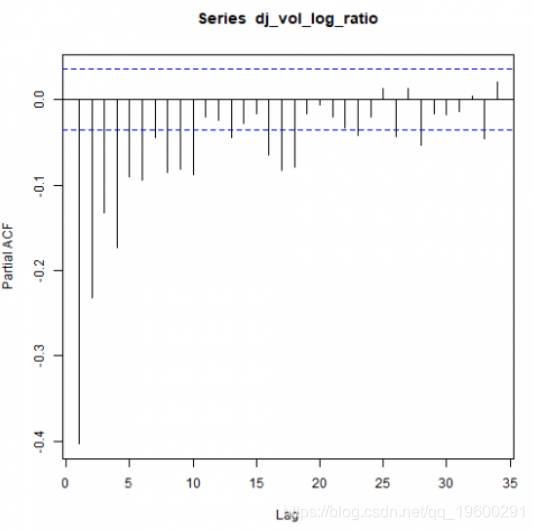
上图可能表明 ARMA（p，q）模型的p和q> 0.
单位根测试
我们 提供Augmented Dickey-Fuller测试。
根据 测试统计数据与临界值进行比较，我们拒绝单位根存在的零假设。
ARMA模型
我们现在确定时间序列的ARMA结构，以便对结果残差运行ARCH效果测试。
ma1系数在统计上不显着。因此，我们尝试使用以下ARMA（2,3）模型。
所有系数都具有统计显着性，AIC低于第一个模型。然后我们尝试使用ARMA（1,2）。
##
## Call:
## arima(x = dj_vol_log_ratio, order = c(1, 0, 2), include.mean = FALSE)
##
## Coefficients:
## ar1 ma1 ma2
## 0.6956 -1.3183 0.3550
## s.e. 0.0439 0.0518 0.0453
##
## sigma^2 estimated as 0.06598: log likelihood = -180.92, aic = 367.84
该模型在集合中具有最高的AIC，并且所有系数具有统计显着性。
我们还可以尝试 进一步验证。
eacf(dj_vol_log_ratio)
## AR / MA
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13
## 0 xooxxooxooxooo
## 1 xxoxoooxooxooo
## 2 xxxxooooooxooo
## 3 xxxxooooooxooo
## 4 xxxxxoooooxooo
## 5 xxxxoooooooooo
## 6 xxxxxoxooooooo
## 7 xxxxxooooooooo
以“O”为顶点的左上角三角形似乎位于{（1,2），（2,2），（1,3），（2,3）}之内，代表潜在的集合（ p，q）根据eacf（）函数输出的值。
我们已经在集合{（3,2）（2,3）（1,2）}内验证了具有（p，q）阶的ARMA模型。让我们试试{（2,2）（1,3）}
##
## Call:
## arima(x = dj_vol_log_ratio, order = c(2, 0, 2), include.mean = FALSE)
##
## Coefficients:
## ar1 ar2 ma1 ma2
## 0.7174 -0.0096 -1.3395 0.3746
## s.e. 0.1374 0.0560 0.1361 0.1247
##
## sigma^2 estimated as 0.06598: log likelihood = -180.9, aic = 369.8
ar2系数在统计上不显着。
##
## Call:
## arima(x = dj_vol_log_ratio, order = c(1, 0, 3), include.mean = FALSE)
##
## Coefficients:
## ar1 ma1 ma2 ma3
## 0.7031 -1.3253 0.3563 0.0047
## s.e. 0.0657 0.0684 0.0458 0.0281
##
## sigma^2 estimated as 0.06598: log likelihood = -180.9, aic = 369.8
##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 0.7030934 0.0656902 10.7032 < 2.2e-16 ***
## ma1 -1.3253176 0.0683526 -19.3894 < 2.2e-16 ***
## ma2 0.3563425 0.0458436 7.7730 7.664e-15 ***
## ma3 0.0047019 0.0280798 0.1674 0.867
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
ma3系数在统计上不显着。
ARCH效果测试
如果ARCH效应对于我们的时间序列的残差具有统计显着性，则需要GARCH模型。
我们测试候选平均模型ARMA（2,3）。
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: resid_dj_vol_log_ratio - mean(resid_dj_vol_log_ratio)
## Chi-squared = 78.359, df = 12, p-value = 8.476e-12
根据报告的p值，我们拒绝无ARCH效应的零假设。
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
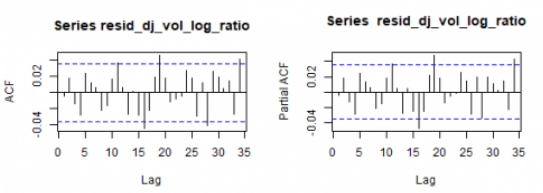
我们测试了第二个候选平均模型ARMA（1,2）。
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: resid_dj_vol_log_ratio - mean(resid_dj_vol_log_ratio)
## Chi-squared = 74.768, df = 12, p-value = 4.065e-11
根据报告的p值，我们拒绝无ARCH效应的零假设。
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
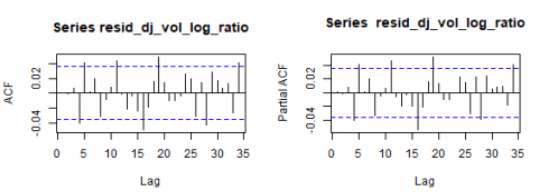
要检查 对数比率内的不对称性，将显示汇总统计数据和密度图。
## DJI.Volume
## nobs 3019.000000
## NAs 0.000000
## Minimum -2.301514
## Maximum 2.441882
## 1. Quartile -0.137674
## 3. Quartile 0.136788
## Mean -0.000041
## Median -0.004158
## Sum -0.124733
## SE Mean 0.005530
## LCL Mean -0.010885
## UCL Mean 0.010802
## Variance 0.092337
## Stdev 0.303869
## Skewness -0.182683
## Kurtosis 9.463384
plot(density(dj_vol_log_ratio))
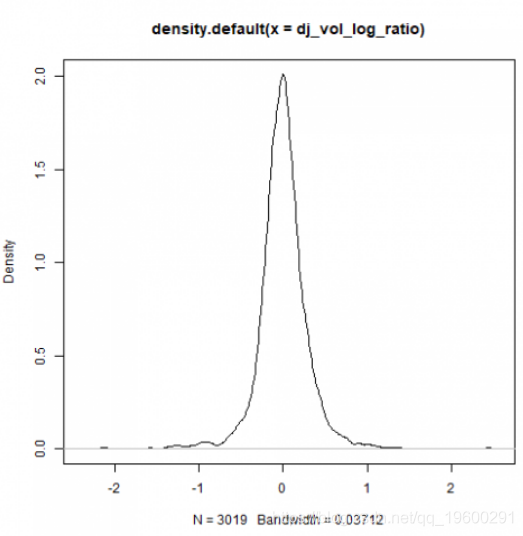
因此，对于每日交易量对数比，还将提出eGARCH模型。
为了将结果与两个候选平均模型ARMA（1,2）和ARMA（2,3）进行比较，我们进行了两次拟合
ARMA-GARCH：ARMA（1,2）+ eGARCH（1,1）所有系数都具有统计显着性。然而，基于上面报道的标准化残差p值的加权Ljung-Box检验，我们拒绝了对于本模型没有残差相关性的零假设。
ARMA-GARCH：ARMA（2,3）+ eGARCH（1,1）
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : eGARCH(1,1)
## Mean Model : ARFIMA(2,0,3)
## Distribution : sstd
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## ar1 -0.18607 0.008580 -21.6873 0.0e+00
## ar2 0.59559 0.004596 129.5884 0.0e+00
## ma1 -0.35619 0.013512 -26.3608 0.0e+00
## ma2 -0.83010 0.004689 -177.0331 0.0e+00
## ma3 0.26277 0.007285 36.0678 0.0e+00
## omega -1.92262 0.226738 -8.4795 0.0e+00
## alpha1 0.14382 0.033920 4.2401 2.2e-05
## beta1 0.31060 0.079441 3.9098 9.2e-05
## gamma1 0.43137 0.043016 10.0281 0.0e+00
## skew 1.32282 0.031382 42.1523 0.0e+00
## shape 3.48939 0.220787 15.8043 0.0e+00
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## ar1 -0.18607 0.023940 -7.7724 0.000000
## ar2 0.59559 0.022231 26.7906 0.000000
## ma1 -0.35619 0.024244 -14.6918 0.000000
## ma2 -0.83010 0.004831 -171.8373 0.000000
## ma3 0.26277 0.030750 8.5453 0.000000
## omega -1.92262 0.266462 -7.2154 0.000000
## alpha1 0.14382 0.032511 4.4239 0.000010
## beta1 0.31060 0.095329 3.2582 0.001121
## gamma1 0.43137 0.047092 9.1602 0.000000
## skew 1.32282 0.037663 35.1225 0.000000
## shape 3.48939 0.223470 15.6146 0.000000
##
## LogLikelihood : 356.4994
##
## Information Criteria
## ------------------------------------
##
## Akaike -0.22888
## Bayes -0.20698
## Shibata -0.22891
## Hannan-Quinn -0.22101
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.7678 0.38091
## Lag[2*(p+q)+(p+q)-1][14] 7.7336 0.33963
## Lag[4*(p+q)+(p+q)-1][24] 17.1601 0.04972
## d.o.f=5
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.526 0.4683
## Lag[2*(p+q)+(p+q)-1][5] 1.677 0.6965
## Lag[4*(p+q)+(p+q)-1][9] 2.954 0.7666
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 1.095 0.500 2.000 0.2955
## ARCH Lag[5] 1.281 1.440 1.667 0.6519
## ARCH Lag[7] 1.940 2.315 1.543 0.7301
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 5.3764
## Individual Statistics:
## ar1 0.12923
## ar2 0.20878
## ma1 1.15005
## ma2 1.15356
## ma3 0.97487
## omega 2.04688
## alpha1 0.09695
## beta1 2.01026
## gamma1 0.18039
## skew 0.38131
## shape 2.40996
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 2.49 2.75 3.27
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 1.4929 0.13556
## Negative Sign Bias 0.6317 0.52766
## Positive Sign Bias 2.4505 0.01432 **
## Joint Effect 6.4063 0.09343 *
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 17.92 0.5278
## 2 30 33.99 0.2395
## 3 40 44.92 0.2378
## 4 50 50.28 0.4226
##
##
## Elapsed time : 1.660402
所有系数都具有统计显着性。没有找到标准化残差或标准化平方残差的相关性。模型可以正确捕获所有ARCH效果。调整后的Pearson拟合优度检验不拒绝零假设，即标准化残差的经验分布和所选择的理论分布是相同的。然而：
*对于其中一些模型参数随时间变化恒定的Nyblom稳定性测试零假设被拒绝
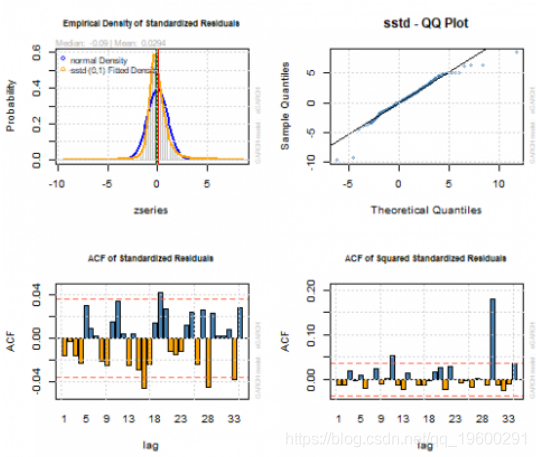
par(mfrow=c(2,2))
plot(garchfit, which=8)
plot(garchfit, which=9)
plot(garchfit, which=10)
plot(garchfit, which=11)我们用平均模型拟合（红线）和条件波动率（蓝线）显示原始道琼斯日均交易量对数时间序列。
对数波动率分析
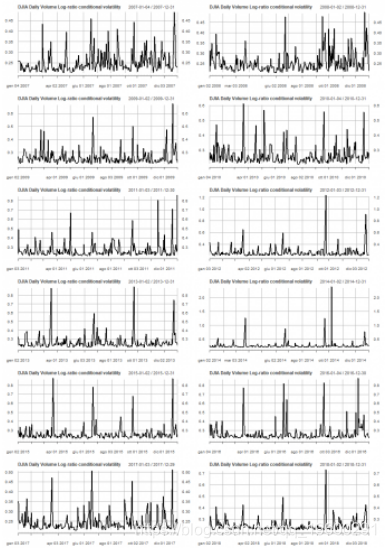
以下是我们的模型ARMA（2,2）+ eGARCH（1,1）产生的条件波动率图。
plot(cond_volatility)显示了按年度的条件波动率的线图。
par(mfrow=c(6,2))
pl <- lapply(2007:2018, function(x) { plot(cond_volatility[as.character(x)], main = "DJIA Daily Volume Log-ratio conditional volatility")})
pl
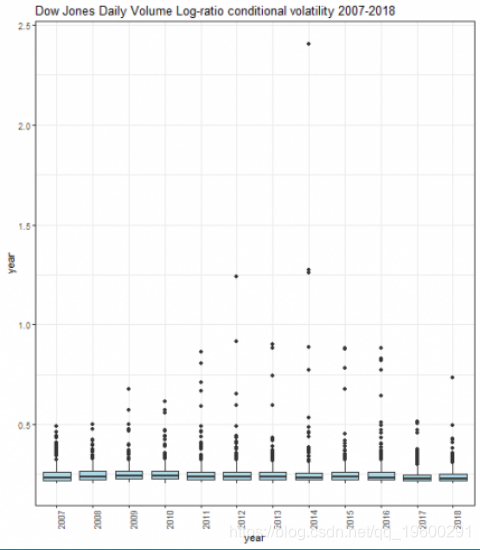
显示了按年度计算的条件波动率框图。
结论
我们研究了基本统计指标，如平均值，偏差，偏度和峰度，以了解多年来价值观的差异，以及价值分布对称性和尾部。从这些摘要开始，我们获得了平均值，中位数，偏度和峰度指标的有序列表，以更好地突出多年来的差异。
密度图可以了解我们的经验样本分布的不对称性和尾部性。
对于对数回报，我们构建了ARMA-GARCH模型（指数GARCH，特别是作为方差模型），以获得条件波动率。同样，可视化作为线和框图突出显示了年内和年之间的条件波动率变化。这种调查的动机是，波动率是变化幅度的指标，用简单的词汇表示，并且是应用于资产的对数收益时的基本风险度量。有几种类型的波动性（有条件的，隐含的，实现的波动率）。
交易量可以被解释为衡量市场活动幅度和投资者兴趣的指标。计算交易量指标（包括波动率）可以了解这种活动/利息水平如何随时间变化。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
