
我们已经很自然地认为,不仅可以用一些协变量来解释单个索赔的频率,而且可以用单个成本来解释。
当然,在考虑到一些协变量的情况下,应该考虑使用适当的族对成本的分布进行建模。以下
是我们将使用的数据集,
可下载资源
通常用来模拟成本的族是Gamma分布或逆高斯分布或对数正态分布(它不在指数族中,但是可以假设成本的对数可以用高斯分布建模)。在这里仅考虑一个协变量,例如汽车的寿命,以及两个不同的模型:一个Gamma模型和一个对数正态模型。
> age=0:20
> reggamma.sp <- glm(cout~agevehi,family=Gamma(link="log"),
+ data=couts)
> Pgamma <- predict(reggamma.sp,newdata=data.frame(agevehi=age),type="response")对于Gamma回归,这是一个简单的GLM,因此并不困难。对于对数正态分布,应该记住对数正态分布的期望值不是基础高斯分布的指数。应该进行更正,以便在这里获得平均费用的无偏估算,
我们可以在一张图上绘制这两个预测,
> plot(age,Pgamma,xlab="",ylab="",col="red",type="b",pch=4)
> lines(age,Pln,col="blue",type="b")
也可以使用样条曲线,因为年龄没有可能以可乘的方式出现在这里
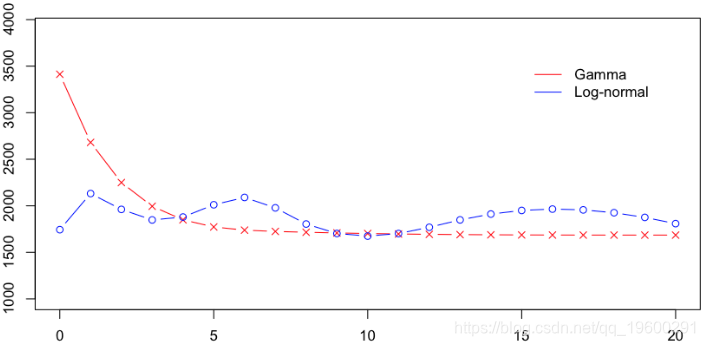
在这里,两个模型非常接近。但是,Gamma模型对大额索赔可能非常敏感。另一方面,通过对数正态模型的对数转换,可以看出该模型对大额索赔不太敏感。实际上,如果我使用完整的数据集,则回归如下:
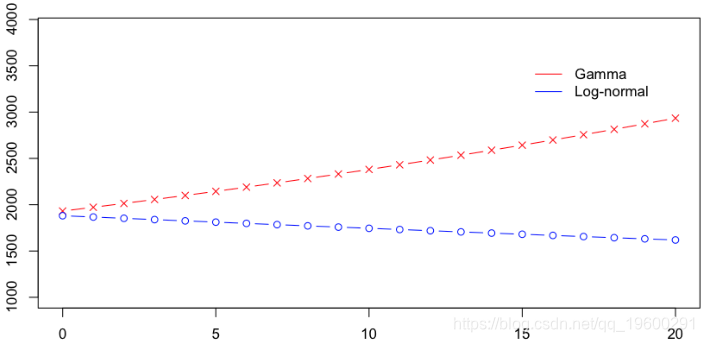
即,具有对数正态分布的平均成本随着汽车的使用年限而降低,而随着Gamma模型的增长而增加。
> couts[which.max(couts$cout),]
cout exposition zone puis agevehi ageconduct
7842 4024601 0.22 B 9 13 19
marque carbur densi region
7842 2 E 93 24一名年轻司机带着一辆13岁的汽车索赔400万美元。这是Gamma回归的异常值,显然会影响估计值(如果只有第二个,则第二大)。由于大额索赔对平均成本的估算有明显影响,因此自然的想法可能是删除那些大额索赔。或者也许将它们视为与正常索赔不同:正常索赔可以通过一些协变量来解释,但也许这些大索赔不仅应在其自己的类别内,而且应在投资组合中的所有被保险人内共享。为了使这个想法正式化,我们可以写
蓝色部分与正常大小的声明相关联,而大号部分对应于红色部分。然后,有可能进行三种回归:一个针对正常大小的索赔,一个针对大的索赔,以及一项针对具有大索赔的指标(假设发生索赔)。大笔索款超过10,000美元
> s= 10000
> couts$normal=(couts$cout<=s)
> mean(couts$normal)
[1] 0.9818087在我们的数据集中占2%的索赔。我们可以进行3组回归,并根据汽车的寿命进行平滑回归。第一个模拟大额索赔个人成本的模型,
> ypB=predict(regB,newdata=data.frame(agevehicule=age),type="response")
> ypB2=mean(couts$cout[indice])第二个模型正常索赔个人成本,
> ypA=predict(regA,newdata=data.frame(agevehicule=age),type="response")
> ypA2=mean(couts$cout[indice])最后,考虑到发生了索赔,提出了第三种索赔的可能性
> ypC=predict(regC,newdata=data.frame(agevehicule=age),type="response")
> ypC2=predict(regC2,newdata=data.frame(agevehicule=age),type="response")在下图上,我们绘制了
在这里,将Gamma回归(包括样条曲线)作为平均成本,而逻辑回归(也包括样条曲线)被视为对概率进行建模。
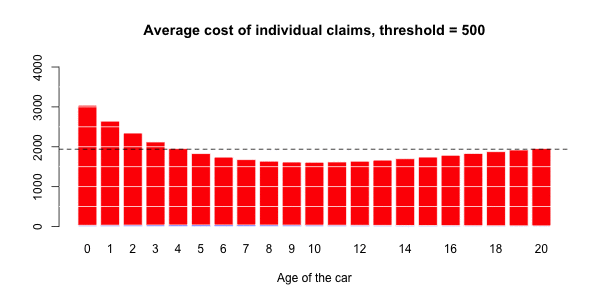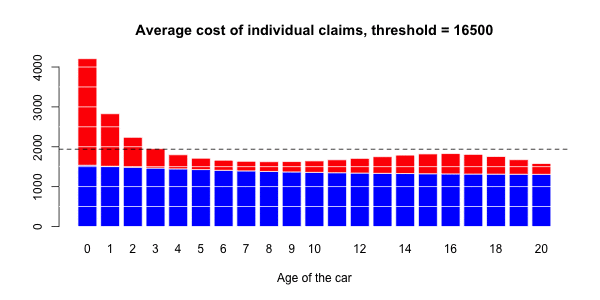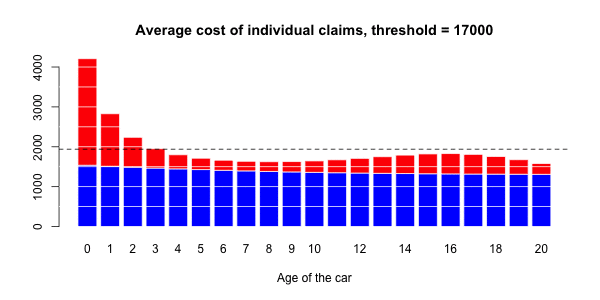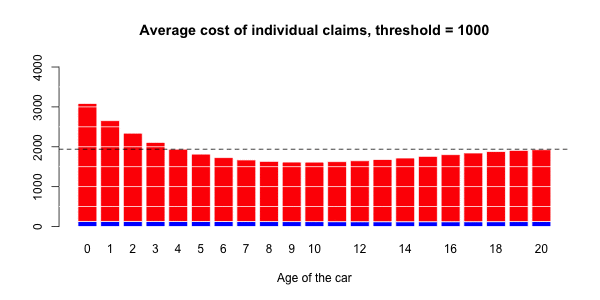
应进行调整以获得足够的溢价水平。即
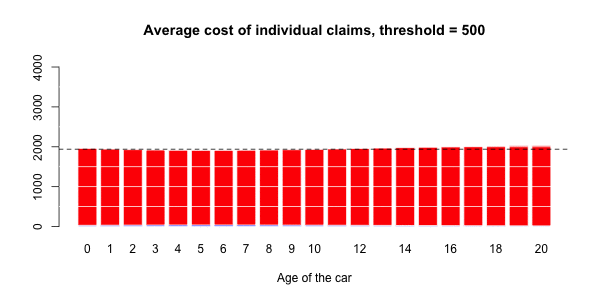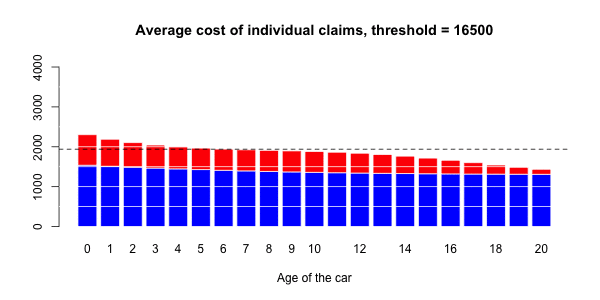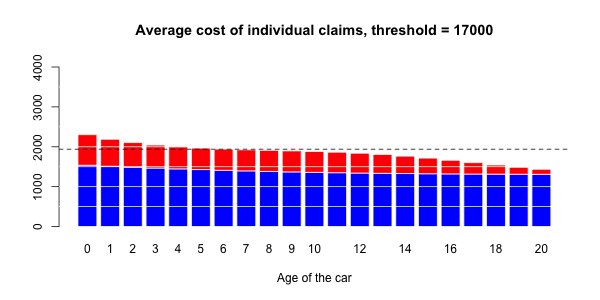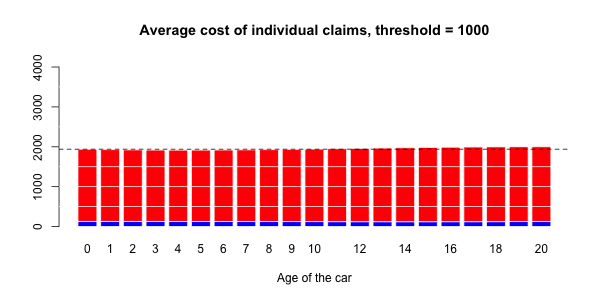
更进一步,可能还可以假设,不仅索赔的大小(假设索赔额很大)不是任何协变量的函数,而且拥有极大索赔的可能性 也不是。
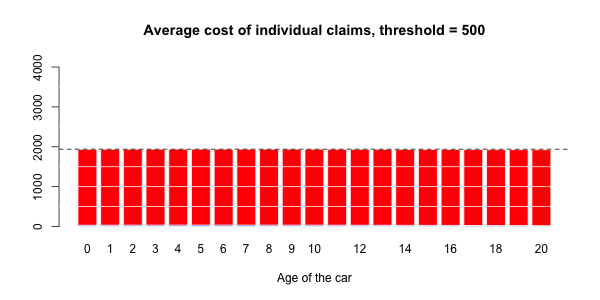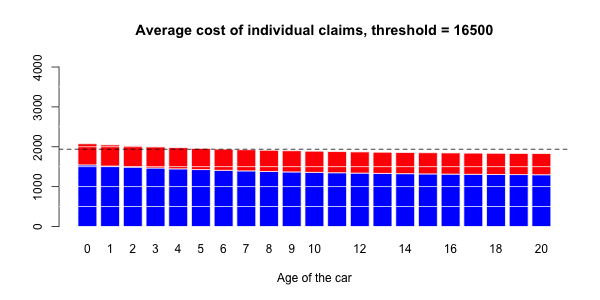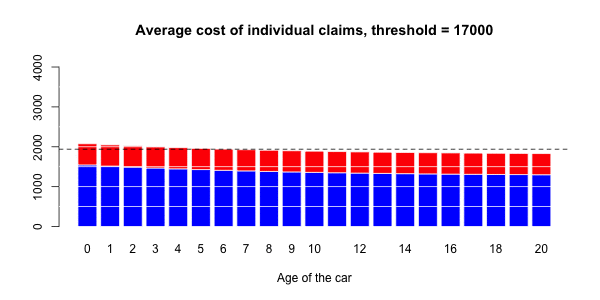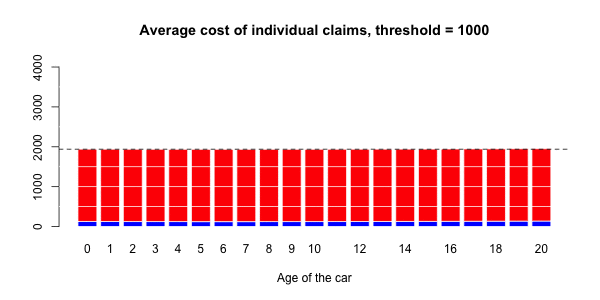
从第一部分开始,我们已经看到了所考虑的分布对预测有影响,在第二部分中,我们已经看到了大额索赔的定义(以及如何处理它们)也有影响。很明显,精算师在进行利率评估时具有一定的杠杆作用。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据


