逻辑logistic回归是研究中常用的方法,可以进行影响因素筛选、概率预测、分类等
逻辑logistic回归是研究中常用的方法,可以进行影响因素筛选、概率预测、分类等，例如医学研究中高通里测序技术得到的数据给高维变量选择问题带来挑战。
惩罚logisitc回归可以对高维数据进行变量选择和系数估计，且其有效的算法保证了计算的可行性。方法本文介绍了常用的惩罚logistic算法如LASSO、岭回归。
可下载资源
方法
我们之前已经看到，用于估计参数模型参数的经典估计技术是使用最大似然法。更具体地说，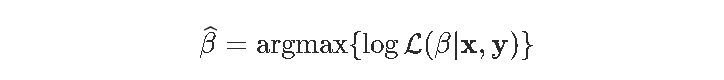
这里的目标函数只关注拟合优度。但通常，在计量经济学中，我们相信简单的理论比更复杂的理论更可取。所以我们想惩罚过于复杂的模型。
正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。
在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。
正则化一般会采用 L1 范式或者 L2 范式，其形式分别为 和
。
-
L1 正则化
LASSO 回归，相当于为模型添加了这样一个先验知识：w 服从零均值拉普拉斯分布。 首先看看拉普拉斯分布长什么样子：
由于引入了先验知识，所以似然函数这样写：
取 log 再取负，得到目标函数：
等价于原始损失函数的后面加上了 L1 正则，因此 L1 正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识。
2. L2 正则化
Ridge 回归，相当于为模型添加了这样一个先验知识：w 服从零均值正态分布。
首先看看正态分布长什么样子：
由于引入了先验知识，所以似然函数这样写：
取 ln 再取负，得到目标函数：
等价于原始的损失函数后面加上了 L2 正则，因此 L2 正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验知识。
3. L1 和 L2 的区别
从上面的分析中我们可以看到，L1 正则化增加了所有权重 w 参数的绝对值之和逼迫更多 w 为零，也就是变稀疏（ L2 因为其导数也趋 0, 奔向零的速度不如 L1 给力了）。我们对稀疏规则趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，大部分特征 x_i 都是和最终的输出 y_i 没有关系或者不提供任何信息的。在最小化目标函数的时候考虑 x_i 这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的特征权重反而会被考虑，从而干扰了对正确 y_i 的预测。L1 正则化的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些无用的特征，也就是把这些特征对应的权重置为 0。
L2 正则化中增加所有权重 w 参数的平方之和，逼迫所有 w 尽可能趋向零但不为零（L2 的导数趋于零）。因为在未加入 L2 正则化发生过拟合时，拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大，在某些很小的区间里，函数值的变化很剧烈，也就是某些 w 值非常大。为此，L2 正则化的加入就惩罚了权重变大的趋势
这主意不错。计量经济学教科书中经常提到这一点，但对于模型的选择，通常不涉及推理。通常，我们使用最大似然法估计参数，然后使用AIC或BIC来比较两个模型。Akaike（AIC）标准是基于
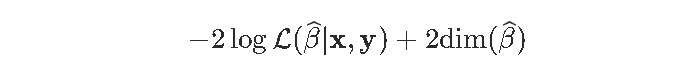
视频
Lasso回归、岭回归等正则化回归数学原理及R语言实例
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
我们在左边有一个拟合优度的度量，而在右边，该罚则随着模型的“复杂性”而增加。
这里，复杂性是使用的变量的数量。但是假设我们不做变量选择，我们考虑所有协变量的回归。定义
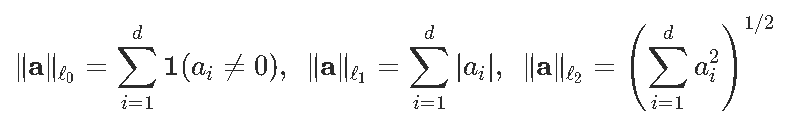
AIC是可以写为
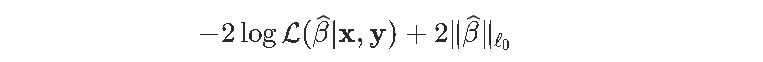
实际上，这就是我们的目标函数。更具体地说，我们将考虑
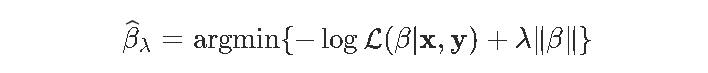
在这篇文章中，我想讨论解决这种优化问题的数值算法，对于l1（岭回归）和l2（LASSO回归）。
协变量的标准化
这里我们使用从急诊室的病人那里观察到的梗塞数据，我们想知道谁活了下来，得到一个预测模型。第一步是考虑所有协变量x_jxj的线性变换来标准化变量(带有单位方差)
for(j in 1:7) X[,j] = (X[,j]-mean(X[,j]))/sd(X[,j]) 岭回归
在运行一些代码之前，回想一下我们想要解决如下问题
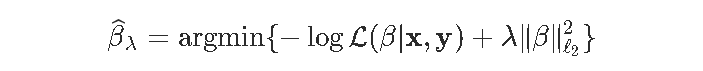
在考虑高斯变量对数似然的情况下，得到残差的平方和，从而得到显式解。但不是在逻辑回归的情况下。
岭回归的启发式方法如下图所示。在背景中，我们可以可视化logistic回归的（二维）对数似然，如果我们将优化问题作为约束优化问题重新布线，蓝色圆圈就是我们的约束：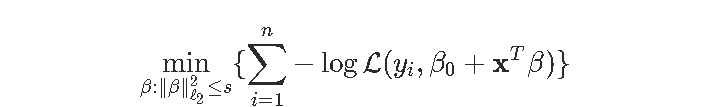
可以等效地写（这是一个严格的凸问题）
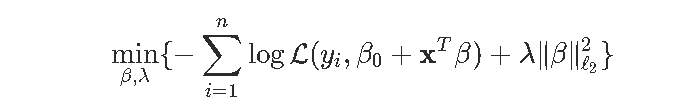
因此，受约束的最大值应该在蓝色的圆盘上
b0=bbeta[1]
beta=bbeta[-1]
sum(-y*log(1 + exp(-(b0+X%*%beta))) -
(1-y)*log(1 + exp(b0+X%*%beta)))}
u = seq(-4,4,length=251)
v = outer(u,u,function(x,y) LogLik(c(1,x,y)))
lines(u,sqrt(1-u^2),type="l",lwd=2,col="blue")
lines(u,-sqrt(1-u^2),type="l",lwd=2,col="blue")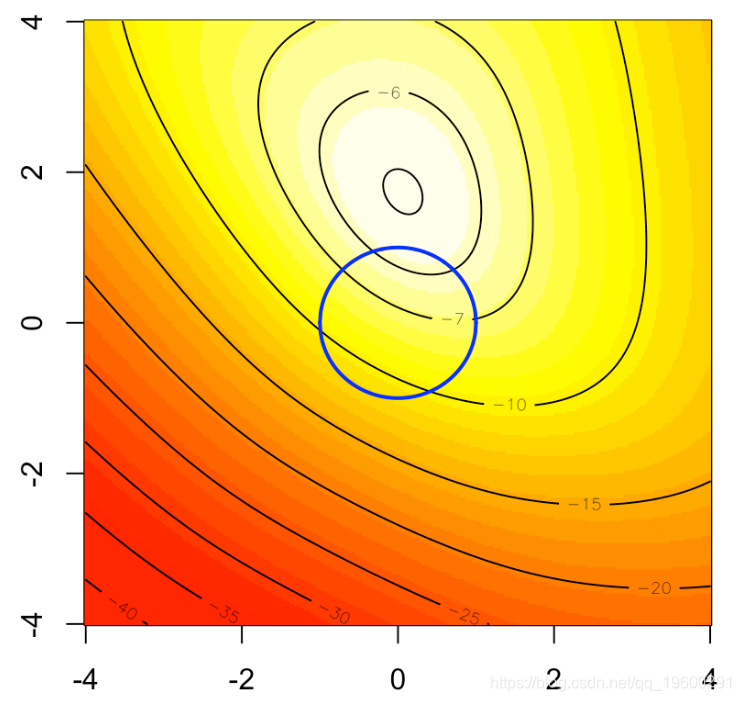
让我们考虑一下目标函数，下面的代码
-sum(-y*log(1 + exp(-(b0+X%*%beta))) - (1-y)*
log(1 + exp(b0+X%*%beta)))+lambda*sum(beta^2) 为什么不尝试一个标准的优化程序呢?我们提到过使用优化例程并不明智，因为它们强烈依赖于起点。
beta_init = lm(y~.,data=data)$coefficients
for(i in 1:1000){
vpar[i,] = optim(par = beta_init*rnorm(8,1,2),
function(x) LogLik(x,lambda), method = "BFGS", control = list(abstol=1e-9))$par}
par(mfrow=c(1,2))
plot(density(vpar[,2])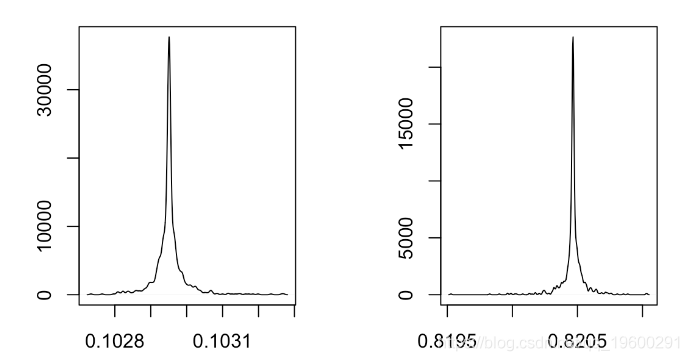 
显然，即使我们更改起点，也似乎我们朝着相同的值收敛。可以认为这是最佳的。
然后将用于计算βλ的代码
beta_init = lm(y~.)$coefficients
logistic_opt = optim(par = beta_init*0, function(x) LogLik(x,lambda),
method = "BFGS", control=list(abstol=1e-9)) 
我们可以将βλ的演化可视化为λ的函数
v_lambda = c(exp(seq(-2,5,length=61)))
plot(v_lambda,est_ridge[1,],col=colrs[1])
for(i in 2:7) lines(v_lambda,est_ridge[i,],
这看起来是有意义的:我们可以观察到λ增加时的收缩。
Ridge，使用Netwon Raphson算法
我们已经看到，我们也可以使用Newton Raphson解决此问题。没有惩罚项，算法是
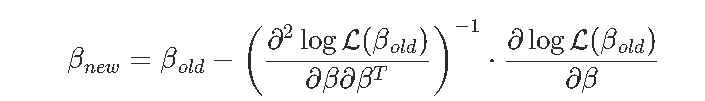
其中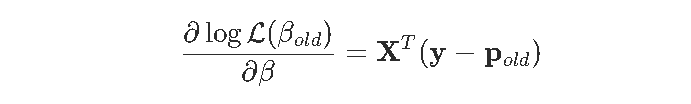
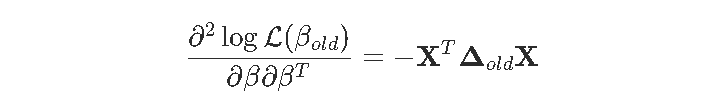
因此
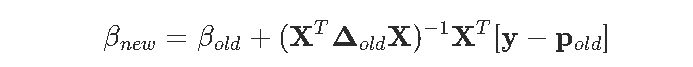
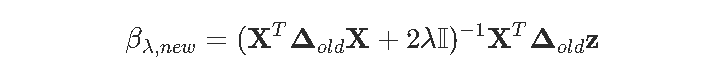
然后是代码
for(j in 1:7) X[,j] = (X[,j]-mean(X[,j]))/sd(X[,j])
for(s in 1:9){
pi = exp(X%*%beta[,s])/(1+exp(X%*%beta[,s]))
B = solve(t(X)%*%Delta%*%X+2*lambda*diag(ncol(X))) %*% (t(X)%*%Delta%*%z)
beta = cbind(beta,B)}
beta[,8:10]
[,1] [,2] [,3]
XInter 0.59619654 0.59619654 0.59619654
XFRCAR 0.09217848 0.09217848 0.09217848
XINCAR 0.77165707 0.77165707 0.77165707
XINSYS 0.69678521 0.69678521 0.69678521
XPRDIA -0.29575642 -0.29575642 -0.29575642
XPAPUL -0.23921101 -0.23921101 -0.23921101
XPVENT -0.33120792 -0.33120792 -0.33120792
XREPUL -0.84308972 -0.84308972 -0.84308972随时关注您喜欢的主题
同样，似乎收敛的速度非常快。
有趣的是，通过这个算法，我们还可以得到估计量的方差
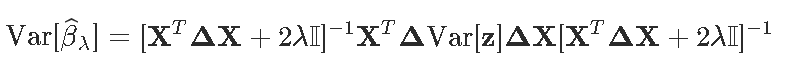
然后根据 λ函数计算 βλ的代码
for(s in 1:20){
pi = exp(X%*%beta[,s])/(1+exp(X%*%beta[,s]))
diag(Delta)=(pi*(1-pi))
z = X%*%beta[,s] + solve(Delta)%*%(Y-pi)
B = solve(t(X)%*%Delta%*%X+2*lambda*diag(ncol(X))) %*% (t(X)%*%Delta%*%z)
beta = cbind(beta,B)}
Varz = solve(Delta)
Varb = solve(t(X)%*%Delta%*%X+2*lambda*diag(ncol(X))) %*% t(X)%*% Delta %*% Varz %*%
Delta %*% X %*% solve(t(X)%*%Delta%*%X+2*lambda*diag(ncol(X))) 我们可以可视化 βλ的演化（作为 λ的函数）
plot(v_lambda,est_ridge[1,],col=colrs[1],type="l")
for(i in 2:7) lines(v_lambda,est_ridge[i,],col=colrs[i])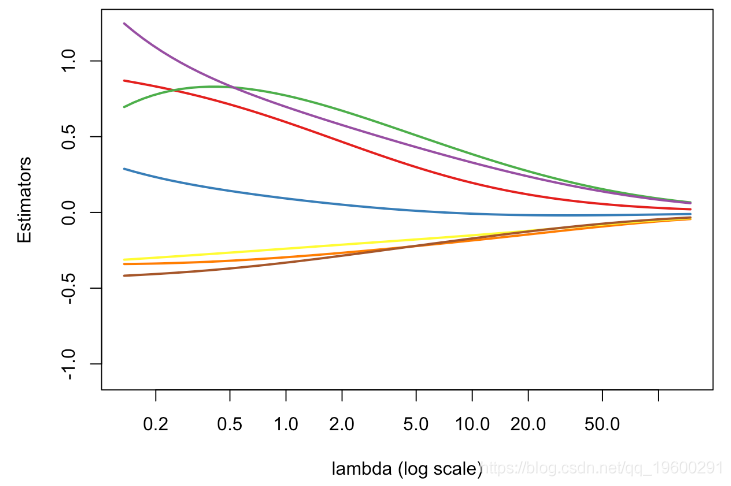
并获得方差的演变
回想一下，当λ=0（在图的左边），β0=βmco（没有惩罚）。因此，当λ增加时（i）偏差增加（估计趋于0）（ii）方差减小。
使用glmnetRidge回归
与往常一样，有R个函数可用于进行岭回归。让我们使用glmnet函数， α= 0
for(j in 1:7) X[,j] = (X[,j]-mean(X[,j]))/sd(X[,j])
glmnet(X, y, alpha=0)
plot(glm_ridge,xvar="lambda")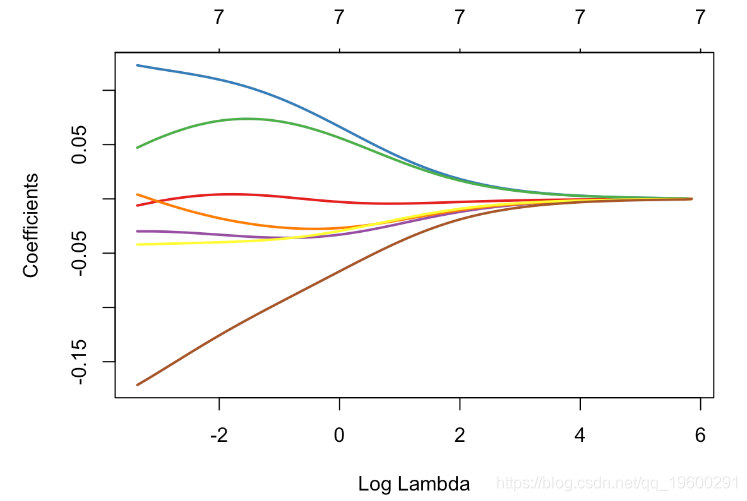
作为L1标准范数,
带正交协变量的岭回归当协变量是正交的时，得到了一个有趣的例子。这可以通过协变量的主成分分析得到。
get_pca_ind(pca)$coord让我们对这些（正交）协变量进行岭回归
glm_ridge = glmnet(pca_X, y, alpha=0)
plot(glm_ridge,xvar="lambda",col=colrs,lwd=2)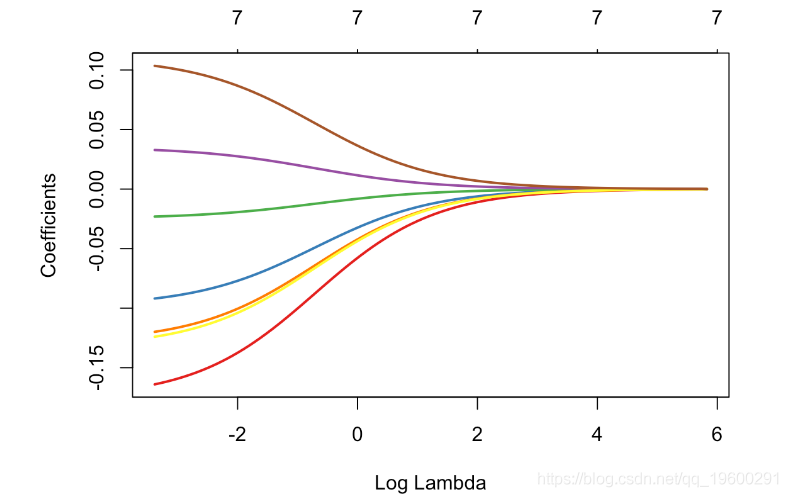
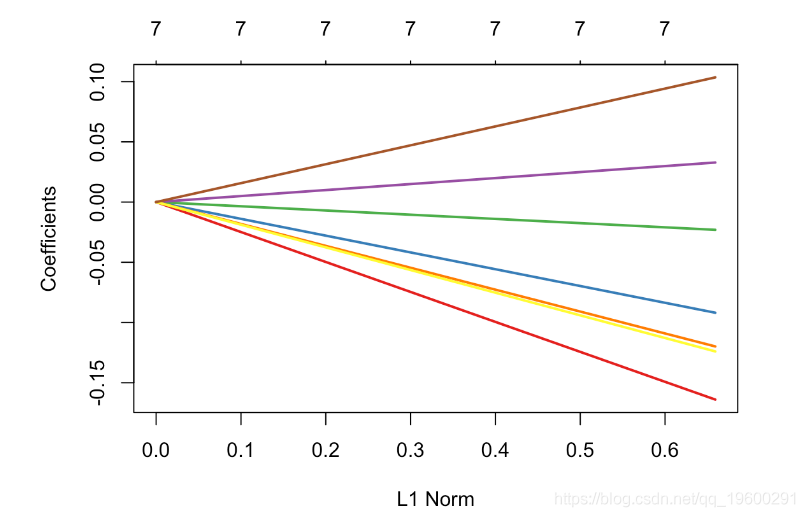
我们清楚地观察到参数的收缩，即
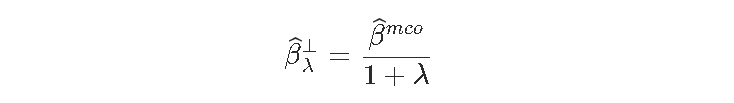
应用
让我们尝试第二组数据
我们可以尝试各种λ的值
glmnet(cbind(df0$x1,df0$x2), df0$y==1, alpha=0)
plot(reg,xvar="lambda",col=c("blue","red"),lwd=2)
abline(v=log(.2))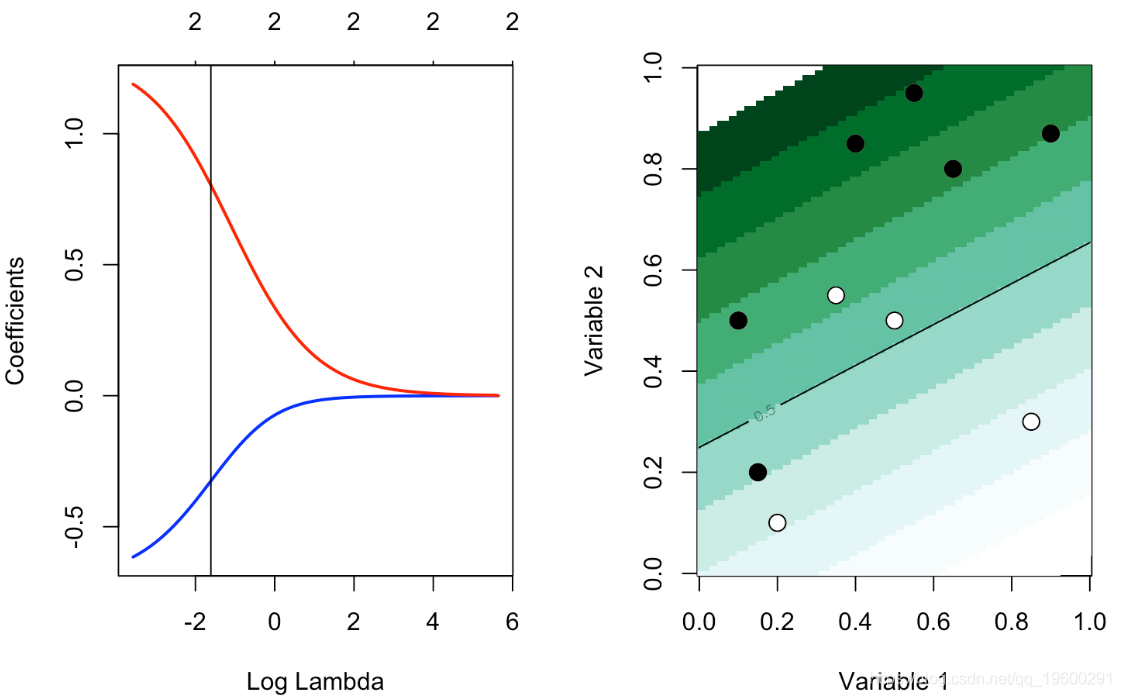 
或者
abline(v=log(1.2))
plot_lambda(1.2)下一步是改变惩罚的标准，使用l1标准范数。
协变量的标准化
如前所述，第一步是考虑所有协变量x_jxj的线性变换，使变量标准化(带有单位方差)
for(j in 1:7) X[,j] = (X[,j]-mean(X[,j]))/sd(X[,j])
X = as.matrix(X)关于lasso套索回归的启发式方法如下图所示。在背景中，我们可以可视化logistic回归的（二维）对数似然，蓝色正方形是我们的约束条件，如果我们将优化问题作为一个约束优化问题重新考虑，
岭回归
LogLik = function(bbeta){
sum(-y*log(1 + exp(-(b0+X%*%beta))) -
(1-y)*log(1 + exp(b0+X%*%beta)))}
contour(u,u,v,add=TRUE)
polygon(c(-1,0,1,0),c(0,1,0,-1),border="blue")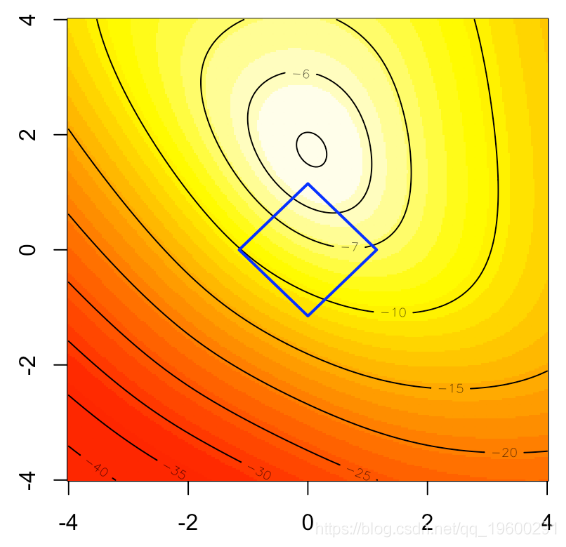
这里的好处是它可以用作变量选择工具。
启发性地，数学解释如下。考虑一个简单的回归方程y_i=xiβ+ε，具有 l1-惩罚和 l2-损失函数。优化问题变成
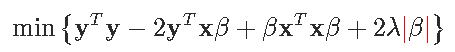
一阶条件可以写成
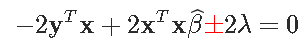
则解为
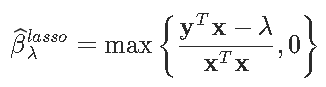
优化过程
让我们从标准（R）优化例程开始，比如BFGS
logistic_opt = optim(par = beta_init*0, function(x) PennegLogLik(x,lambda),
hessian=TRUE, method = "BFGS", control=list(abstol=1e-9))
plot(v_lambda,est_lasso[1,],col=colrs[1],type="l")
for(i in 2:7) lines(v_lambda,est_lasso[i,],col=colrs[i],lwd=2)
结果是不稳定的。
使用glmnet
为了进行比较，使用专用于lasso的R程序，我们得到以下内容
plot(glm_lasso,xvar="lambda",col=colrs,lwd=2)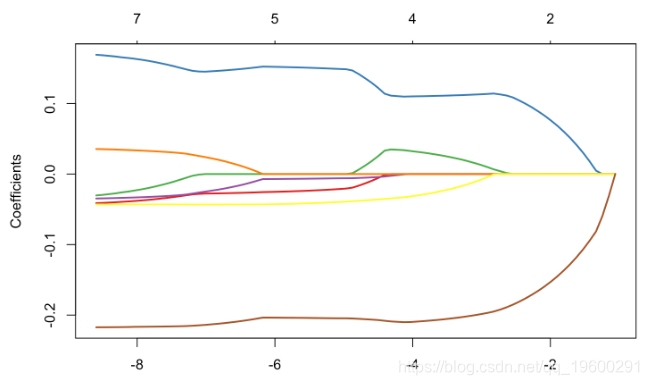
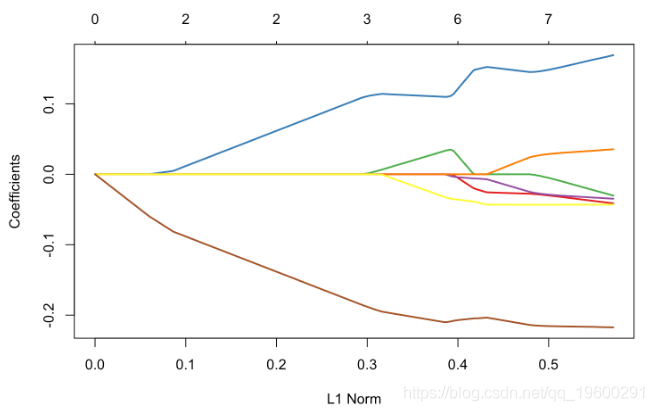
如果我们仔细观察输出中的内容，就可以看到存在变量选择，就某种意义而言，βj，λ= 0，意味着“真的为零”。
,lambda=exp(-4))$beta
7x1 sparse Matrix of class "dgCMatrix"
s0
FRCAR .
INCAR 0.11005070
INSYS 0.03231929
PRDIA .
PAPUL .
PVENT -0.03138089
REPUL -0.20962611没有优化例程，我们不能期望有空值
opt_lasso(.2)
FRCAR INCAR INSYS PRDIA
0.4810999782 0.0002813658 1.9117847987 -0.3873926427
PAPUL PVENT REPUL
-0.0863050787 -0.4144139379 -1.3849264055正交协变量
在学习数学之前，请注意，当协变量是正交的时，有一些非常清楚的“变量”选择过程，
pca = princomp(X)
pca_X = get_pca_ind(pca)$coord
plot(glm_lasso,xvar="lambda",col=colrs)
plot(glm_lasso,col=colrs)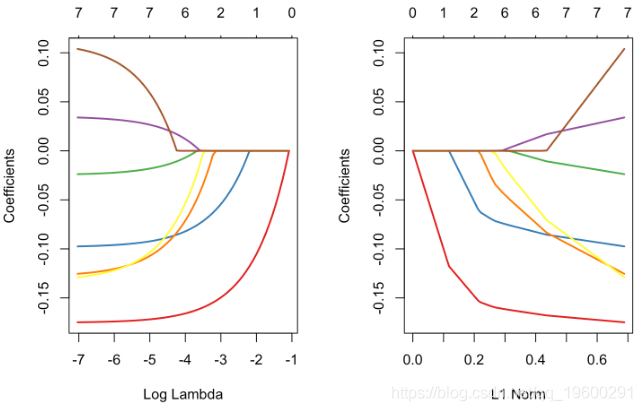
–
标准lasso
如果我们回到原来的lasso方法，目标是解决
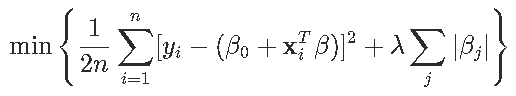
注意，截距不受惩罚。一阶条件是
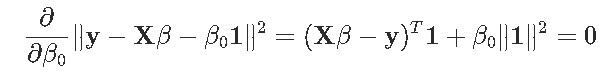
也就是
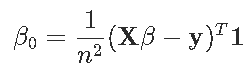
我们可以检查bf0是否至少包含次微分。
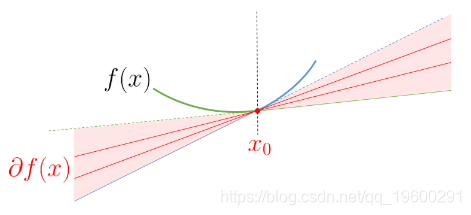
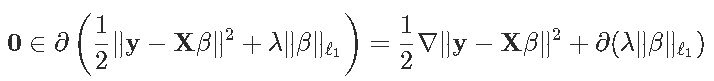
对于左边的项
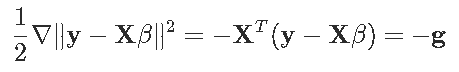
这样前面的方程就可以写出来了
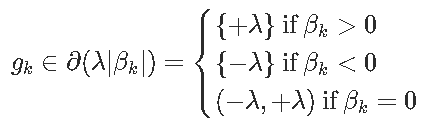
然后我们将它们简化为一组规则来检查我们的解
我们可以将βj分解为正负部分之和，方法是将βj替换为βj+-βj-，其中βj+，βj-≥0。lasso问题就变成了
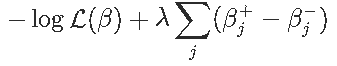
令αj+，αj−分别表示βj+，βj−的拉格朗日乘数。
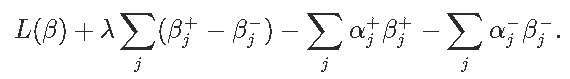
为了满足平稳性条件，我们取拉格朗日关于βj+的梯度，并将其设置为零获得
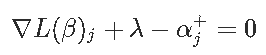
我们对βj−进行相同操作以获得
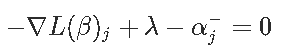
为了方便起见，引入了软阈值函数
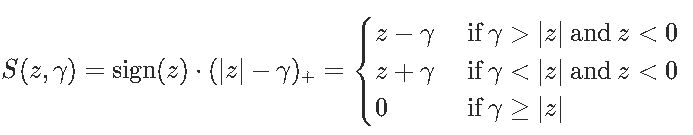
注意优化问题
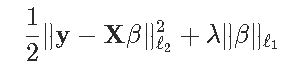
也可以写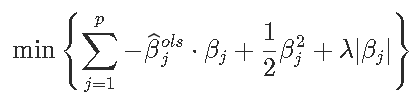
观察到
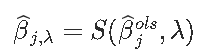
这是一个坐标更新。
现在，如果我们考虑一个（稍微）更一般的问题，在第一部分中有权重
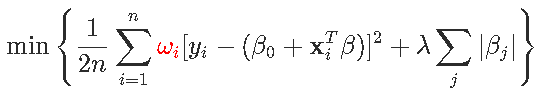
坐标更新变为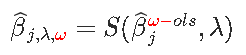
回到我们最初的问题。
lasso套索逻辑回归
这里可以将逻辑问题表述为二次规划问题。回想一下对数似然在这里
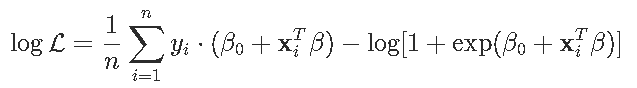
这是参数的凹函数。因此，可以使用对数似然的二次近似-使用泰勒展开，
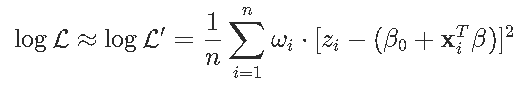
其中z_izi是
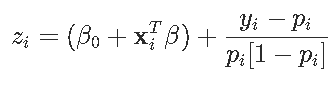
pi是预测
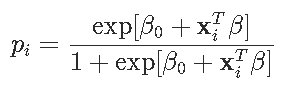
这样，我们得到了一个惩罚的最小二乘问题。我们可以用之前的方法
beta0 = sum(y-X%*%beta)/(length(y))
beta0list[j+1] = beta0
betalist[[j+1]] = beta
obj[j] = (1/2)*(1/length(y))*norm(omega*(z - X%*%beta -
beta0*rep(1,length(y))),'F')^2 + lambda*sum(abs(beta))
if (norm(rbind(beta0list[j],betalist[[j]]) -
rbind(beta0,beta),'F') < tol) { break }
}
return(list(obj=obj[1:j],beta=beta,intercept=beta0)) }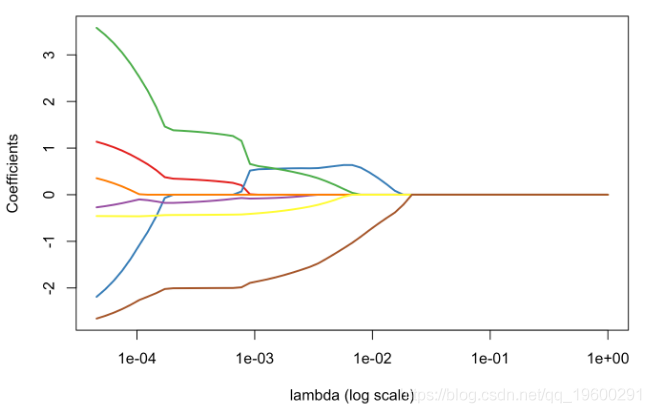
它看起来像是调用glmnet时得到的结果，对于一些足够大的λ，我们确实有空成分。
在第二个数据集上的应用
现在考虑具有两个协变量的第二个数据集。获取lasso估计的代码是
plot_l = function(lambda){
m = apply(df0,2,mean)
s = apply(df0,2,sd)
for(j in 1:2) df0[,j] &
reg = glmnet(cbind(df0$x1,df0$x2), df0$y==1, alpha=1,lambda=lambda)
u = seq(0,1,length=101)
p = function(x,y){
predict(reg,newx=cbind(x1=xt,x2=yt),type="response")}
image(u,u,v,col=clr10,breaks=(0:10)/10)
points(df$x1,df$x2,pch=c(1,19)[1+z],cex=1.5)
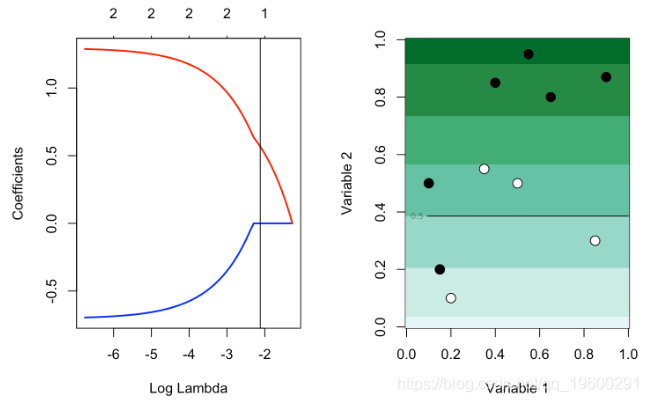
contour(u,u,v,levels = .5,add=TRUE)考虑 lambda的一些小值，我们就只有某种程度的参数缩小
plot(reg,xvar="lambda",col=c("blue","red"),lwd=2)
abline(v=exp(-2.8))
plot_l(exp(-2.8))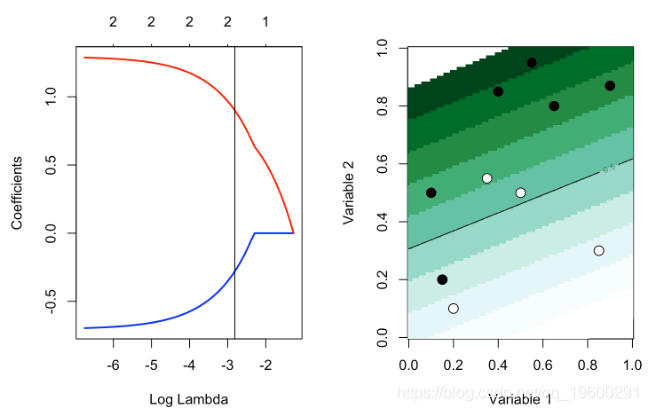
但是使用较大的λ，则存在变量选择：β1，λ= 0
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python古代文物成分分析与鉴别研究：灰色关联度、岭回归、K-means聚类、决策树分析
Python酒店预订数据：随机森林与逻辑回归模型ROC曲线可视化
Python谷歌商店Google Play APP评分预测：LASSO、多元线性回归、岭回归模型对比研究
Python糖尿病预测融合模型构建：伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
