布丰投针是几何概率领域中最古老的问题之一。

由Kaizong Ye，Sherry Deng撰写

它最早是在1777年提出的。它将针头掷到有平行线的纸上，并确定针和其中一条平行线相交的可能性。令人惊讶的结果是概率与pi的值直接相关。

R程序将根据上段所述的情况估算pi的值并使用gganimate进行动态可视化。

可下载资源

完整程序、数据和文档（word）

第1部分

对于A部分，我们创建一个数据帧，该数据帧将在3个不同的区间上生成随机值，这些区间将代表x，y的范围以及每个落针点的角度。

该问题等价于：
平面上有两条相互平行的直线，它们之间的距离为 $\alpha$ ，现在有一根长度为 $\ell$ 的针，针的一端一定在两条直线之间，问针与任意一条直线相交的概率

假设我们以左直线为原点建立坐标系，那么设针的尾部距离直线的距离为 $x$ ，以 $\ell$ 为半径作圆，尾部与圆弧的连线与垂直直线方向的夹角为 $\theta$ 。

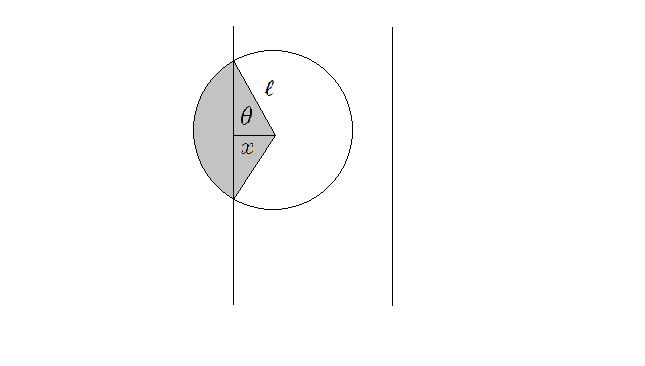
那么，针落在阴影部分内，就有交点，否则没有交点。
那么可以计算出 $\theta = arccos(\frac{x}{\ell})$ ，所以，有交点的概率 $P’$ 为
$P' = \frac{2\theta}{2\pi} = \frac{arccos(\frac{x}{\ell})}{\pi}$
在两条直线之间均匀取相距为 $\epsilon$ 的点。总点数为 $\frac{\alpha}{\epsilon}$ 则取到一个点的概率是 $\frac{\epsilon}{\alpha}$ ，从左往右编号为1 , 2 , ….. , $\frac{\alpha}{\epsilon}$

在两条直线之间均匀取相距为 $\epsilon$ 的点。总点数为 $\frac{\alpha}{\epsilon}$ ，从左往右编号为 $1 , 2 , ..... , \frac{\alpha}{\epsilon}$

考虑点 k , 一共有 $\frac{\alpha}{\epsilon}$ 个点，那么选到k点的概率是 $\frac{\epsilon}{\alpha}$ ，对于k点，与左直线有交点的概率为

$\frac{arccos(\frac{x}{\ell})}{\pi}$ 其中x 表示与左直线的距离，x大于l的时候，概率为0，因为不可能有交点。

把每个点的概率加起来，就是最后与左直线相交的概率。
所以与左直线相交的概率
$P = \sum_{k=1}^{\frac{\alpha}{\epsilon}}\frac{\epsilon}{\alpha}P'_k$

我们先计算“有机会交到直线概率的点”，没有机会的放在分母即可，总点数应该是直线长度 $\alpha$

上述过程可以抽象为：在

$y = \frac{arccos(\frac{x}{\ell})}{\pi}$

这个函数上取若干矩形，然后把这些矩形的面积加起来，

平面上的点应该是连续分布的，因为你可能会扔到任何一个位置，所以要让 $\epsilon$ 趋近于0.

而 $\epsilon$ 趋近于0时，其实就是求上述函数下方面积。因为是求面积，所以就定积分了。

这样就得到：
$P = \frac{1}{\alpha}\int_{0}^{\ell}\frac{arccos(\frac{x}{\ell})}{\pi}dx$

上面的积分表示概率之和，因为总长度为 $\alpha$ 所以要除以 $\alpha$ 这个样本总量（直线之间间距为 $\alpha$ ，点是在直线上取的）。
变形化简：
$P = \frac{1}{\alpha\pi} \lbrack \ell arccos(1) - 0 - (-\sqrt{\ell^2}) \rbrack =\frac{\ell}{\alpha\pi}$
这只是左直线的概率，所以总概率为
$\frac{2\ell}{\alpha\pi}$

这是一个易于实现的随机数情况，需要使用runif函数。此功能要求输入数量，后跟一个间隔。生成数字后，我们会将值保存到数据框中。

rneedle <- function(n) {
  x = runif(n, 0, 5) 
  y = runif(n,0, 1)
  angle = runif(n,-pi, pi) #从-180到180的角度
  values<-data.frame(cbind(x, y, angle))
  return(values)
}
values<-rneedle(50)
#检查是否生成50×3矩阵
values
#我们的数据帧已经成功生成。

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

 x           y      angle
1  4.45796267 0.312440618  1.3718465
2  3.43869230 0.462824677  2.9738367
3  2.55561523 0.596722445 -2.9638285
4  3.68098572 0.670877506 -0.6860502
5  0.03690118 0.202724803 -0.3315141
6  4.64979938 0.180091416 -0.3293093
7  4.92459238 0.172328845 -0.5221133
8  3.50660347 0.752147374  2.9100221
9  2.03787919 0.167897415 -0.3213833
10 0.38647133 0.539615776 -0.1188982
11 3.28149935 0.102886770 -1.6318256
12 3.68811892 0.765077533  1.2459037
13 1.52004894 0.682455494 -0.4219802
14 3.76151379 0.508555610  0.1082087
...

第2部分

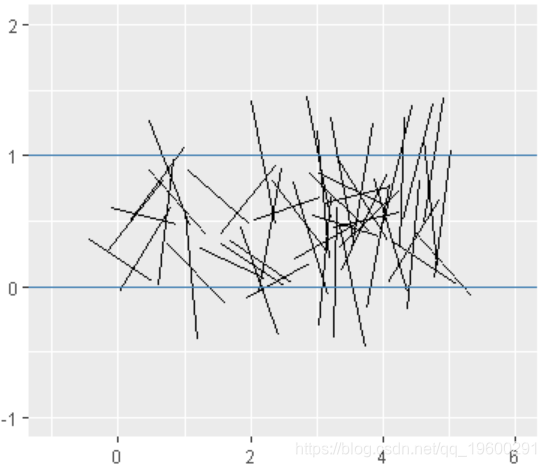
我们绘制第一部分中的针。重要的是不要在这个问题上出现超过2条水平线。它使我们可以进行检查以了解此处描绘的几何特性的一般概念。话虽如此，让我们注意我们决定在每个方向上将图形扩展1个单位。原因是想象一个针尾从y = 1开始，其角度为pi / 2。我们需要假设该方向的范围最大为2。

 plotneedle(values)

最受欢迎的见解

1.R语言动态图可视化：如何、创建具有精美动画的图

2.R语言生存分析可视化分析

3.Python数据可视化-seaborn Iris鸢尾花数据

4.r语言对布丰投针（蒲丰投针）实验进行模拟和动态

5.R语言生存分析数据分析可视化案例

6.r语言数据可视化分析案例：探索brfss数据数据分析

7.R语言动态可视化：制作历史全球平均温度的累积动态折线图动画gif视频图

8.R语言高维数据的主成分pca、 t-SNE算法降维与可视化分析案例报告

9.python主题LDA建模和t-SNE可视化

第3部分

在下面，将基于阅读布冯针和基本几何原理的知识，查看pi的估算值。

 buffon(values)

R语言动态图可视化：如何、创建具有精美动画的图

阅读文章 ➜

第4部分

运行代码后，我们收到以下答案。

buffon(X)

[1] 3.846154

set.seed(10312013)
X <- rneedle(50)
plotneedle(X)
buffon(X)

> buffon(X)
[1] 3.846154

随时关注您喜欢的主题

第5部分

如前几节所述，当我们投掷更多的针头时，我们期望以最小的不确定性获得更准确的答案。从Approxpi函数运行代码后，我们收到了平均值= 3.172314和方差0.04751391的值。对于这样一个简单的实验，它对pi进行了很高的估计。

 Approxpi(500)
mean(Approxpi(500)) 
var(Approxpi(500))

> mean(Approxpi(500)) 
[1] 3.172314
> var(Approxpi(500)) 
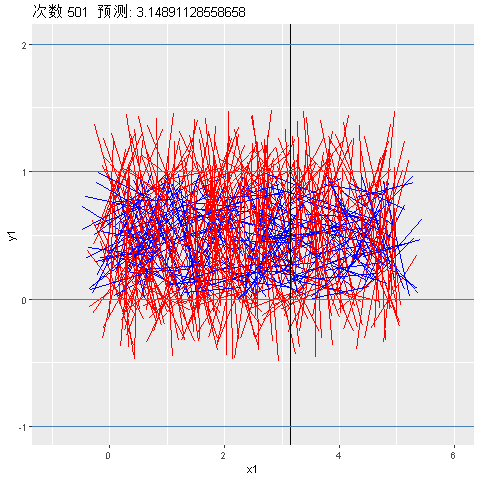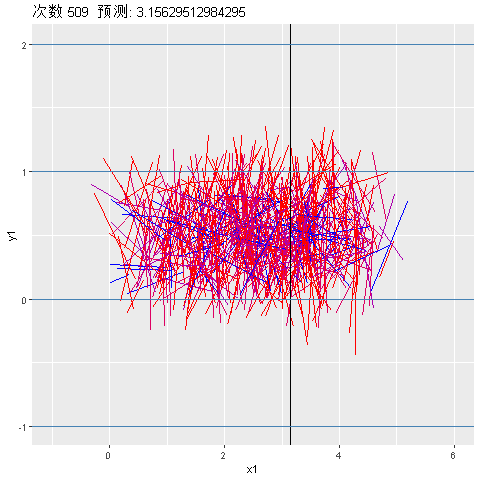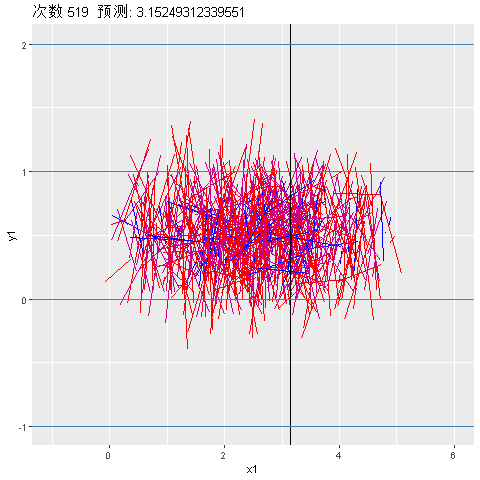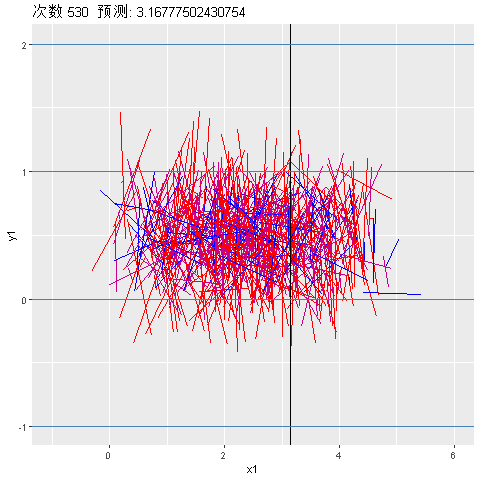
[1] 0.04751391

接下来对模拟次数从500~600的预测进行动态可视化,红色表示针投放到了直线上：

参考资料

Schroeder，L.（1974年）。布冯针问题：许多数学概念的激动人心的应用。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言对布丰投针（蒲丰投针）实验进行模拟和动态可视化生成GIF动画

布丰投针是几何概率领域中最古老的问题之一。

第1部分

第2部分

第3部分

R语言动态图可视化：如何、创建具有精美动画的图

第4部分

随时关注您喜欢的主题

第5部分

接下来对模拟次数从500~600的预测进行动态可视化,红色表示针投放到了直线上：

相关文章

R语言对布丰投针（蒲丰投针）实验进行模拟和动态可视化生成GIF动画

布丰投针是几何概率领域中最古老的问题之一。

第1部分

第2部分

第3部分

R语言动态图可视化：如何、创建具有精美动画的图

第4部分

随时关注您喜欢的主题

第5部分

接下来对模拟次数从500~600的预测进行动态可视化,红色表示针投放到了直线上：

相关文章

关注有关新文章的微信公众号