本文为非人寿保险课程的一部分，该示例对1900 -2005年间的“ 美国标准化飓风损失 ”数据集进行研究（2008）。
我们使用了广义线性模型和帕累托分布Pareto distributions分析。
可下载资源
该数据集以xls格式提供，首先我们来导入它，
数据导入和清理
> library(gdata)
> db=read.xls(data.xls",sheet=1)
excel电子表格的问题在于某些列可能具有预先指定的格式（例如，损失为000,000,000格式）
> tail(db)
Year Hurricane.Description State Category Base.Economic.Damage
202 2005 Cindy LA 1 320,000,000
203 2005 Dennis FL 3 2,230,000,000
204 2005 Katrina LA,MS 3 81,000,000,000
205 2005 Ophelia NC 1 1,600,000,000
206 2005 Rita TX 3 10,000,000,000
207 2005 Wilma FL 3 20,600,000,000
Normalized.PL05 Normalized.CL05 X X.1
202 320,000,000 320,000,000 NA NA
203 2,230,000,000 2,230,000,000 NA NA
204 81,000,000,000 81,000,000,000 NA NA
205 1,600,000,000 1,600,000,000 NA NA
206 10,000,000,000 10,000,000,000 NA NA
207 20,600,000,000 20,600,000,000 NA NA要获取我们可以使用的格式的数据，考虑以下函数，
> stupidcomma = function(x){
+ x=as.character(x)
+ for(i in 1:10){x=sub(",","",as.character(x))}
+ return(as.numeric(x))}然后将这些值转换为数字，
> base=db[,1:4]
> base$Base.Economic.Damage=Vectorize(stupidcomma)(db$Base.Economic.Damage)
> base$Normalized.PL05=Vectorize(stupidcomma)(db$Normalized.PL05)
> base$Normalized.CL05=Vectorize(stupidcomma)(db$Normalized.CL05)
从现在开始，这是我们将使用的数据集，
> tail(base)
Year Hurricane.Description State Category Base.Economic.Damage
202 2005 Cindy LA 1 3.20e+08
203 2005 Dennis FL 3 2.23e+09
204 2005 Katrina LA,MS 3 8.10e+10
205 2005 Ophelia NC 1 1.60e+09
206 2005 Rita TX 3 1.00e+10
207 2005 Wilma FL 3 2.06e+10
Normalized.PL05 Normalized.CL05
202 3.20e+08 3.20e+08
203 2.23e+09 2.23e+09
204 8.10e+10 8.10e+10
205 1.60e+09 1.60e+09
206 1.00e+10 1.00e+10
207 2.06e+10 2.06e+10数据探索
我们可以直观地看到1900年至2005年的207次飓风的成本（这里的x轴不是时间，它只是损失的指数）
> plot(base$Normalized.PL05/1e9,type="h",ylim=c(0,155))
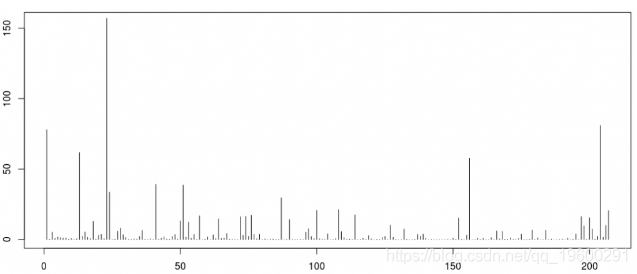
通常，计算保险合同的纯保费时有两个部分。索赔数量（或此处的飓风）以及每项索赔的个人损失。我们已经看到了个人损失，现在让我们集中讨论年度频率。
> db[88:93,]
years counts
88 2003 3
89 2004 6
90 2005 6
91 1902 0
92 1905 0
93 1907 0平均而言，我们每年大约遭受2次（主要）飓风，
> mean(db$counts)
[1] 1.95283广义线性模型预测
在预测模型中（此处，我们希望为2014年的再保险合同定价），我们可能需要考虑飓风发生频率的某些可能趋势。我们可以考虑用glm预测线性趋势或指数趋势
我们可以绘制这三个预测，并预测2014年（主要）飓风的数量，
constant linear exponential
126 1.95283 3.573999 4.379822
> points(rep((1890:2030)[126],3),prediction,col=c("black","red","blue"),pch=19)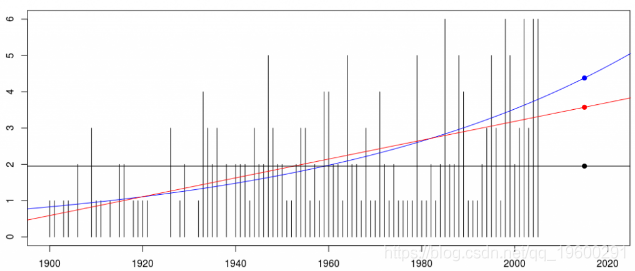
观察到改变模型将改变纯粹的溢价：如果预测不变，我们预计飓风将少于2（主要），但是随着指数趋势的发展，我们预计将超过4。
这是预期的频率。现在，我们应该找到一个合适的模型来计算再保险条约的纯保费，并具有（高）免赔额和有限（但大）赔付额。合适的模型是一个帕累托分布（见Hagstrœm（1925年）。
估计帕累托分布尾部指数
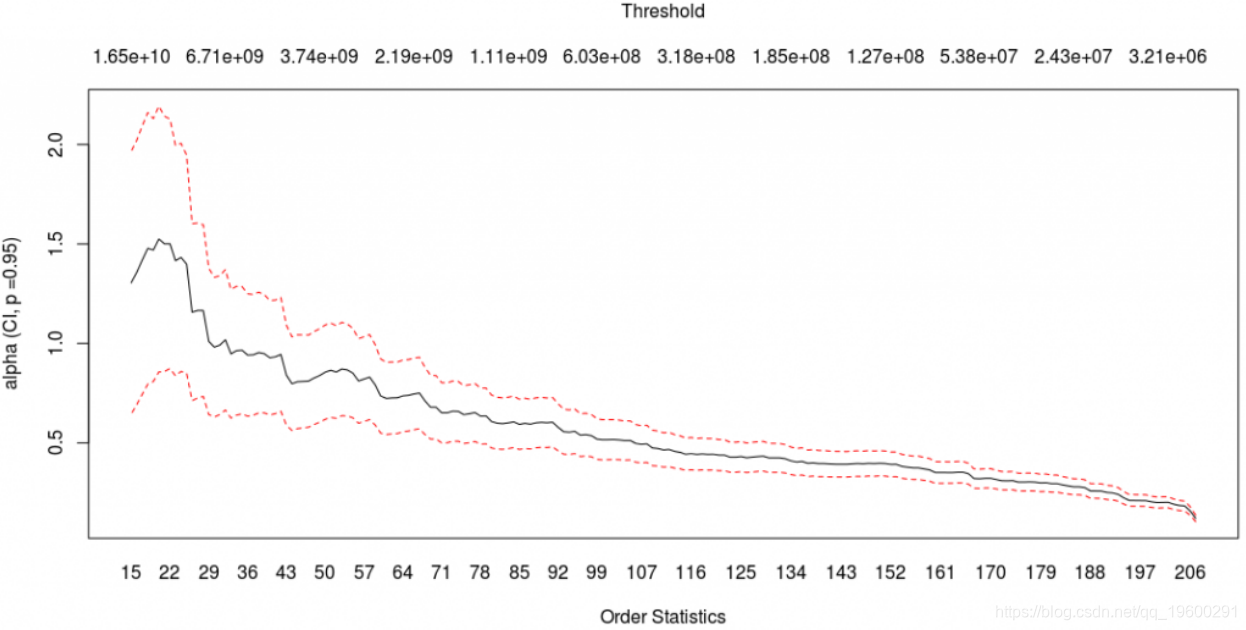
随时关注您喜欢的主题
显然，主要飓风造成的损失惨重。
现在，考虑一家拥有5％市场份额的保险公司。我们将考虑\ tilde Y_i = Y_i / 20。损失如下。考虑一个再保险条约，其免赔额为2（十亿），有限承保范围为4（十亿），
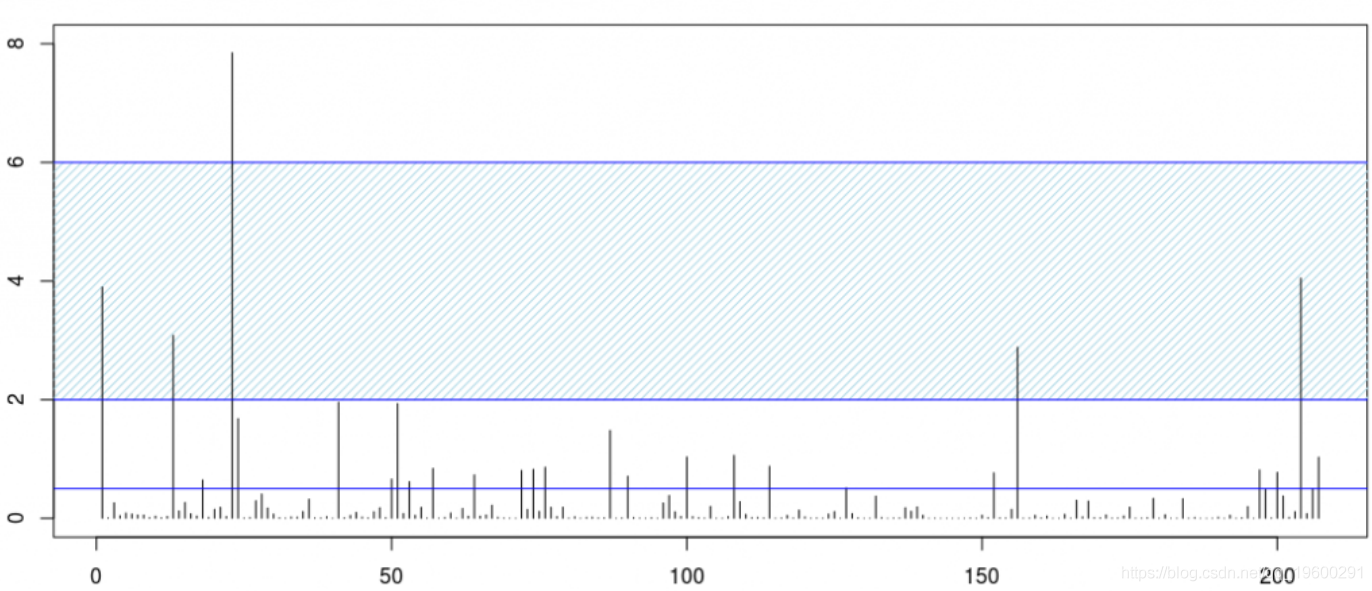
对于我们的帕累托模型，仅考虑5亿美元以上的损失，
xi beta
0.4424669 0.6705315八分之一的飓风达到了该水平
[1] 0.1256039计算再保险合同的预期价值
鉴于损失超过5亿，我们现在可以计算再保险合同的预期价值，
现在，我们预计每年的飓风会少于2（主要）
> predictions[1]
[1] 1.95283每个飓风给我们的保险公司带来超过5亿的损失的机率是12.5％，
> mean(base$Normalized.PL05/1e9/20>.5)
[1] 0.1256039并假设飓风造成的损失超过5亿美元，那么再保险公司的预期还款额（百万）
> E(2,6,gpd.PL[1],gpd.PL[2])*1e3
[1] 330.9865所以再保险合同的纯保费就是
[1] 81.18538覆盖40亿，超过2个。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【专题】2023-2024中国保险数字化营销调研报告汇总PDF洞察（附原数据表）
【专题】2024年5月金融、保险、银行行业报告汇总PDF合集分享（附原数据表）
数据分享|广义线性模型beta二项分布的淋巴结疾病风险预测可视化R语言实现
【专题】2024商业健康险与医药协同创新模式研究报告合集PDF分享（附原数据表）
