
通常,我们在回归模型中一直说的一句话是“ 请查看一下数据 ”。
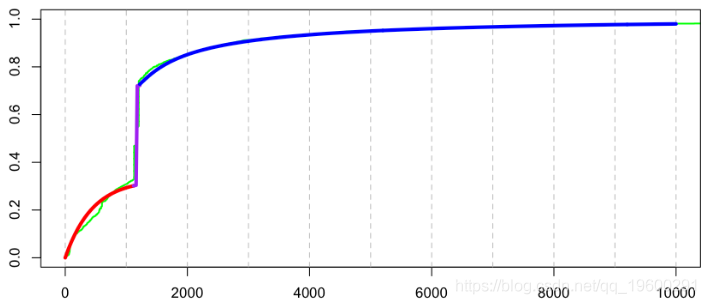
在上一篇文章中,我们没有查看数据。如果我们查看个人损失的分布,那么在数据集中,我们会看到以下内容:
可下载资源
> n=nrow(couts)
> plot(sort(couts$cout),(1:n)/(n+1),xlim=c(0,10000),type="s",lwd=2,col="green")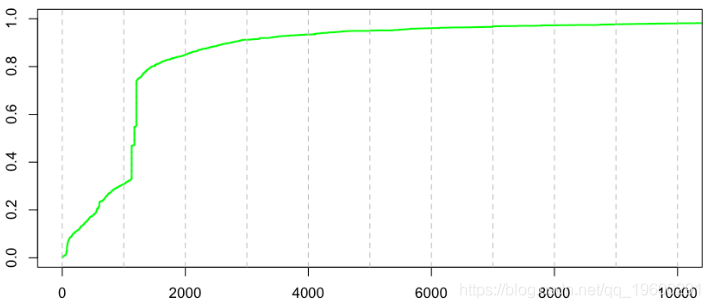
看来我们的数据库中有固定成本索赔。在标准情况下,我们如何处理?我们可以在这里使用混合分布,
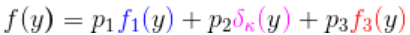
与
- 小额索赔的分布
,例如指数分布
- 狄拉克分布
,即
- 分布
,例如Gamma分布或对数正态分布
> I1=which(couts$cout<1120)
> I2=which((couts$cout>=1120)&(couts$cout<1220))
> I3=which(couts$cout>=1220)
> (p1=length(I1)/nrow(couts))
[1] 0.3284823
> (p2=length(I2)/nrow(couts))
[1] 0.4152807
> (p3=length(I3)/nrow(couts))
[1] 0.256237
> X=couts$cout
> (kappa=mean(X[I2]))
[1] 1171.998
同样,可以使用最大似然,因为
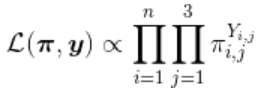
在这里,变量 (分为三个级别)分为三个指标(就像标准回归模型中的任何分类解释变量一样)。从而,
对于逻辑回归,然后使用牛顿拉夫森(Newton Raphson)算法在数值上计算最大似然。在R中,首先我们必须定义级别,例如
> couts$tranches=cut(couts$cout,breaks=seuils,
+ labels=c("small","fixed","large"))
然后,我们可以定义一个多分类logistic模型回归
使用一些选定的协变量
> formula=(tranches~ageconducteur+agevehicule+zone+carburant,data=couts)
# weights: 30 (18 variable)
initial value 2113.730043
iter 10 value 2063.326526
iter 20 value 2059.206691
final value 2059.134802
converged输出在这里
Coefficients:
(Intercept) ageconducteur agevehicule zoneB zoneC
fixed -0.2779176 0.012071029 0.01768260 0.05567183 -0.2126045
large -0.7029836 0.008581459 -0.01426202 0.07608382 0.1007513
zoneD zoneE zoneF carburantE
fixed -0.1548064 -0.2000597 -0.8441011 -0.009224715
large 0.3434686 0.1803350 -0.1969320 0.039414682
Std. Errors:
(Intercept) ageconducteur agevehicule zoneB zoneC zoneD
fixed 0.2371936 0.003738456 0.01013892 0.2259144 0.1776762 0.1838344
large 0.2753840 0.004203217 0.01189342 0.2746457 0.2122819 0.2151504
zoneE zoneF carburantE
fixed 0.1830139 0.3377169 0.1106009
large 0.2160268 0.3624900 0.1243560为了可视化协变量的影响,还可以使用样条函数
> library(splines)
> reg=(tranches~bs(agevehicule))
# weights: 15 (8 variable)
initial value 2113.730043
iter 10 value 2070.496939
iter 20 value 2069.787720
iter 30 value 2069.659958
final value 2069.479535
converged例如,如果协变量是汽车的寿命,那么我们有以下概率
> predict(reg,newdata=data.frame(agevehicule=5),type="probs")
small fixed large
0.3388947 0.3869228 0.2741825对于0到20岁的所有年龄段,
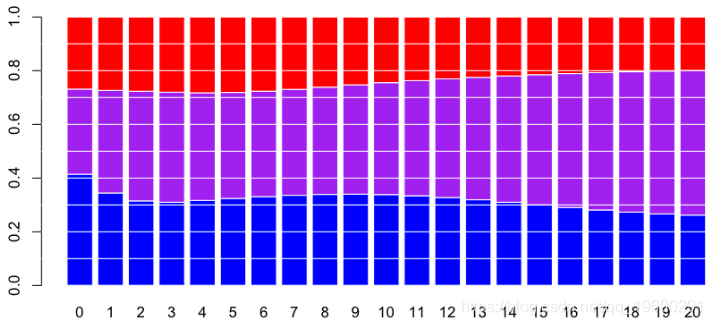
例如,对于新车,固定成本所占的比例很小(在这里为紫色),并且随着车龄的增长而不断增加。如果协变量是驾驶员居住地区的人口密度,那么我们获得以下概率
# weights: 15 (8 variable)
initial value 2113.730043
iter 10 value 2068.469825
final value 2068.466349
converged
> predict
small fixed large
0.3484422 0.3473315 0.3042263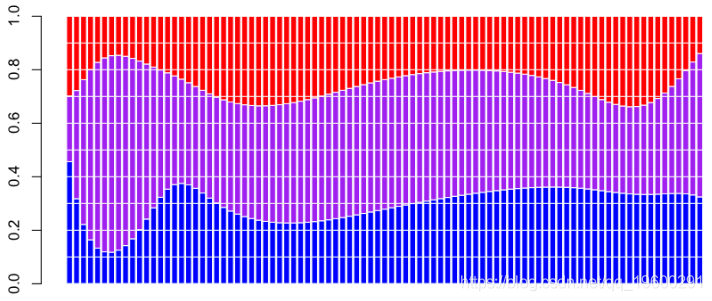
基于这些概率,可以在给定一些协变量(例如密度)的情况下得出索赔的预期成本。但首先,定义整个数据集的子集
> sbaseA=couts[couts$tranches=="small",]
> sbaseB=couts[couts$tranches=="fixed",]
> sbaseC=couts[couts$tranches=="large",]阈值由
> (k=mean(sousbaseB$cout))
[1] 1171.998然后,让我们运行四个模型,
> reg
> regA
> regB
> regC 现在,我们可以基于这些模型计算预测,
> pred=cbind(predA,predB,predC)为了可视化每个组成部分对溢价的影响,我们可以计算概率,预期成本(给定每个子集的成本),
> cbind(proba,pred)[seq(10,90,by=10),]
small fixed large predA predB predC
10 0.3344014 0.4241790 0.2414196 423.3746 1171.998 7135.904
20 0.3181240 0.4471869 0.2346892 428.2537 1171.998 6451.890
30 0.3076710 0.4626572 0.2296718 438.5509 1171.998 5499.030
40 0.3032872 0.4683247 0.2283881 451.4457 1171.998 4615.051
50 0.3052378 0.4620219 0.2327404 463.8545 1171.998 3961.994
60 0.3136136 0.4417057 0.2446807 472.3596 1171.998 3586.833
70 0.3279413 0.4056971 0.2663616 473.3719 1171.998 3513.601
80 0.3464842 0.3534126 0.3001032 463.5483 1171.998 3840.078
90 0.3652932 0.2868006 0.3479061 440.4925 1171.998 4912.379现在,可以将这些数字绘制在图形中,
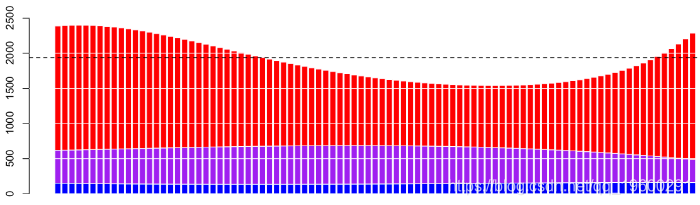
(水平虚线在我们的数据集中是索赔的平均费用)。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


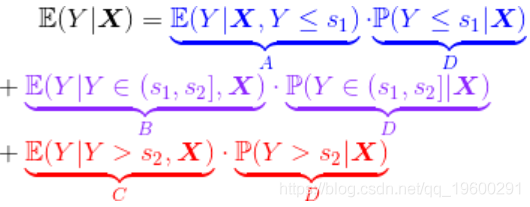
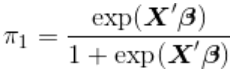
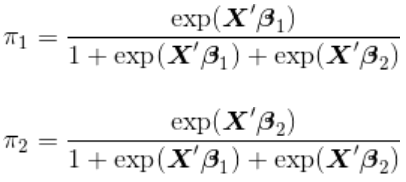
 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究 Python糖尿病预测融合模型构建:伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
Python糖尿病预测融合模型构建:伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用


