此示例演示了使用具有厚尾边缘分布的多变量copula模拟计算投资组合的风险价值和条件风险值(预期缺口)。
使用Copula仿真优化市场风险, 然后使用模拟来计算最优风险收益组合。
可下载资源
作者

内容
- 导入支持历史数据集
- 可视化标准化价格
- 边际分配
- Copula校准
- Copula模拟
- 计算单周期模拟VaR
- 组合优化
- 以给定的回报水平计算投资组合
常用的Copula函数
Copula分布作为一类连接函数,包含很多分布族,其中椭圆Copula函数族和Archimedean Copula函数族是最为常见的两个分布族。椭圆Copula函数族中主要有Gaussian Copula函数和t-Copula函数,而Archimedean Copula函数族中主要有Gumble Copula、Glayton Copula和Frank Copula函数,由于这些Copula具有厚尾的特征而在金融领域得到广泛应用。
二元Gaussian Copula的分布函数为
CGa(u,v;ρ)=∫Φ−1(u)−∞∫Φ−1(v)−∞12π1−ρ2−−−−−√exp[−s2+t2−2ρst2(1−ρ2)]dsdt , (2)
其中,
Φ−1(⋅)
是标准正态分布函数 的逆函数。
的逆函数。
自由度为 k 的二元t-Copula的分布函数为
Ct(u,v;ρ,k)=∫t−1k(u)−∞∫t−1k(v)−∞12π1−ρ2−−−−−√[1+s2+t2−2ρstk(1−ρ2)]−(k+2)/2dsdt , (3)
其中, t−1k(⋅) 是自由度为 k 的标准 t 分布函数 tk(⋅) 的逆函数。
二元Gumble Copula、Clayton Copula、Frank Copula的分布函数分别为
CGu(u,v;α)=exp{−[(−lnu)α+(−lnv)α]1α};
CCl(u,v;α)=(u−α+v−α−1)−1α,0≤u,v≤1; (4)
CF(u,v;α)=−1αln(1+(1−e−αu)(1−e−αv)1−e−α),0≤u,v≤1.
基于Copula函数的相关性度量
Copula函数作为刻画变量间相依性结构的工具,在度量具有非线性关系的变量之间的相依性结构时具有明显的优势,因此产生了一系列基于Copula函数的相关性度量。基于Copula函数的度量包括Kendall’s τ ,Spearman’s ρS ,尾部相关系数 λ 等。
1) Kendall秩相关系数
令 (X,Y) 和 (X′,Y′) 是独立同分布的随机变量,若 (X−X′)(Y−Y′)>0 ,称 (X,Y) 和 (X′,Y′) 是一致的;若 (X−X′)(Y−Y′)<0 则称 (X,Y) 和 (X′,Y′) 是不一致的。
Kendall’s秩相关系数 τ 的一般形式为:
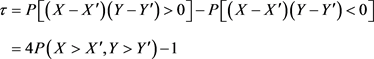
若随机变量 X,Y 的边缘分布分别为 F(x),G(y) ,相应的Copula函数为 C(u,v) ,则Kendall’s秩相关系数 τ 可由相应的Copula函数 C(u,v) 给出:
τ =4∫[0,1]2C(u,v)dC(u,v)−1 .
2) Spearman’s秩相关系数 ρS
设 (X1,Y1),(X2,Y2),(X3,Y3) 独立同分布的随机变量,Spearman’s秩相关系数 ρS 的一般形式为:

若随机变量 X,Y 的边缘分布分别为 F(x),G(y) ,相应的Copula函数为 C(u,v) ,则Spearman’s秩相关系数 ρS 可由相应的Copula函数 C(u,v) 给出:
ρS=12∫[0,1]2C(u,v)dudv−3
3) 尾部相关系数 λ
尾部相关性是人们在金融风险中比较关心的,包括上尾相关和下尾相关。令 X,Y 为连续的随机变量,具有边缘分布 F(x),G(y) 和Copula函数为 C(u,v) ,如果
limu→1−C¯¯¯(u,u)/(1−u)=λU
存在, λU∈(0,1] , C¯¯¯(u,v)=1−u−v+C(u,v) 为生存Copula函数,则称 X,Y 上尾相关; λU=0 时,称 X,Y 在分布上尾渐近独立。同样地,如果
limu→0+C(u,u)/u=λL
存在, λL∈(0,1] 时,则称 X,Y 下尾相关; λL=0 时,称 X,Y 在分布下尾渐近独立。我们把 λU,λL 统称为尾部相关系数,且 λU,λL≥0 。
导入支持历史数据集
使用API导入我们将在本练习中建模的不同资产类别的市场数据
- SPY:标准普尔500指数
- EEM:新兴市场股票
- TLT:20年期国债(iShares Barclays)
- COY:美国高收益债券
- gsp:大宗商品(iPath S&P GSCI总回报指数)
- RWR:房地产(房地产投资信托指数)
names = { 'SPY','EEM','TLT','COY','GSP','RWR' };
startPeriod = '2009-10-01' ;
endPeriod = '2013-06-24' ;
可视化标准化价格
该图显示了每个指数的相对价格走势。每个指数的初始水平已经标准化为统一,以便于比较历史记录中的相对表现。
plot(date,normPrices),datetick('x'),xlabel('Date'),ylabel('Index Value');
title('Normalized Daily Index Closings');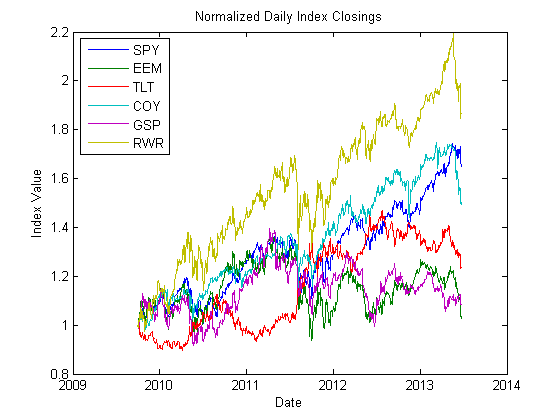
边际分布
为准备copula建模,单独描述每个指数的回报分布。虽然每个回归序列的分布可以参数化地表征,但是使用具有广义Pareto尾部的分段分布来拟合半参数模型是有用的。这使用极值理论来更好地表征每个尾部的行为。
return = price2ret( );
以下代码段为每个索引返回系列创建一个paretotails类型的对象。这些Pareto尾部对象封装参数Pareto下尾部,非参数内核平滑内部和参数Pareto上尾部的估计,以为每个索引构建复合半参数CDF。
tailFraction = 0.1;
marginal {i} = paretotails(return(:,i),tailFraction,1 - tailFraction,'kernel');SPY的边际分布:
分段分布有3个部分
-Inf <x <-0.0125822(0 <p <0.1):下尾,GPD(0.0380262,0.0084794)
-0.0125822 <x <0.01286(0.1 <p <0.9):内插内核平滑cdf
0.01286 <x <Inf(0.9 <p <1):上尾,GPD(0.0511828,0.00671413)
EEM的边际分布:
分段分布有3个部分
-Inf <x <-0.0186259(0 <p <0.1):下尾,GPD(-0.00289033,0.0126097)
-0.0186259 <x <0.0185703(0.1 <p <0.9):内插内核平滑cdf
0.0185703 <x <Inf(0.9 <p <1):上尾,GPD(0.0326916,0.00981892)
TLT的边际分布:
分段分布有3个部分
-Inf <x <-0.0132814(0 <p <0.1):下尾,GPD(0.137056,0.00414294)
-0.0132814 <x <0.0128738(0.1 <p <0.9):内插内核平滑cdf
0.0128738 <x <Inf(0.9 <p <1):上尾,GPD(0.027114,0.00583448)
COY的边际分布:
分段分布有3个部分
-Inf <x <-0.0105025(0 <p <0.1):下尾,GPD(0.47441,0.00485515)
-0.0105025 <x <0.011195(0.1 <p <0.9):内插内核平滑cdf
0.011195 <x <Inf(0.9 <p <1):上尾,GPD(0.177151,0.00500233)
GSP的边际分布:
分段分布有3个部分
-Inf <x <-0.0161561(0 <p <0.1):下尾,GPD(-0.0382412,0.0103328)
-0.0161561 <x <0.016506(0.1 <p <0.9):内插内核平滑cdf
0.016506 <x <Inf(0.9 <p <1):上尾,GPD(-0.134845,0.00778651)
RWR的边际分布:
分段分布有3个部分
-Inf <x <-0.0172097(0 <p <0.1):下尾,GPD(-0.00540337,0.0114245)
-0.0172097 <x <0.0168041(0.1 <p <0.9):内插内核平滑cdf
0.0168041 <x <Inf(0.9 <p <1):上尾,GPD(0.0302092,0.0117143)
得到的分段分布对象允许在CDF内部进行插值并在每个尾部进行外推(函数评估)。外推允许估计历史记录之外的分位数,这对于风险管理应用是非常宝贵的。在这里,我们将paretoTail分布产生的拟合与正态分布的拟合进行比较。
index = 1;
dist = marginal {index};
CLF
h = probplot(gca,@ dist.cdf);
set(h,'Color','r');
title([ 'Semi-Parametric / Piecewise Probability Plot:' names {index}])

Copula拟合
我们使用统计工具箱功能来校准和模拟数据。
使用每日索引返回,使用函数copulafit估计高斯和t copula的参数。由于在标量自由度参数(DoF)变得无限大时,copula变为高斯copula,因此两个copula实际上属于同一族,因此共享线性相关矩阵作为基本参数。
统计工具箱软件提供了两种在copula校准的技术:以下代码段首先通过上面导出的分段半参数CDF将每日居中的回报转换为均匀变量。然后它将Gaussian和t copula拟合到转换后的数据:
[〜,ax] = plotmatrix(U); title('拟合Copula之前的转换回报');


估算copula的参数。注意从t copula校准获得的相对较低的自由度参数,表明明显偏离高斯情况。
[rho,DoF] = copulafit('t',U,'ApproximateML')
rhoT =
1 0.88229 -0.59693 0.40875 0.58027 0.81485
0.88229 1 -0.52371 0.38906 0.63175 0.73608
-0.59693 -0.52371 1 -0.28404 -0.37285 -0.43114
0.40875 0.38906 -0.28404 1 0.2953 0.36207
0.58027 0.63175 -0.37285 0.2953 1 0.47097
0.81485 0.73608 -0.43114 0.36207 0.47097 1
DoF =
9.5014
估计的相关矩阵与线性相关矩阵相似但不相同
corrcoef(return) 每日收益的%线性相关矩阵
ans =
1 0.89745 -0.61065 0.4677 0.59174 0.83717
0.89745 1 -0.54167 0.45612 0.63322 0.76712
-0.61065 -0.54167 1 -0.30377 -0.3918 -0.44429
0.4677 0.45612 -0.30377 1 0.33312 0.43525
0.59174 0.63322 -0.3918 0.33312 1 0.49161
0.83717 0.76712 -0.44429 0.43525 0.49161 1
Copula模拟
现在已经估计了copula参数,使用copularnd函数模拟联合依赖的均匀变量。
然后,通过外推Pareto尾部并对平滑后的内部进行插值,通过每个索引的逆CDF 将从copularnd导出的均匀变量转换为每日居中返回。这些模拟的居中回报与从历史数据集获得的回归一致。假设回报在时间上是独立的,但在任何时间点都具有由给定的copula引起的依赖性和等级相关性。
nPoints = 10000; %#模拟观测值

计算单周期模拟VaR
来自copula模型的多变量模拟可用于计算样本组合的风险值和预期不足(CVaR)。
%样本组合组件权重
wts = [.1 .2 .3 .2 .1 .1]';
%从模拟组件返回生成组合返回
portReturns = R * wts;
%计算VaR
var = -prctile(portReturns,1);
cvar = -mean(portReturns(portReturns <-var));
%与正态分布比较
R2 = mvnrnd(mean(returns),cov(returns),10000);
normReturns = R2 * wts;
var2 = -prctile(normReturns,1);
cvar2 = -mean(normReturns(normReturns <-var2));
disp('Copula Value-at-Risk ----------------------');
fprintf('99 %% VaR:%0.2f %% \ n99 %% CVaR:%0.2f %% \ n \ n',var * 100,cvar * 100);
disp('多变量正常风险值---------');
fprintf('99 %% VaR:%0.2f %% \ n99 %% CVaR:%0.2f %% \ n \ n',var2 * 100,cvar2 * 100);
Copula风险价值----------------------
99%的风险价值:1.78%
99%CVaR:2.58%
多变量正常风险值---------
99%VaR:1.49%
99%CVaR:1.71%
组合优化
以前,我们使用模拟回报来计算样本组合的风险。相反,我们可以找到一个最佳投资组合(权重),为我们提供一定的回报风险。我们可以使用PortfolioCVaR框架来完成此任务。
p = PortfolioCVaR('ProbabilityLevel',。99,'AssetNames',名称);
p = p.setScenarios(R);
portRet = p.estimatePortReturn(wts);
CLF
visualizeFrontier(p,portRisk,portRet);
以给定的回报水平计算投资组合
wt = p.estimateFrontierByReturn(.05 / 100);
TOC;
pRisk = p.estimatePortRisk(wt);
pRet = p.estimatePortReturn(wt);
经过的时间是0.635017秒。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略
Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略 Python+AI提示词用贝叶斯方法Copula进行参数推断可视化|附数据代码
Python+AI提示词用贝叶斯方法Copula进行参数推断可视化|附数据代码



