风险价值（VaR）及其所有相关问题仍然是风险管理中的主要模型。
风险价值的一个关键问题是它没有适当地考虑波动率，这意味着危机期间风险被低估。
可下载资源
解决这个问题的一个强有力的方法是将VaR与GARCH模型结合起来考虑条件波动性。为了说明这种方法，我们将一个正态分布的GARCH（1,1）应用于股票市场指数。
##安装读取软件包
library(ggplot2)
#输入
from = "1995-11-20"
to = "2015-12-17"
symbol = "^SSMI"
#获取数据
TS <- yahooSeries(symbol, from = from, to = to)
SMI <- TS[,ncol(TS)]
SMI <- returns(SMI, method = "continuous")
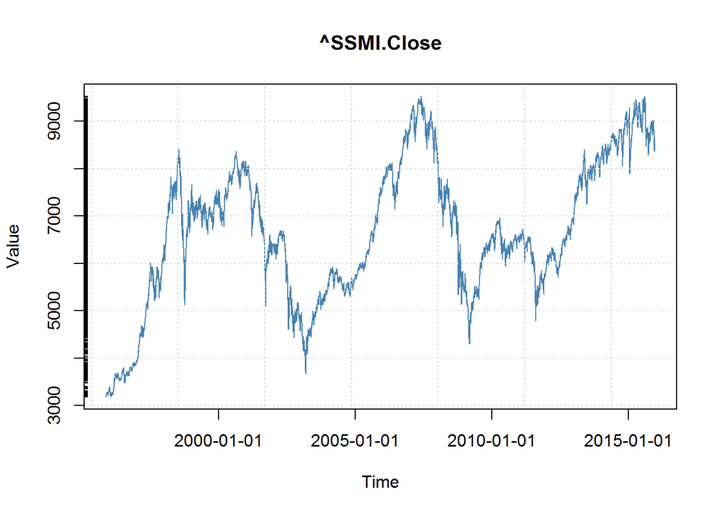
#绘制收益率
seriesPlot(TS[,4])VaR的应用主要体现在：
第一，用于风险控制。目前已有超过1000家的银行、保险公司、投资基金、养老金基金及非金融公司采用VaR方法作为金融衍生工具风险管理的手段。利用VaR方法进行风险控制，可以使每个交易员或交易单位都能确切地明了他们在进行有多大风险的金融交易，并可以为每个交易员或交易单位设置VaR限额，以防止过度投机行为的出现。如果执行严格的VaR管理，一些金融交易的重大亏损也许就可以完全避免。
第二，用于业绩评估。在金融投资中，高收益总是伴随着高风险，交易员可能不惜冒巨大的风险去追逐巨额利润。公司出于稳健经营的需要，必须对交易员可能的过度投机行为进行限制。所以，有必要引入考虑风险因素的业绩评价指标。
第三，估算风险性资本（Risk－based capital）。以VaR来估算投资者面临市场风险时所需的适量资本，风险资本的要求是BIS对于金融监管的基本要求。下图说明适足的风险性资本与 VaR值之间的关系，其中VaR值被视为投资者所面临的最大可接受（可承担）的损失金额，若发生时须以自有资本来支付，防止公司发生无法支付的情况。
从Yahoo获取数据
histPlot(SMI, main = "SMI Returns")
模型估计
SMI收益的数据有5078个观测值。我使用前3078个观察值对GARCH模型进行初始估计。其余的2000个观测值用于验证和测试。
library(rugarch)
library(zoo)
SMIdf <- as.data.frame(SMI)
#GARCH
#GARCH定义 (改变分布类型)
gspec11 <- ugarchspec(variance.model = list(model = "sGARCH",
garchOrder = c(1, 1)),
mean.model=list(armaOrder=c(0,0),
include.mean = FALSE),
distribution="norm")
结果
#VaR 结果
plot(Returns, type = "l", pch = 16, cex = 0.8, col = gray(0.2, 0.5),
ylab = "Returns", main = "95% VaR Forecasting", xaxt = "n")
从图中我们可以看到，VaR-GARCH（黑线）组合更加符合实际，降低了发生波动时的VAR限制，而对于静态VaR（红线），我们观察到了收益率连续突破界限。
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
R语言VAR模型的多行业关联与溢出效应可视化分析
【视频讲解】Python用LSTM长短期记忆网络GARCH对SPX指数金融时间序列波动率滚动预测
R 语言GJR-GARCH、GARCH-t、GARCH-ged分析金融时间序列数据波动性预测、检验、可视化
