最近我们被客户要求撰写关于LASSO回归的研究报告。
本文使用模拟数据比较了标准最小二乘法和lasso回归。
可下载资源
模拟假数据集
set.seed(0820)
n <- 50
p <- 25
beta <- rep(0,p)
beta[1:5] <- 1:5/5
X <- matrix(rnorm(n*p),n,p)
X <- scale(X)
Xb <- X%*%beta
Y <- X%*%beta+rnorm(n)
Y <- Y-mean(Y)
plot(cor(X,Y),xlab="j",ylab="Cor(Y,X_j)",main="Sample correlations",cex=2)绘制样本相关系数图
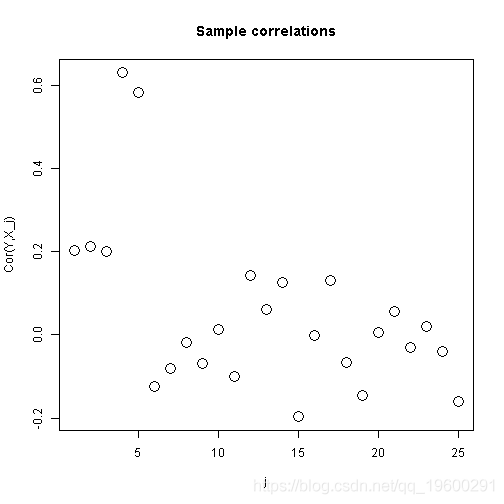
标准最小二乘法
summary(ols)##
## Call:
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.54540 -0.38971 -0.00738 0.49058 1.90900
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.914e-16 1.648e-01 0.000 1.00000
## X1 6.020e-01 2.097e-01 2.871 0.00841 **
## X2 5.924e-01 2.013e-01 2.944 0.00709 **
## X3 -1.106e-01 2.290e-01 -0.483 0.63363
## X4 1.117e+00 2.058e-01 5.427 1.42e-05 ***
## X5 1.234e+00 2.190e-01 5.633 8.46e-06 ***
## X6 -3.225e-01 2.322e-01 -1.389 0.17755
## X7 -1.954e-01 2.150e-01 -0.909 0.37231
## X8 1.466e-01 2.532e-01 0.579 0.56803
## X9 4.678e-02 2.353e-01 0.199 0.84409
## X10 -2.779e-01 2.151e-01 -1.292 0.20864
## X11 -7.308e-02 2.553e-01 -0.286 0.77717
## X12 -4.424e-02 2.642e-01 -0.167 0.86839
## X13 -1.078e-01 2.101e-01 -0.513 0.61270
## X14 3.000e-01 2.263e-01 1.326 0.19743
## X15 2.396e-01 2.480e-01 0.966 0.34365
## X16 -1.178e-01 2.285e-01 -0.515 0.61100
## X17 -2.409e-01 2.280e-01 -1.057 0.30104
## X18 -3.191e-01 2.396e-01 -1.332 0.19551
## X19 -1.207e-01 2.372e-01 -0.509 0.61553
## X20 1.721e-01 2.179e-01 0.790 0.43733
## X21 -1.677e-02 2.144e-01 -0.078 0.93831
## X22 3.706e-02 2.145e-01 0.173 0.86426
## X23 3.233e-02 2.108e-01 0.153 0.87938
## X24 -1.541e-01 2.343e-01 -0.658 0.51691
## X25 -1.970e-01 1.965e-01 -1.002 0.32622
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.166 on 24 degrees of freedom
## Multiple R-squared: 0.8416, Adjusted R-squared: 0.6767
## F-statistic: 5.102 on 25 and 24 DF, p-value: 7.861e-05
LASSO
plot(lasso)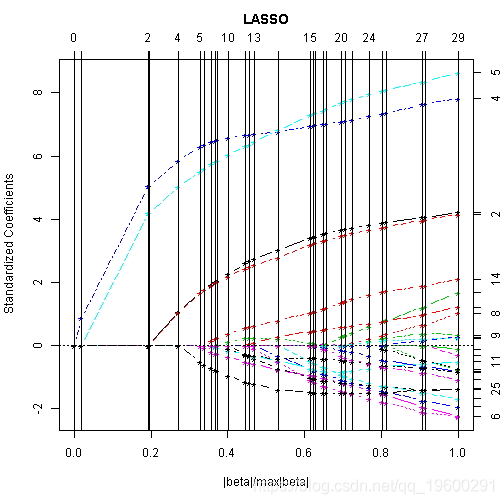
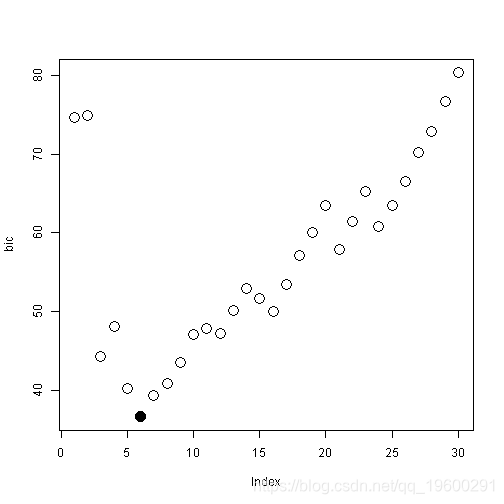
使用BIC选择路径上的最佳点
## df MSE bic
## Intercept 1 4.1174138 74.67329
## 2 3.8224639 74.86881
## 3 1.9171062 44.27691
## 4 1.9136899 48.09976
## 5 1.5118875 40.22806
## 6 1.3016560 36.65400
## 7 1.2693779 39.31051
## 8 1.2124870 40.92986
## 9 1.1814011 43.54326
## 10 1.1728179 47.09070
## 11 1.1016346 47.87201
## 12 1.0050559 47.19643
## 13 0.9867377 50.18875
## 14 0.9636054 52.91465
## 15 0.8686856 51.64164
## 16 0.7777734 50.02637
## 17 0.7700763 53.44111
## 18 0.7663544 57.11089
## 19 0.7510361 60.01336
## 20 0.7451598 63.53263
## 19 0.7196873 57.88151
## 20 0.7149486 61.46323
## 21 0.7141592 65.32002
## 20 0.7051259 60.77152
## 21 0.6875391 63.42065
## 22 0.6764241 66.51776
## 23 0.6739037 70.24313
## 24 0.6570954 72.89225
## 25 0.6564105 76.75213
## 26 0.6520870 80.33373
## [1] 0.2 0.4 0.6 0.8 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## [18] 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
# beta真值
round(beta_ols,3)
## X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
## 0.602 0.592 -0.111 1.117 1.234 -0.323 -0.195 0.147 0.047 -0.278
## X11 X12 X13 X14 X15 X16 X17 X18 X19 X20
## -0.073 -0.044 -0.108 0.300 0.240 -0.118 -0.241 -0.319 -0.121 0.172
## X21 X22 X23 X24 X25
## -0.017 0.037 0.032 -0.154 -0.197
# LASSO预测beta
round(beta_lasso,3)
## [1] 0.238 0.238 0.000 0.900 0.786 0.000 0.000 0.000 0.000 0.000
## [11] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
## [21] 0.000 0.000 0.000 0.000 -0.075
随时关注您喜欢的主题
#MSE - OLS
mean((beta-beta_ols)^2)
## [1] 0.06204978
#MSE - LASSO
mean((beta-beta_lasso)^2)
## [1] 0.01795647可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据：旅游市场差异、价格预测
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
