最近我们被客户要求撰写关于IDI，NRI指标的研究报告。
本文展示了R语言如何在生存分析与Cox回归中计算IDI，NRI指标 的例子。
可下载资源
读取样本数据
D=subset(pbc, select=c("time","status","age","albumin","edema","protime","bili"))
D$status=as.numeric(D$status==2)
D=D[!is.na(apply(D,1,mean)),] ; dim(D)在诊断试验中，我们比较两个模型的优劣时，除了可以比较两个模型ROC曲线下面积外，还可以用定量的指标来比较一个模型比另外一个模型诊断准确率改进的程度。NRI（Net Reclassification Improvement，重分类改善指标），NRI定量地表示一个指标在某界值下的诊断准确率比另一指标准确率提高多少，容易理解，也比较容易计算。缺点是只考虑了界值时的情况，同时另外一个指标可以弥补这个不足，即IDI。
IDI（Integrated Discrimination Improvement，综合判别改善指数）也是Pencina等人于2008年提出的，它使用模型（或指标）对每个个体的预测概率计算得到，计算方法为：
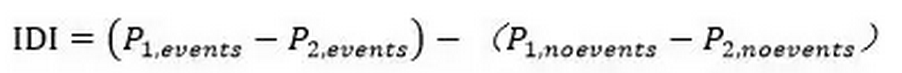
P1,events和P2,events为金标准阳性的所有研究对象在模型1和模型2中诊断为阳性的平均概率，P1,noevents和P2,noevents为金标准阴性的所有研究对象在模型1和模型2中诊断为阳性的平均概率。公式前半部分为金标准阳性（患者）中，计算每个个体的模型1的预测概率与模型2的预测概率之差，再计算所有差的平均数，此平均值越大，认为模型1较好；公式后半部分为金标准阴性（非患者）中，计算每个个体的模型1的预测概率与模型2的预测概率之差，再计算所有差的平均数，此平均值越小，认为模型1较好；因此总体来说，IDI越大，认为模型1越好。IDI的检验思想与AUC类似，分别考虑了不同界值下指标的整体情况，可以代表指标（模型）的整体改善情况。
NRI和IDI的应用定量地解决了两个模型诊断效能比较的问题，可以定量评价一个指标比另外一个指标诊断效能改善情况。NRI和IDI两个指标可以形象地展示研究对象被正确重新分类（判别）的比例，易于理解，也逐渐被研究者接受。在卫生经济学评价中两个指标的应用价值更高，NRI和IDI可以比较容易计算成本效益，是传统指标不具备的功能，预计将会广泛用于卫生经济学研究中。
参考文献
[1] Pencina M J, D’Agostino R S, D’Agostino RJ, et al. Evaluating the added predictive ability of a new marker: from areaunder the ROC curve to reclassificationand beyond.
[2] Kerr K F, Mcclelland R L, Brown E R, etal. Evaluating the incremental value of new biomarkers with integrateddiscrimination improvement.
## [1] 416 7查询部分数据（结果和预测因子）
head(D)
## time status age albumin edema protime bili
## 1 400 1 58.76523 2.60 1.0 12.2 14.5
## 2 4500 0 56.44627 4.14 0.0 10.6 1.1
## 3 1012 1 70.07255 3.48 0.5 12.0 1.4
## 4 1925 1 54.74059 2.54 0.5 10.3 1.8
## 5 1504 0 38.10541 3.53 0.0 10.9 3.4
## 6 2503 1 66.25873 3.98 0.0 11.0 0.8模型0和模型1的结果数据和预测变量集
outcome=D[,c(1,2)]
covs1<-as.matrix(D[,c(-1,-2)])
covs0<-as.matrix(D[,c(-1,-2, -7)])
head(outcome)## time status
## 1 400 1
## 2 4500 0
## 3 1012 1
## 4 1925 1
## 5 1504 0
## 6 2503 1head(covs0)
## age albumin edema protime
## 1 58.76523 2.60 1.0 12.2
## 2 56.44627 4.14 0.0 10.6
## 3 70.07255 3.48 0.5 12.0
## 4 54.74059 2.54 0.5 10.3
## 5 38.10541 3.53 0.0 10.9
## 6 66.25873 3.98 0.0 11.0head(covs1)
## age albumin edema protime bili
## 1 58.76523 2.60 1.0 12.2 14.5
## 2 56.44627 4.14 0.0 10.6 1.1
## 3 70.07255 3.48 0.5 12.0 1.4
## 4 54.74059 2.54 0.5 10.3 1.8
## 5 38.10541 3.53 0.0 10.9 3.4
## 6 66.25873 3.98 0.0 11.0 0.8推理
t0 = 365 *5
x<-<IDI.INF(outcome, covs0, covs1, t0, npert=200) ;输出
## Est. Lower Upper p-value
## M1 0.090 0.052 0.119 0
## M2 0.457 0.340 0.566 0
## M3 0.041 0.025 0.062 0M1表示IDI
M2表示NRI
M3表示中位数差异
图形演示
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
多状态马尔可夫链、生存分析心脏同种异体移植血管病变（CAV）数据可视化|附数据代码
【专题】人工智能行业C_Suite全球AI指标报告报告合集PDF分享（附原数据表）
R语言PLS-DA模型分析不同中医组别患者间差异指标数据可视化
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
