本研究以太阳黑子活动数据为研究对象，旨在帮助客户探索其未来走势并提供预测分析。
首先，通过对数据的清洗和处理，包括离群值的识别与处理以及时间序列的建立，确保了数据的质量和可靠性。
根据发电机模型，研究太阳黑子的规律并揭示了太阳黑子活动数据的特征，太阳的功率谱密度大概为0.09，具有周期性规律具有11年周期规律，再通过季节性分解出真正的趋势和残差。
建立SARIMA模型和LSTM模型，通过单位根得到差分一次数据就较为平缓，通过相关参数进行了数据拟合，利用残差序列进行LSTM模型拟合。
通过可视化手段展示了预测结果，并结合常见的评价指标如均方根误差和平均绝对误差等对预测性能进行了评估和分析。最终判断SARIMA模型与LSTM模型的融合模型超过SARIMA模型和LSTM模型。
SARIMA-LSTM融合模型相对于单个模型有什么优势和劣势？
智能体：
SARIMA-LSTM融合模型相较于单个模型具有显著的优势。首先，SARIMA模型擅长捕捉时间序列中的线性趋势和季节性特征，而LSTM模型则能够有效处理非线性关系和长期依赖性。通过将两者结合，融合模型能够同时利用SARIMA的线性预测能力和LSTM的非线性处理能力，从而提高预测的准确性和稳定性。例如，在太阳黑子数量预测中，融合模型的均方根误差（RMSE）和平均绝对误差（MAE）均低于单独的SARIMA和LSTM模型，表明其在预测精度上更具优势。
然而，融合模型也存在一些劣势。其复杂性增加，导致训练时间可能较长，并且在模型调参过程中需要同时优化两个模型的参数，增加了调参的难度。此外，融合模型的解释性相对较弱，不如单一模型直观。因此，在选择使用融合模型时，需权衡其优势与劣势。
研究背景与意义
在 2024 年元旦当日，太阳竟然爆发了 X5.0 级强耀斑，进而导致太平洋、大洋洲以及南美多地的短波通信中断将近 1 小时。而此事件恰好在太阳黑子数量峰年的附近，国家空间天气监测预警中心表明，当前太阳活动正处于第 25 周峰值的区间（预计在 2024 – 2025 年达到峰值）。而太阳黑子，它作为太阳活动的核心标志，其数量是直接能反映太阳活跃程度以及耀斑爆发概率的。
黑子数量持续攀升，预示着太阳活动进入高发阶段。太阳活动引发的空间天气事件对航天、导航、通信等领域构成威胁，其辐射可干扰高频通信系统，甚至影响地基技术设备可靠性。
太阳黑子不仅是太阳磁场活动的集中体现，更是预测太阳活动趋势的关键指标。通过研究黑子数的准周期变化，可预判太阳活动周期整体态势，进而为空间天气预警、电离层监测及短波通信保障提供科学依据。随着地球通信系统向高频段升级，太阳活动对技术系统的影响愈发显著。太阳黑子数量预测具有双重价值：既深化对恒星活动规律的认识，又为应对空间环境挑战提供技术支撑[1]。
作者
Kaizong Ye
可下载资源
国内外研究现状
几十年来，研究人员一直在试图预报太阳黑子的出现，并且试图在黑子出现之前能在太阳内部探测到其上浮的过程，从而为更好地预测空间天气服务。
2011年，中美科学家团队在《科学》杂志发表突破性研究成果，首次揭示太阳黑子形成前的深层磁场活动规律。赵俊伟博士团队通过局部日震学方法分析卫星观测数据，发现大型太阳黑子浮现前约两天，太阳内部6万公里深处即出现磁场浮现现象，该磁场以声波形式传播并导致p型声波加速约十秒。进一步研究表明，磁场浮现速度在初始探测后一两天内显著加快，最终形成可见黑子。这项基于SOHO（太阳和日光层观测卫星）/MDI（米歇尔森多普勒成像仪）和SDO（太阳动力学天文台）/HMI（日光磁成像仪）数据的创新研究，不仅建立了太阳活动区浮现的预测方法，为空间天气预报提供关键依据，更深化了对太阳磁场生成机制与黑子形成过程的理解，标志着太阳物理研究的重要进展。随着时间的推移，后面的研究人员深入研究了相关数据[2]。
想了解更多关于模型定制、咨询辅导的信息？
数据收集
太阳黑子的数据收集是太阳物理研究的重要组成部分，比利时皇家天文台（Royal Observatory of Belgium）是进行太阳黑子观测和数据收集的机构之一。它们公布的国际太阳黑子数据，为科学家们提供了宝贵的研究资源。
本文获取了如下原始数据，该原始数据可以保证准确性、真实性，用于后续模型训练和预测。原始数据如表3-1所示：
表3-1 原始数据表（数据来源：比利时皇家天文台’SN_y_tot_V2.0.txt’）
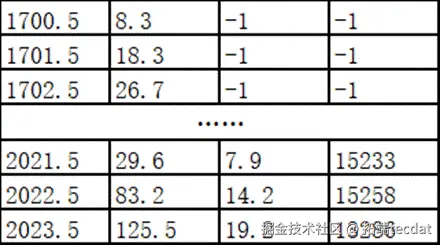
在获取数据上，本文读取’SN_y_tot_V2.0.txt’文件，获得5个列，分别是’Year’，‘Mean_total_sunspot_number’，‘Mean_standard_deviation’，‘Observations’，‘Indicator’。
视频
【视频讲解】Python用LSTM、Wavenet神经网络、LightGBM预测股价
视频
【讲解】ARIMA、XGBOOST、PROPHET和LSTM预测比特币价格
视频
【视频讲解】Python深度学习股价预测、量化交易策略：LSTM、GRU深度门控循环神经网络附代码数据
代码如下：
数据清洗
本文需要进行数据审查、缺失值处理、异常值处理以及平稳性处理。从而确保数据的有效性。本文选择将值为 -1 （表示没有可用的数字），和“*”符号表示的临时数据（表示年平均值仍包含临时每日值，天文台后续将会修订）剔除，防止这些数据使模型性能下降。
数据审查
数据审查，全面扫描数据集以发现缺失值、异常值、逻辑矛盾及重复记录等问题。为了扫描数据集，使用head函数进行观察数据前五行，再绘制原始年平均太阳黑子数量图以便观察。根据以上要求构建代码如下：
原始年平均太阳黑子数量图如下：
图3-1 原始年平均太阳黑子数量图
通过观察原始年平均太阳黑子数量，可以发现它带有明显的周期性，所以本文选择在后文通过高级频域分析工具根据发电机模型进行探索周期性。
异常值检测
本文选择对异常数据进行处理，由于“*”符号表示年平均值仍包含临时的每日数值，并后续会被天文台修订，所以剔除。对太阳黑子数的年平均标准差为-1和年平均太阳黑子总数的观测次数为-1的无效数据进行剔除。代码如下：
异常值的出现是测量误差、或者真实的、非典型的太阳活动事件造成的。因为异常值会对预测模型的准确性产生显著影响，所以使用离群值替换，提高模型的性能。运行代码得到下图3-2：
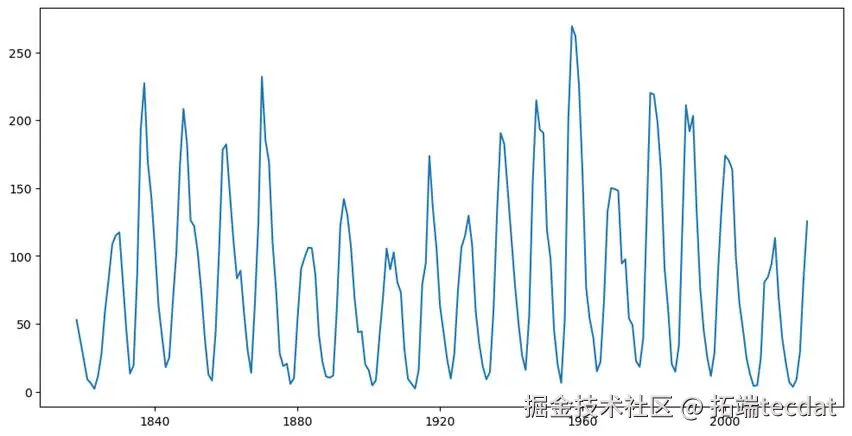
图3-2：异常值处理后的图像
平稳性处理
因为SARIMA模型要求数据是平稳的，即均值和方差是常数，所以如果太阳黑子数量序列不是平稳的，那么需要进行多次差分运算，直到得到的序列足够平稳。设Z为差分后的序列，差分运算为：
| (10) |
|---|
这里∆表示差分操作，反复应用差分运算，直到 Z 达到平稳性。
本文将数据转换为时间序列，进行三次差分得到判断为时间序列是平稳的。本文对数据进行了三次差分以此来检验是否是单位根，代码如下：
运行代码得到下表3-5 ADF检验表：
随时关注您喜欢的主题
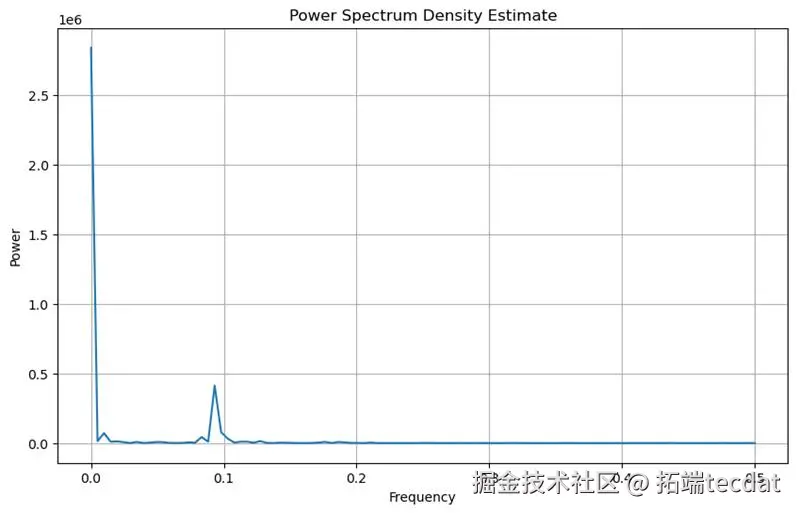
傅里叶变换
由于本节探索太阳黑子的周期性，所以本文选择了傅里叶变换。傅里叶变换是时间序列分析中常常使用到的一种方法，傅里叶变换将信号分解为不同频率的正弦波和余弦波的叠加，傅里叶变换通过频域分解，将周期性信号的能量集中到特定频率点，形成清晰可辨的谱峰，通过这个原理绘制频谱图。
图3-3 频谱图
主要周期的倒数即为太阳黑子数量的周期性变化，可得出太阳黑子数量序列具有11年的周期性变化。
因为时间序列数据带有明显的周期性，所以本文选择SARIMA模型最为基础模型，SARIMA模型的参数选择导致了线性预测值的精准性。
SARIMA模型
本文考虑共七个参数：p是自回归项，d是差分次数，q是移动平均项；大写的P、D、Q是对应的季节性部分参数；季节周期s取决于数据的时间间隔[12]。首先需要考虑数据是否平稳，所以需要进行单位根检测。其次需要观察ACF、PACF以及SACF与SPACF图观察获得其余参数。
通过代码绘制图4-3：自相关图（ACF）和非自相关图（PACF）图：
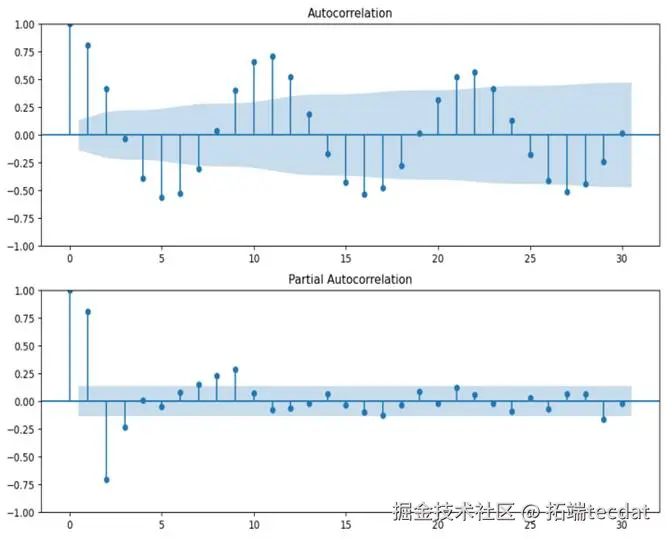
图4-3 自相关图（ACF）和非自相关图（PACF）图
观察上图可以发现，ACF在lag=1后突然截尾，可以判断q=1。PACF在lag=2后截尾，可以判断p=2。这为模型定阶提供了重要依据。
SARIMA模型的实现
通过上面步骤从而确定了七个参数，导入模型数据完成模型的实现。
LSTM神经网络
LSTM模型能够更好的处理非线性序列，所以本研究选择LSTM神经网络作为基模型[13]。通过处理残差序列得到非线性预测值，与上文的SARIMA模型线性预测值进行加和，从而得到融合模型预测值。
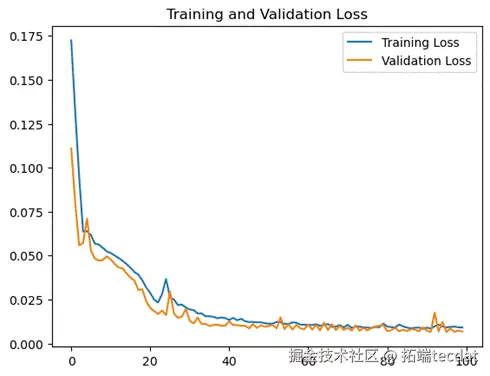
图4-6 LSTM损失函数
通过上图的发现两条曲线都从左上角开始下降，这意味着在训练的初期，模型的损失值较高，性能较差。之后，两条曲线都开始下降，并趋近于0点，这表明模型正在逐渐收敛，性能在不断提高。当损失值稳定在一个较低水平时，可以认为模型已经收敛并达到了最佳性能。从图中可以看出，训练损失和验证损失的曲线走势大致相同，这表明模型在训练集和验证集上的性能表现是一致的，说明模型没有出现过拟合或欠拟合的情况。根据学习曲线本研究可以将训练次数设定为40次，此时损失值稳定在一个较低水平同时保证了训练时间短。
融合模型的设计
融合模型是通过结合多个基模型预测结果来提升整体预测性能的机器学习范式，在本研究中，基模型为SARIMA模型与LSTM模型，它们分别具备良好的处理数据中线性和季节性成分的性能与处理非线性或复杂成分的性能，在众多方向发展已经有研究。图4-7融合模型示意图[14]。
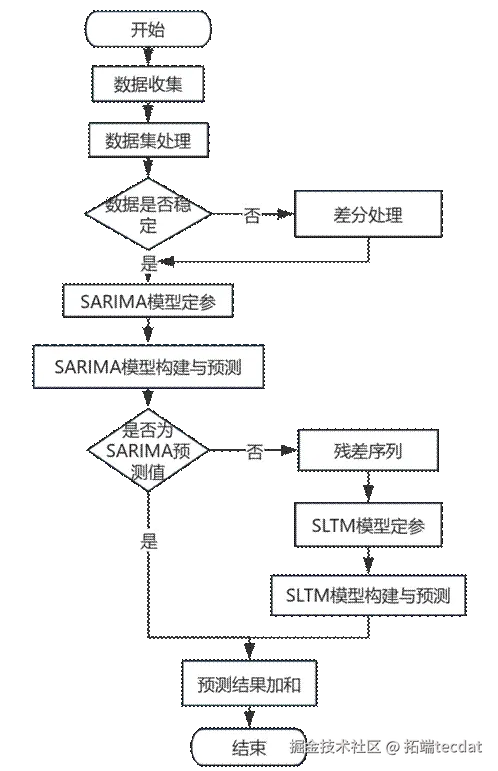
图4-7 融合模型流程图
该流程图系统描述了太阳黑子数量序列的预测分析流程：首先进行数据稳定性检验，若序列非平稳，进行多次差分直到序列平稳，SARIMA侧重捕捉周期性特征，于是提取季节性与趋势数据对SARIMA进行参数优化与模型构建，得到SARIMA模型结果，与真实值的差值为残差序列。SLTM补充局部趋势分析，于是通过残差序列对SLTM模型进行参数优化与模型构建。最后将两模型的预测结果进行加和整合，平衡季节性与非线性动态特征，从而提升太阳黑子数量预测的鲁棒性与准确性。
可视化与模型比较
可视化，可以让读者高效地获取和理解数据，从而更快地做出决策。同时，可视化降低数据的复杂性和抽象性，能够轻松地访问和理解数据，从而更准确地做出决策。模型比较更容易展示模型的性能，体现融合模型的优势。
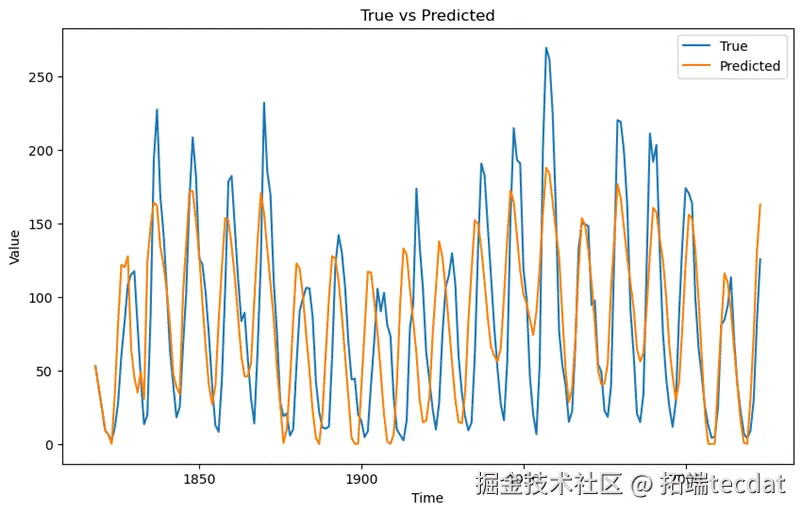
图5-1 SARIMA模型的预测值与实际值对比
就图中而言，蓝色的实际曲线以及橙色的预测曲线，皆显现出明显的以 11 年为周期的波动特征（太阳活动周期），由此表明 SARIMA 模型成功将太阳黑子活动的周期性规律予以捕捉。值得一提的是，在 1830 – 1910 年这一期间，预测曲线与实际曲线的波峰波谷位置达成了高度的吻合。并且，预测曲线能够较为良好地跟随着实际数据的长期趋势，在 1870 – 1970 年的上升期以及 1970 – 2010 年的下降期中，该模型都可以有效地对整体变化趋势进行追踪。然而，在部分周期当中（在 1890 – 1930 年期间），预测曲线的波峰/波谷的出现时间相较于实际曲线滞后了大约 1 – 2 年，这意味着模型对于周期转换的敏感度存在不足。
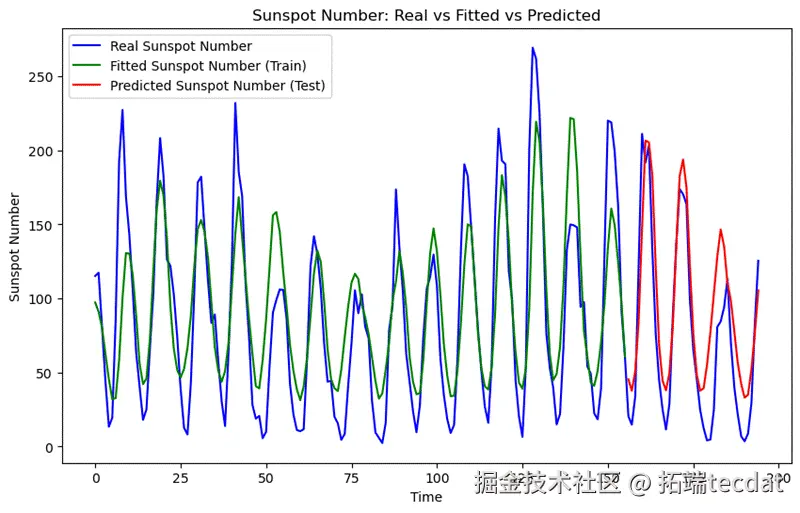
图5-2 LSTM模型的预测值与实际值对比
本文为了增强LSTM神经网络模型的泛化性能并有效规避过拟合风险，将残差序列按8:2的比例划分为训练子集和测试子集。在模型构建阶段，本文仅利用训练子集进行，获得绿色拟合曲线；在模型验证阶段，则完全基于测试子集，获得红色预测曲线。图中绿色拟合曲线与蓝色实际曲线在训练区间几乎重合，表明LSTM模型具备强大的非线性映射能力，能精准捕捉太阳黑子数复杂的变化模式；红色预测曲线中呈现以下特征，预测波峰高度比实际值低约30%，波谷深度浅约15%。
图5-3 融合模型对太阳黑子的未来十年预测
通过上图，本文发现，预测曲线（绿色）与实测数据（蓝色）在波动形态上高度吻合，表明模型成功捕捉到了太阳活动约11年的周期，峰值可能出现在2025年前后，模型可以捕捉到太阳活动从活跃期向弱活动期的过渡特征。
模型比较
在模型比较中常常使用RMSE、MAE、R² Score、MAPE和RMSE指标来综合评价模型效果[15]。通过计算不同模型的性能指标，将数据进行汇总得到下表5-1不同模型的不同指标评价表：
表不同模型的不同指标评价表
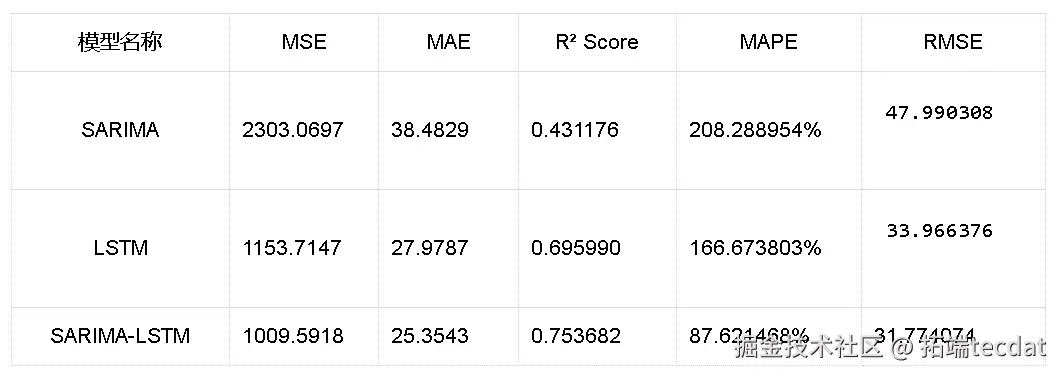
SARIMA模型的MSE为2303.0697，LSTM模型为1153.7147，而融合模型仅为1009.0631，这意味着融合模型的预测值与实际值之间的差异最小，其预测准确性高于其它两个模型。
SARIMA模型的MAE为38.4829，LSTM模型为27.9787，而融合模型则为25.3542，这意味着融合模型的预测值与实际值之间的平均绝对误差最小，其预测准确性远高于其它两个模型。
SARIMA模型的R² Score为0.431176，LSTM模型为0.695990，而融合模型高达0.753682，这表明融合模型能够更好地解释数据中的变动，其预测能力更强。
SARIMA模型的MAPE高达208.288954%。LSTM模型的MAPE为166.673803%，而融合模型仅为87.621468%。这进一步证实了融合模型在预测准确性上的优势。
SARIMA模型的RMSE为47.990308，LSTM模型为33.966376，而融合模型为31.774074，融合模型的RMSE远低于其它两个模型，其预测的准确性远高于其它两个模型。
指标雷达图：
图5-4 指标雷达图
综上所述，融合模型的预测值与实际值之间的差异最小，其预测准确性远高于其它两个模型，能够更好地解释数据中的变动，其预测能力更强。
结束语
本文针对太阳黑子数量的物理原理，使用傅里叶变换和功率谱密度估计：傅里叶变换用于将时域信号转换到频域，功率谱密度（PSD）估计提供了信号在频率域上的能量分布。得到太阳周期系数为11年，捕捉到时间序列数据季节性。本文将SARIMA模型与LSTM神经网络进行融合。融合模型具有SARIMA模型的时间序列预测的能力，适用于具有明显季节性的太阳黑子数量序列数据；同时具有LSTM模型解决长期依赖问题的性能，也适用于经过SARIMA模型处理后的太阳黑子数量序列的数据，从而大大提高了模型的各项指标，更好的预测太阳黑子的数量。
- 乐贵明.日地空间天气强关联事件[M].北京市：气象出版社:202006.93.
- 邓元勇, 周桂萍, 代树武, 等. 太阳极轨天文台[J]. 科学通报, 2023, 68(4): 298-308.
- 方巍.Python数据挖掘与机器学习实战[M].北京市：机械工业出版社:202303.593.
- 安小米.大数据治理前沿[M].北京市：中国人民大学出版社:202310.285.
- 汪静,郑婷婷.Python数据预处理[M].北京市：人民邮电出版社:202303.189.
- 李富羽. 新黑子数的活动周特征分析[D]:[博士论文]. 中国科学院大学,2019.
- 郭佳俊.季节性时间序列调整与预测研究[D]:[硕士论文].陕西省：西北农林科技大学,2023.
关于分析师
在此对Peng Fan对本文所作的贡献表示诚挚感谢，他完成了数据科学与大数据技术专业的学位，专注深度学习、数理金融领域。擅长Python 。
每日分享最新报告和数据资料至会员群
关于会员群
- 会员群主要以数据研究、报告分享、数据工具讨论为主；
- 加入后免费阅读、下载相关数据内容，并同步海内外优质数据文档；
- 老用户可九折续费。
- 提供报告PDF代找服务
非常感谢您阅读本文，如需帮助请联系我们！
Python+AI提示词用LSTM和注意力机制的苹果公司股票价格预测
Python、R语言南方电网、电力负荷数据多模型构建：分位数回归、GAM样条曲线、指数平滑和SARIMA与预测实践
【视频】文本挖掘专题：Python、R用LSTM情感语义分析实例合集|上市银行年报、微博评论、红楼梦数据、汽车口碑数据采集词云可视化
