像任何统计建模一样,贝叶斯建模可能需要为你的研究问题设计合适的模型,然后开发该模型,使其符合你的数据假设并运行。

最近我们被客户要求撰写关于贝叶斯线性回归的研究报告。统计模型可以在R或其他统计语言的各种包中进行拟合。但有时你在概念上可以设计的完美模型,在限制了你可以使用的分布和复杂性的软件包或程序中很难或不可能实现。这时你可能想转而使用统计编程语言,如Stan。
可下载资源
1. 了解 Stan
Stan是一种新式的语言,它提供了一种更全面的学习和实现贝叶斯模型的方法,可以适应复杂的数据结构。Stan开发团队的一个目标是通过清晰的语法、更好的采样器(这里的采样是指从贝叶斯后验分布中抽取样本)以及与许多平台(包括R、RStudio、ggplot2和Shiny)的集成,使贝叶斯建模更易于使用。
-
用训练数据得到似然函数likelihood,再加上一个先验分布prior,得到一个后验分布posterior.
-
对于一个新的测试数据x,用之前得到的posterior作为权重在整个参数空间里计算一个加权积分,得到一个预测分布。
在实际中,除了少数情况(比如先验和似然函数都是高斯分布),那个后验分布的形式一般都很复杂,第二步里的积分是积不出来的。这时候就要采取一些近似方法,近似方法又分为两大类:
-
简化复杂的后验分布,然后就能算出积分的解析形式了。具体方法有变分推断,Laplace近似等。这类方法的特点是人算起来困难,机器跑起来快。
-
用采样的方法搞定后验分布。具体方法有Gibbs采样,HMC采样等。这类方法反过来了,人算起来简单,但是机器跑起来慢。
-
采样方法还有一个好处,就是精度算得高~
在这个入门教程中,我们将从一个线性模型开始,经历模型建立的迭代过程。在我们的高级stan教程中,我们将探索更复杂的模型结构。
首先,在建立模型之前,你需要定义你的问题并了解你的数据。探索它们,绘制它们,计算一些汇总统计。
一旦你对你的数据和你想用统计模型回答的问题有了了解,你就可以开始建立贝叶斯模型的迭代过程。
- 设计你的模型。
- 选择先验
- 对后验分布进行采样。
- 检查模型收敛(traceplots、rhats )
- 使用后验预测批判性地评估模型并检查它们与您的数据的比较情况
- 重复…
模拟数据也是很好的做法,以确保你的模型正确,作为测试你的模型的另一种方式。
2. 数据
首先,让我们找到一个可以拟合简单线性模型的数据集。 气候变化对地球最显着的影响之一是北半球每年海冰范围的减少。让我们使用 Stan 的线性模型探索海冰范围如何随时间变化。
通过运行setwd("your-file-path") 包含您自己的文件路径的代码 ,将您的工作目录设置为您保存数据的文件夹 。现在,让我们加载数据:
# 添加stringsAsFactors = F意味着数字变量将不会被
# 作为因子/分类变量读入
ece <- red.cv("sv", stinsAsFators = F)
我们来看一下数据:
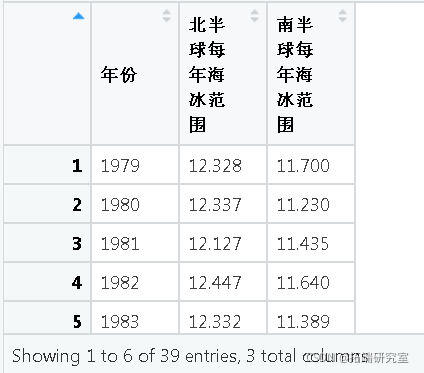
我们可以用这些数据提出什么研究问题?以下情况如何:
研究问题: 北半球的海冰范围是否会随着时间的推移而减少?
为了探索这个问题的答案,首先我们可以做一个数字。
plot( th ~ yr, data)
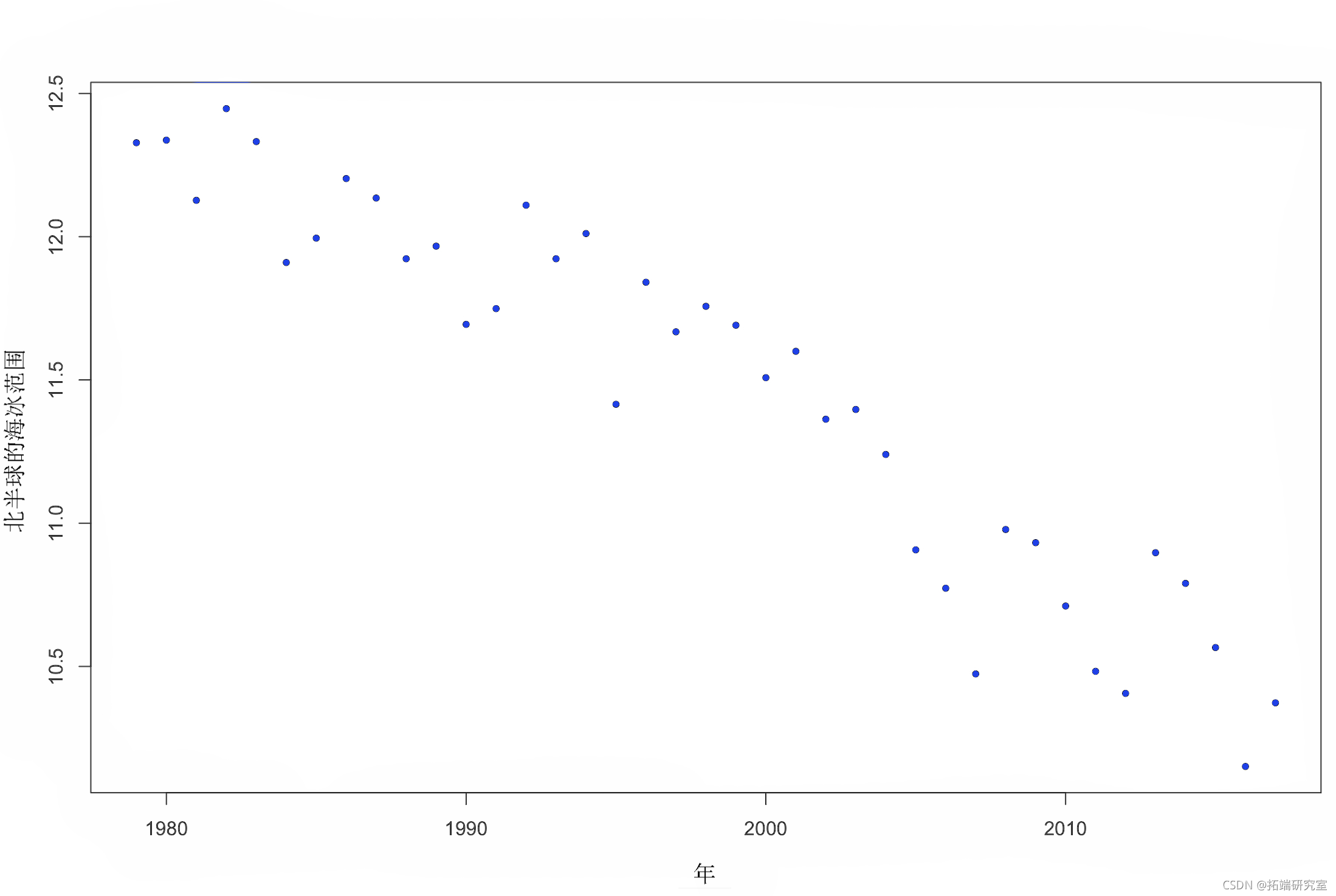 图 1. 北半球海冰范围随时间的变化。
图 1. 北半球海冰范围随时间的变化。
现在,让我们使用 lm().
l1 <- lm(exnoh ~ yer, data = sie) summary(l1)
我们可以将该模型添加到我们的绘图中:
ablne(m1, l = 2, ty = 2, w = 3)
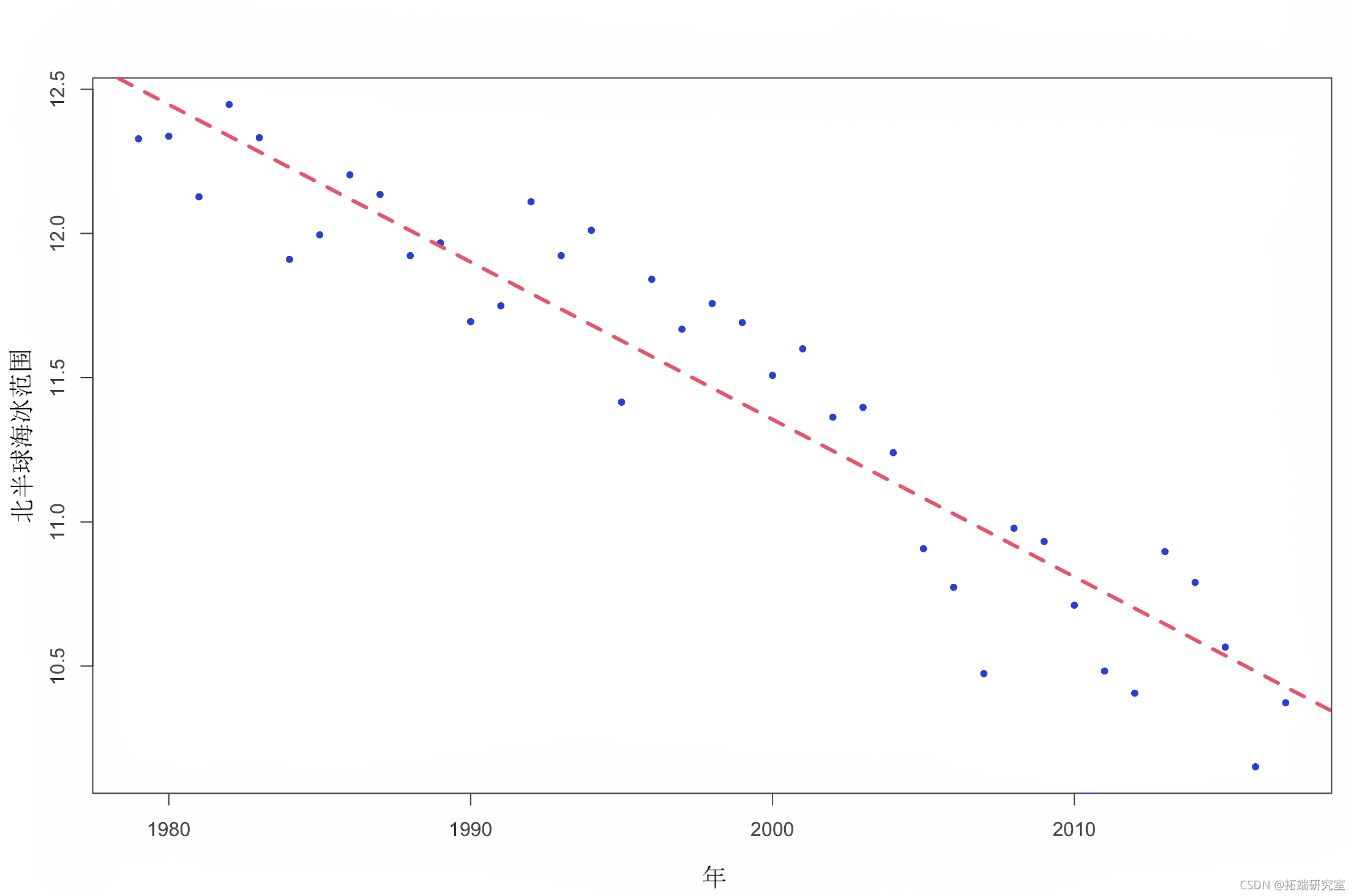 图 2. 北半球海冰范围随时间的变化(加上线性模型拟合)。
图 2. 北半球海冰范围随时间的变化(加上线性模型拟合)。
记住线性模型的方程:
y = α + β ∗ x + 误差
在 Stan 你需要指定你想模型。
也许我们已经找到了问题的答案,但本教程的重点是探索使用编程语言 Stan,所以现在让我们尝试在 Stan 中编写相同的模型。
准备数据
让我们重命名变量并将年份从 1 索引到 39。关于贝叶斯模型的一个关键是您必须使用信息分布来描述数据中的变化。因此,您希望确保您的数据符合这些分布,并且它们将适用于您的模型。在这种情况下,我们真的想知道从数据集的开始到数据集结束的海冰是否发生了变化,而不是 1979 年到 2017 年。我们不需要我们的模型估计 500 年或 600 年的海冰是什么样的,就在我们的数据集的持续时间内。因此,我们将年份数据设置为索引 1 到 30 年。
x <- I(year - 1978)
我们可以使用新数据重新运行该线性模型。
summary(lm1)
我们还可以从我们的简单模型中提取一些关键的汇总统计数据,以便我们Stan 稍后可以将它们与模型的输出进行比较 。
coeff\[1\] # 截距值 coeff\[2\] # 斜率 sigma(lm1) # 残差
现在让我们将其转换为用于输入Stan 模型的数据框 。传递给 Stan 的数据需要是命名对象列表。此处给出的名称需要与模型中使用的变量名称相匹配。
库
–
请确保安装了以下库(这些是本Stan 教程和下一个教程的库 )。 rstan 是最重要的,如果您没有 C++ 编译器,则需要一些额外的东西。
3. Stan 程序
我们将首先用语言编写一个线性模型 Stan。这可以写在你的 R 脚本中,或者单独保存为一个 .stan 文件并调用到 R.
一个 Stan 程序具有三个必需的“块”:
- “数据” 块:您可以在其中声明数据类型、它们的维度、任何限制(即 upper = 或 lower = ,用作检查
Stan)及其名称。 - “参数” 块:您可以在此处指明要建模的参数和名称。对于线性回归,我们希望对回归线周围的误差的截距、任何斜率和标准偏差进行建模。
- “模型” 块:这是包含任何抽样语句的地方,包括正在使用的模型。模型块是指明要为参数包含的任何先验分布的地方。如果未定义
Stan先验,则 使用默认先验uniform(-infinity, +infinity)。您可以在声明参数时使用上限或下限来限制先验(即lower = 0\> 确保参数为正)。
随时关注您喜欢的主题
采样由 ~ 符号表示,并且 Stan 已经包含许多常见的分布作为矢量化函数。
还有四个可选块:
- “功能”
- “转化的数据”
- “转换后的参数
- “生成的数量”
注释// 在 Stan中用 表示 。该write("model code", "file_name") 允许我们在 R 脚本中编写 Stan 模型并将文件输出到工作目录(或者您可以设置不同的文件路径)。
write("//简单线性回归的模型
数据
int < lower = 1 > N; // 样本大小
vector\[N\] x;// 预测
vecor\[N\] y;// 结果
参数
real alha; // 截距
real beta; // 斜率(回归系数)
real < loer = 0 > sima; // 误差SD
模型
y ~ nrmal(alpha + x * beta , siga);
产生的数量
// 后验预测分布" 。
"md1.stan"
首先,我们应该检查我们的 Stan 模型以确保我们编写了一个文件。
现在让我们保存该文件路径。
"model1.stan"
在这里,我们隐式地将 uniform(-infinity, +infinity) 先验用于我们的参数。
4. 运行Stan 模型
Stan 程序C++ 在被使用之前被遵守 。这意味着在 R 可以使用模型之前需要运行 C++ 代码。为此,您必须 C++ 安装编译器。编译后,您可以在每个会话中多次使用模型,但在开始新R 会话时必须重新编译 。有许多 C++ 编译器,而且它们在不同系统中通常是不同的。如果您的模型一堆错误,请不要担心。只要模型可以与该stan() 函数一起使用 ,它就可以正确编译。
如果我们想使用以前编写的 .stan 文件,我们在file 函数中使用 参数 stan_model() 。
我们通过使用stan() 函数拟合我们的模型 ,并为它提供模型、数据,并指示预热的迭代次数(这些迭代稍后不会用于后验分布,因为它们只是模型“预热” ”),总迭代次数,我们要运行的链数,我们要使用的内核数(Stan 为并行化而设置),它表示同时运行的链数(即,如果您的计算机有四个内核) ,您可以在每个链上运行一个链,同时创建四个链)和细化,这是我们想要存储我们的预热后迭代的频率。“thin = 1”将保留每次迭代,“thin = 2”将保留每一秒,依此类推……
Stan 如果warmup = 未指定参数,则自动使用一半的迭代作为预热 。
stan(fie =moel1, data = data, wrmup = 500, ier = 1000, chais = 4, cres = 2, thn = 1)
访问fit 对象的内容
结果 stan() 保存为 stanfit 对象(S4 类)。
我们可以通过执行对象的名称来获取参数估计和采样器诊断的汇总统计信息:
fit

您能看到指示您的 C++ 编译器已运行的文本吗?
从这个输出中,我们可以通过查看Rhat 每个参数的值来快速评估模型收敛性 。当这些值等于或接近 1 时,链已经收敛。还有许多其他诊断方法,但这对 Stan 来说很重要。
模型输出展示了什么?你怎么知道你的模型已经收敛了?
我们还可以通过从模型对象中提取参数来查看参数的完整后验。有很多方法可以查看后验。
poteir <- exrat(fit)
extract() 将每个参数的后验估计放入一个列表中。
让我们与我们之前使用“lm”的估计进行比较:
plot(y ~ x)
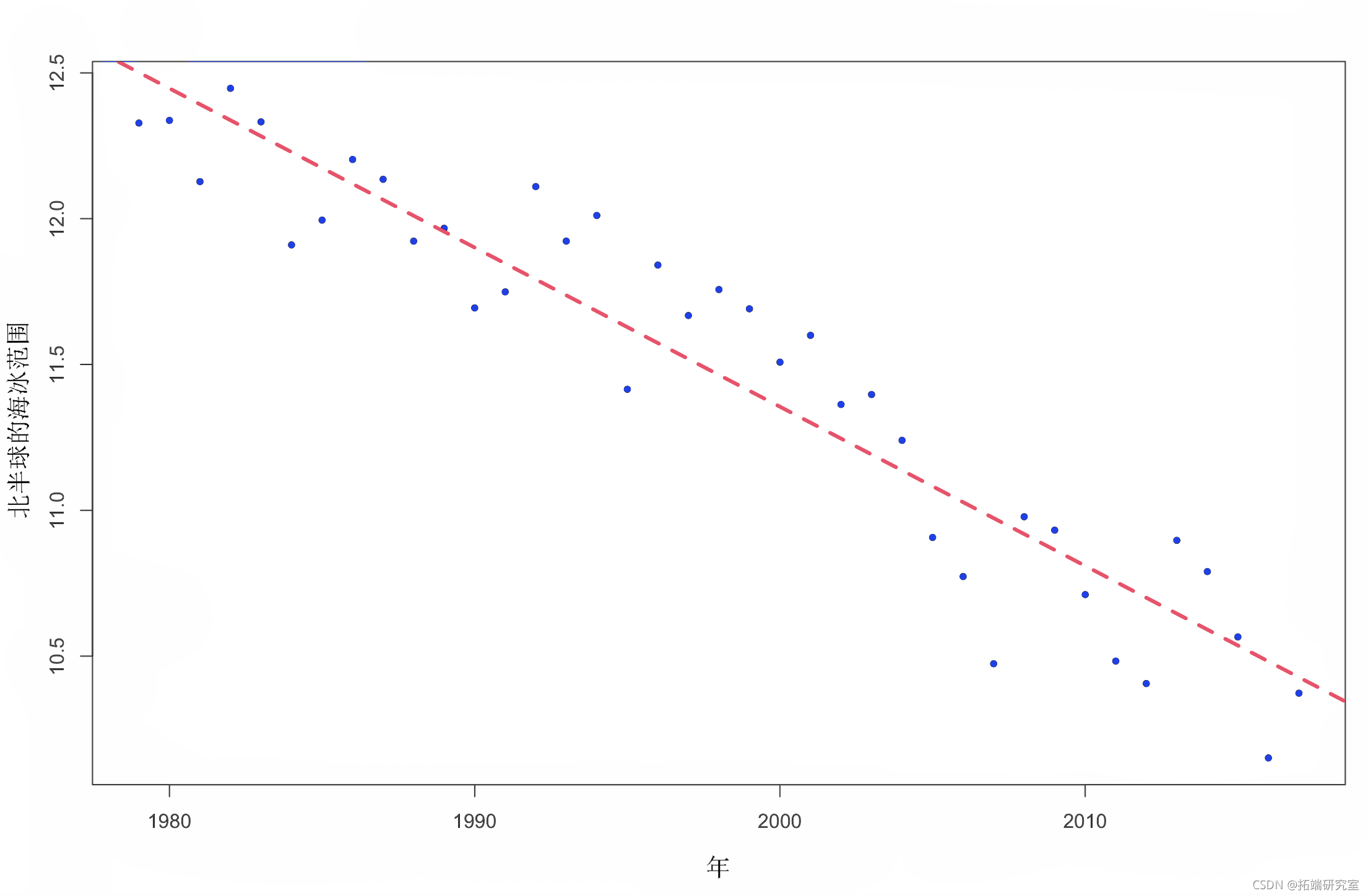
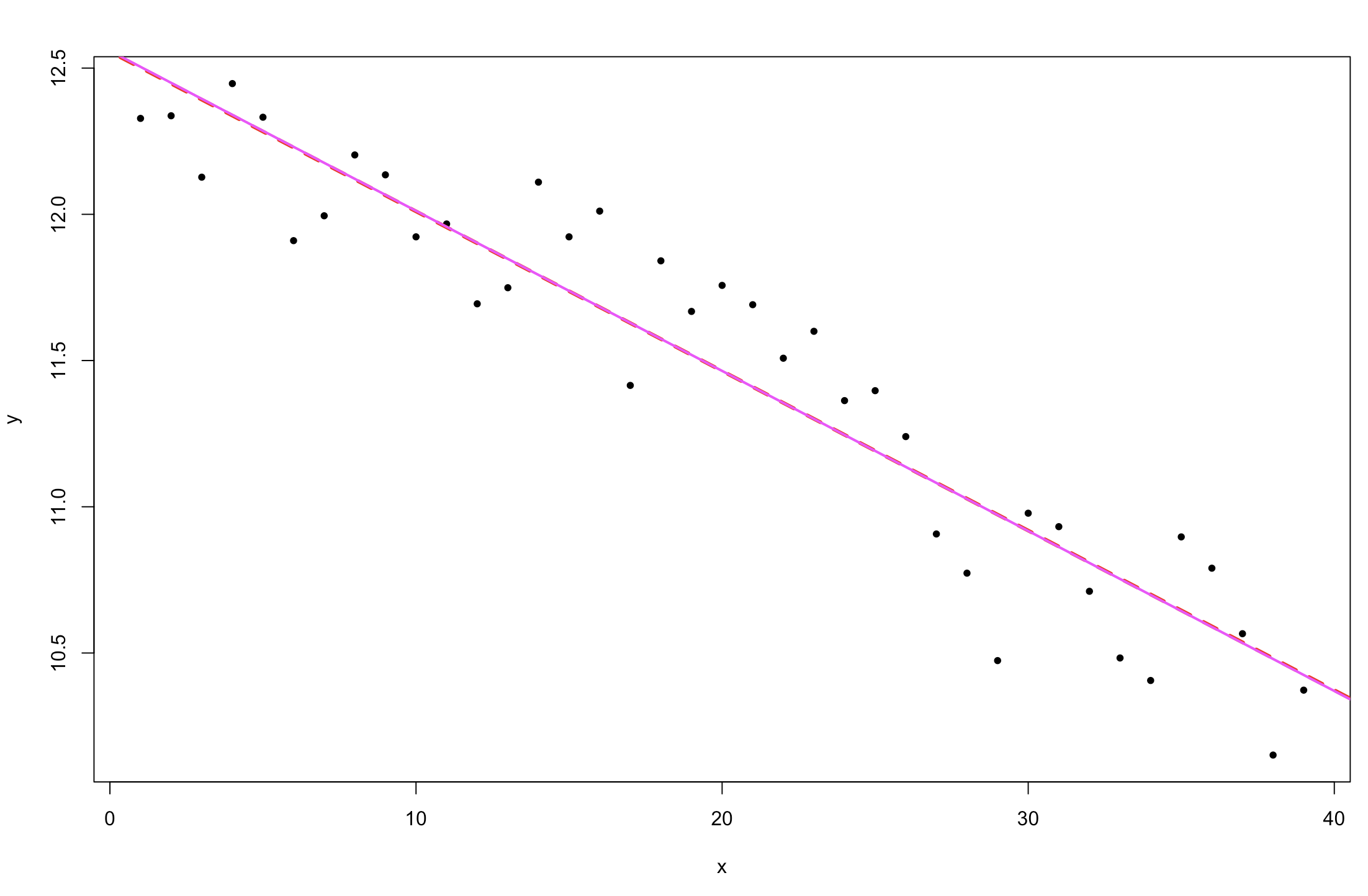
图 3. 北半球海冰范围随时间的变化(比较 Stan 线性模型拟合和一般 lm 拟合)。
结果与lm 输出相同 。这是因为我们使用了一个简单的模型,并且在我们的参数上放置了非信息先验。
将回归线估计中的可变性可视化的一种方法是绘制来自后验的多个估计。
plot(y ~ x, pch = 20)
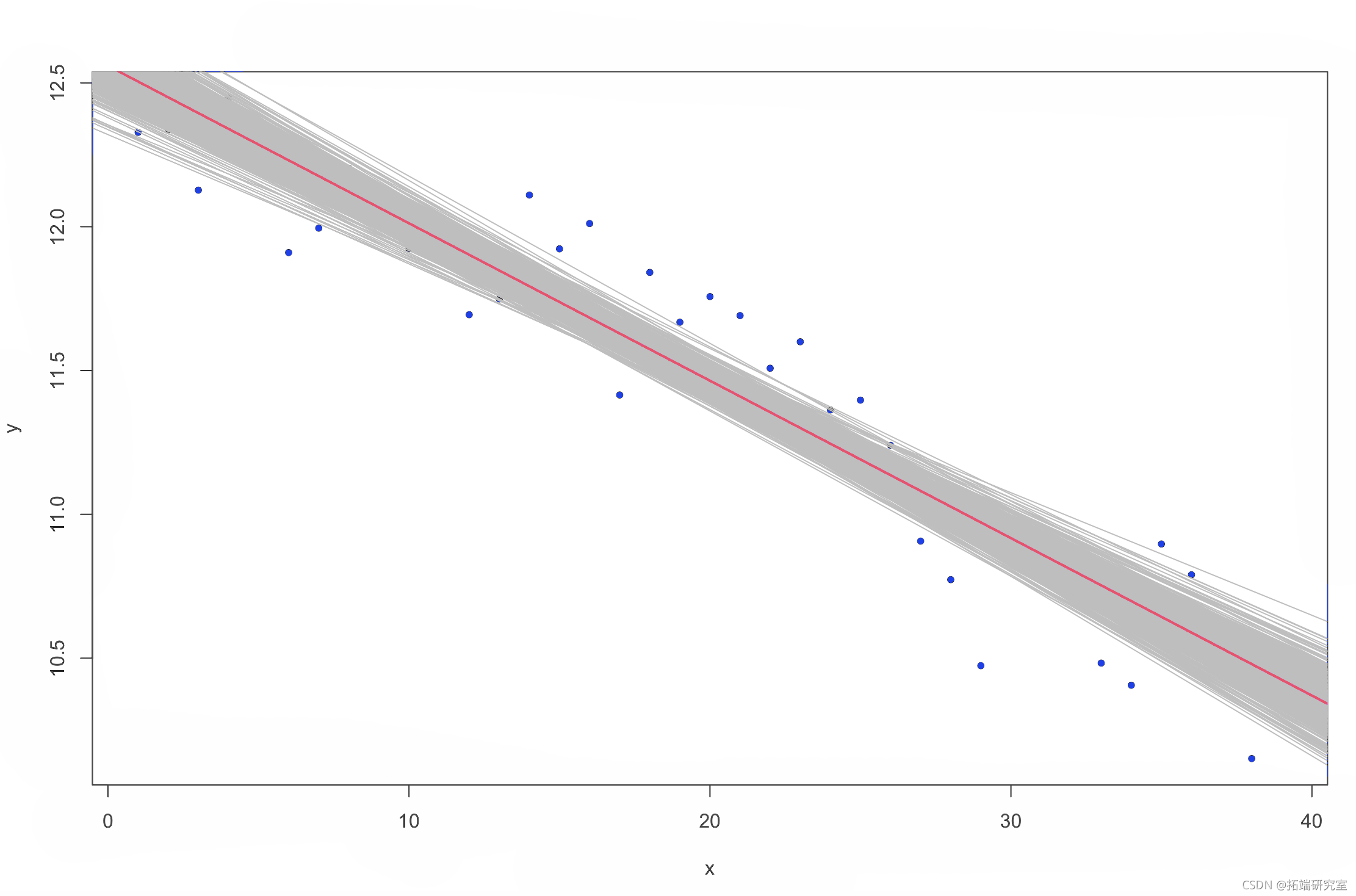 图 4. 北半球海冰范围随时间的变化(
图 4. 北半球海冰范围随时间的变化(Stan 线性模型拟合)。
5. 改变先验
我们再试一次,但现在对海冰和时间之间的关系采用更有信息量的预设。我们将使用小标准差的正态先验。如果我们使用标准差非常大的正态先验(比如1000,或者10000),它们的作用与均匀先验非常相似。
参数 real alha; // 截距 real bta; // 斜率(回归系数) real < lowr = 0 > sima; // 误差SD 模型 beta ~ nomal(1, 0.1); y ~ normal(apha + x * beta , siga);
我们将拟合该模型并将其与使用均匀先验的均值估计进行比较。
stan(stn_oel) plot(y ~ x)
图 5. 北半球海冰范围随时间的变化(Stan 线性模型拟合)。
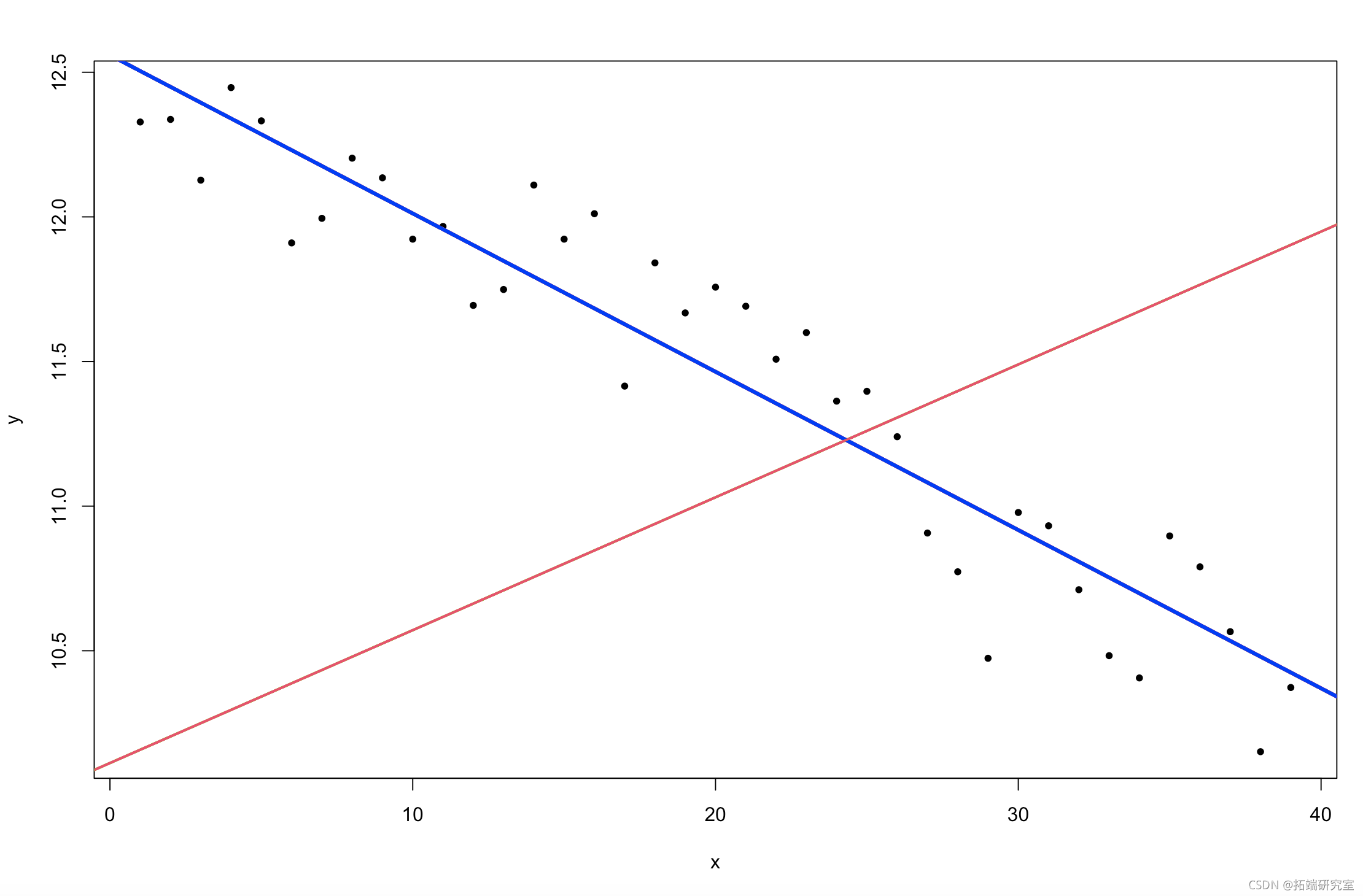
后验预测发生了什么变化?模型是否更好地拟合数据?为什么模型拟合发生了变化?通过制作非常窄的先验分布,我们的模型改变了什么?
尝试自己将先验更改为一些不同的数字,看看会发生什么,这是贝叶斯建模中的一个常见问题,如果您的先验分布非常窄,但不符合您对系统或数据分布的理解,您可以运行无法有意义地解释数据变化的模型。然而,这并不是说您不应该选择一些信息丰富的先验,您确实希望使用先前的分析和对您的研究系统的理解来告知您的模型先验和设计。您只需要仔细考虑您做出的每个建模决策!
6. 收敛诊断
在继续之前,我们应该再次检查模型参数的 Rhat 值、有效样本大小 ( n_eff) 和跟踪图,以确保模型已收敛且可靠。
n_f 是有效样本大小的粗略度量。通常只需要担心这个数字小于迭代次数的 1/100 或 1/1000。
对于跟踪图,我们可以直接从后验查看它们:
plot(alpha, type = "l") plot(beta, type = "l") plot(sigma, type = "l")
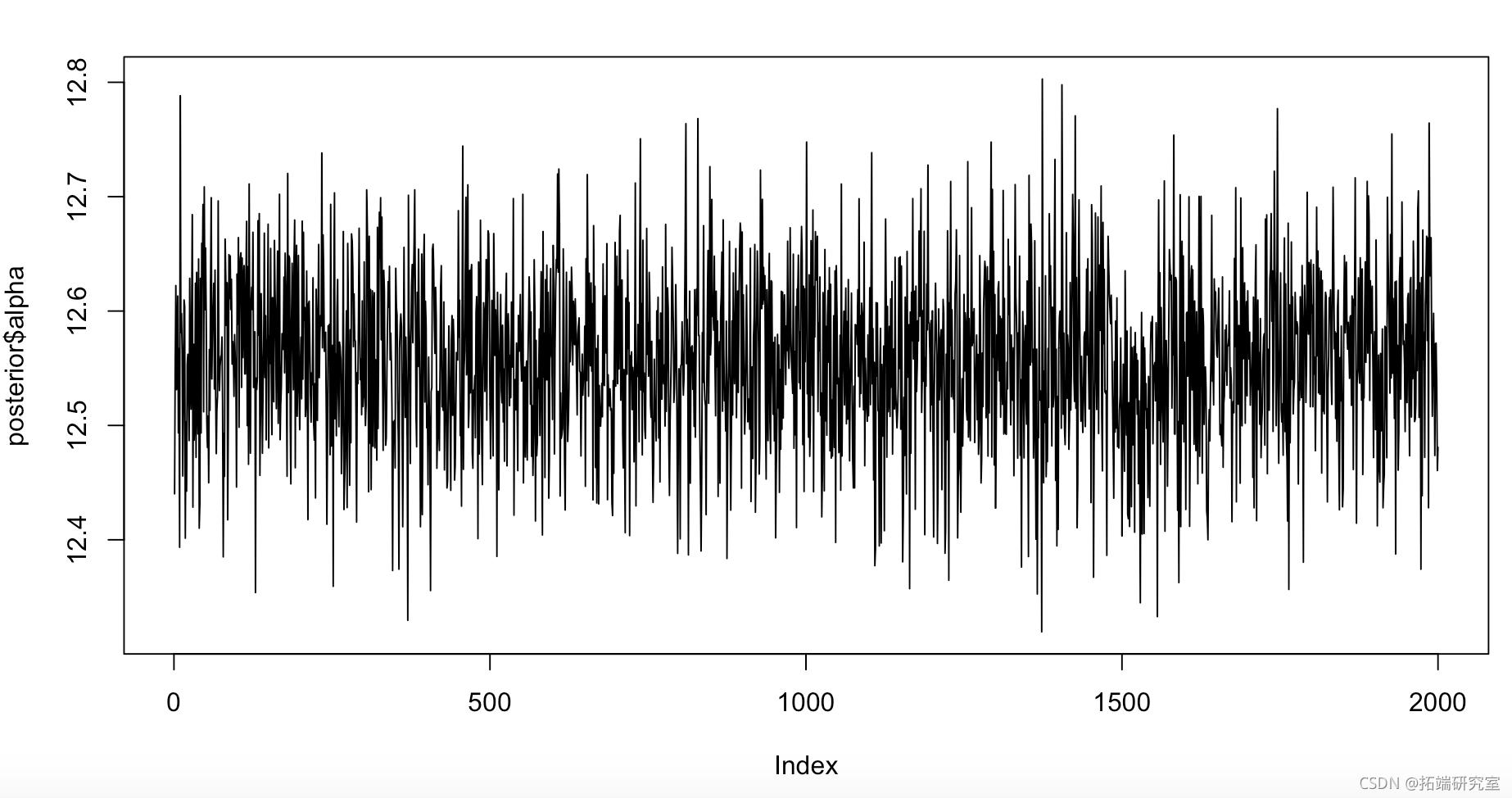 图 6. alpha 的迹线图,截距。
图 6. alpha 的迹线图,截距。
对于更简单的模型,收敛通常不是问题,除非您的代码中有错误,或者运行采样器的迭代次数太少。
收敛性差
尝试仅运行 50 次迭代的模型并检查跟踪图。
fid <- stan( iter = 50)
这在预热后也有一些“转换”,表明模型指定错误,或者采样器未能完全采样后验。
plot(alpha, type = "l") plot(beta, type = "l") plot(sigma, type = "l")
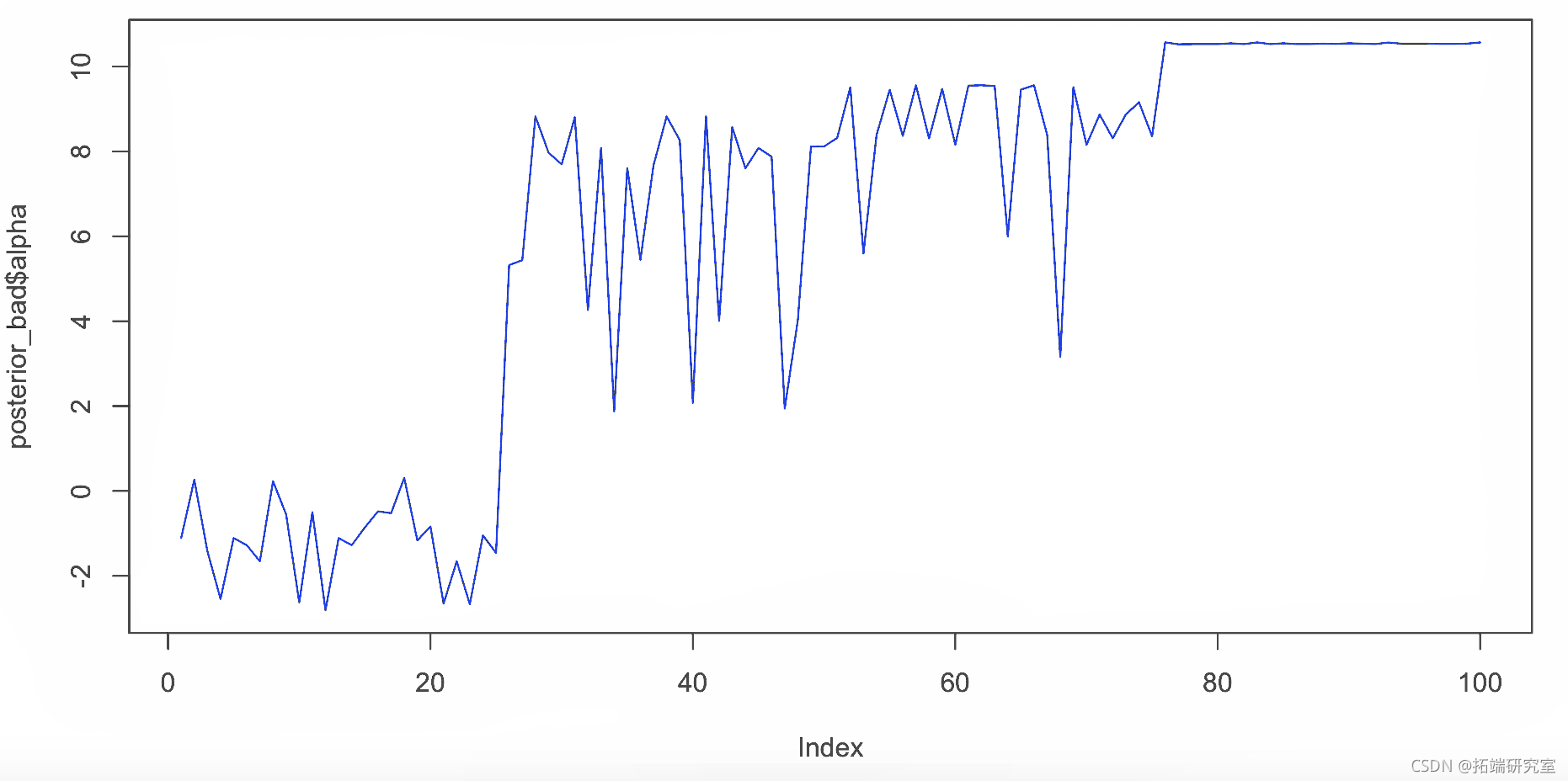 图 7. alpha 的错误轨迹图,截距。
图 7. alpha 的错误轨迹图,截距。
参数汇总
我们也可以直接通过后验得到参数的汇总。让我们还绘制非贝叶斯线性模型值,以确保我们的模型运行正确
par(mfrow = c(1,3)) plot(dnsty(alpha)
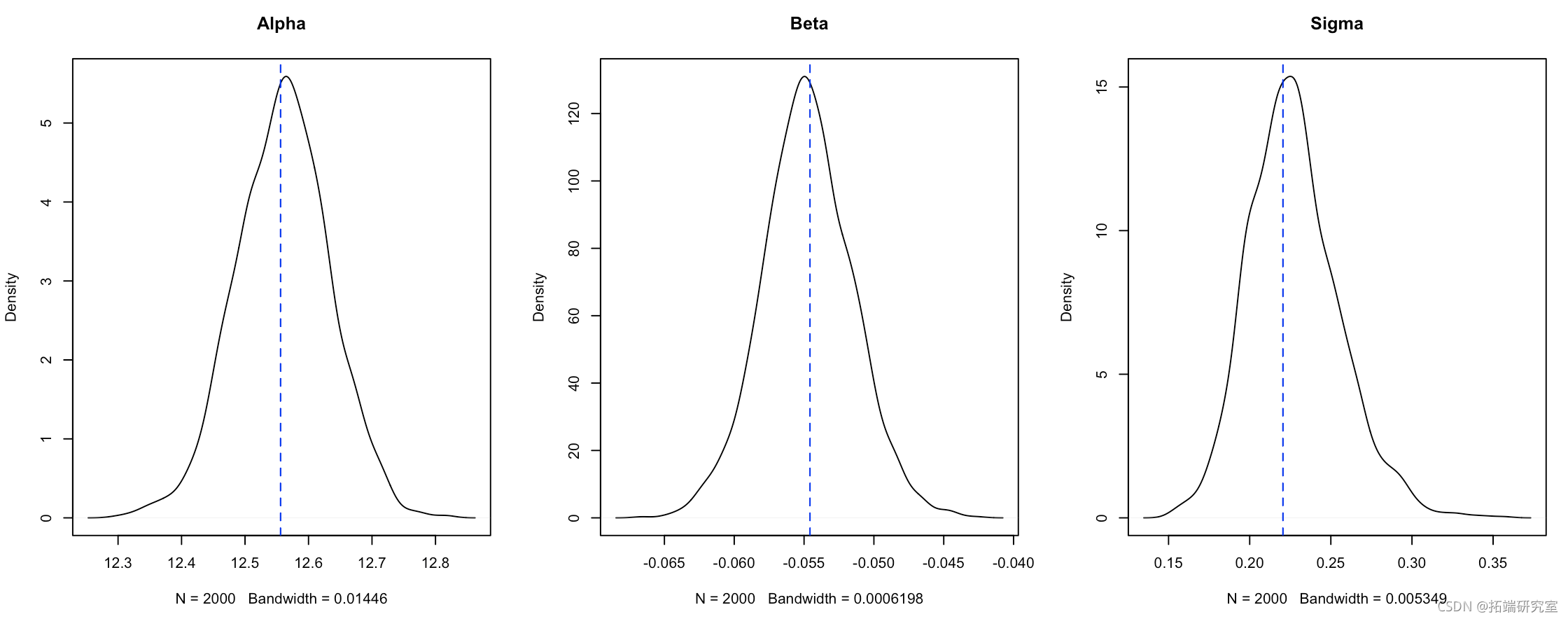 图 8.
图 8.Stan 模型拟合的密度图分布 与一般lm 拟合的估计值比较 。
从后验我们可以直接计算任何参数超过或低于某个感兴趣值的概率。
beta > 0 的概率:
sum(beta>0)/lenth(beta) # 0
beta > 0.2 的概率:
sum(bea>0.2)/legth(beta) # 0
诊断图 rstan
虽然我们可以直接使用后验,但 rstan 内置了许多有用的功能。
plot(fit)
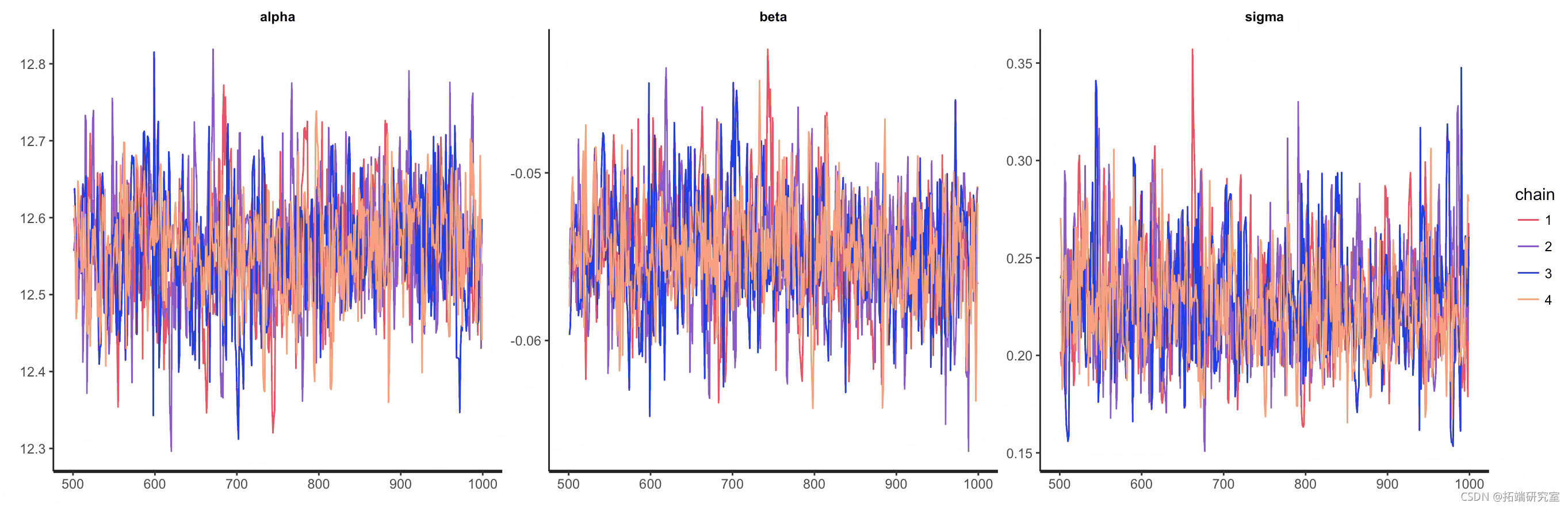 图 9.
图 9.Stan 模型不同链的跟踪图 。
我们还可以查看后验密度和直方图。
dens(it) hist(ft)
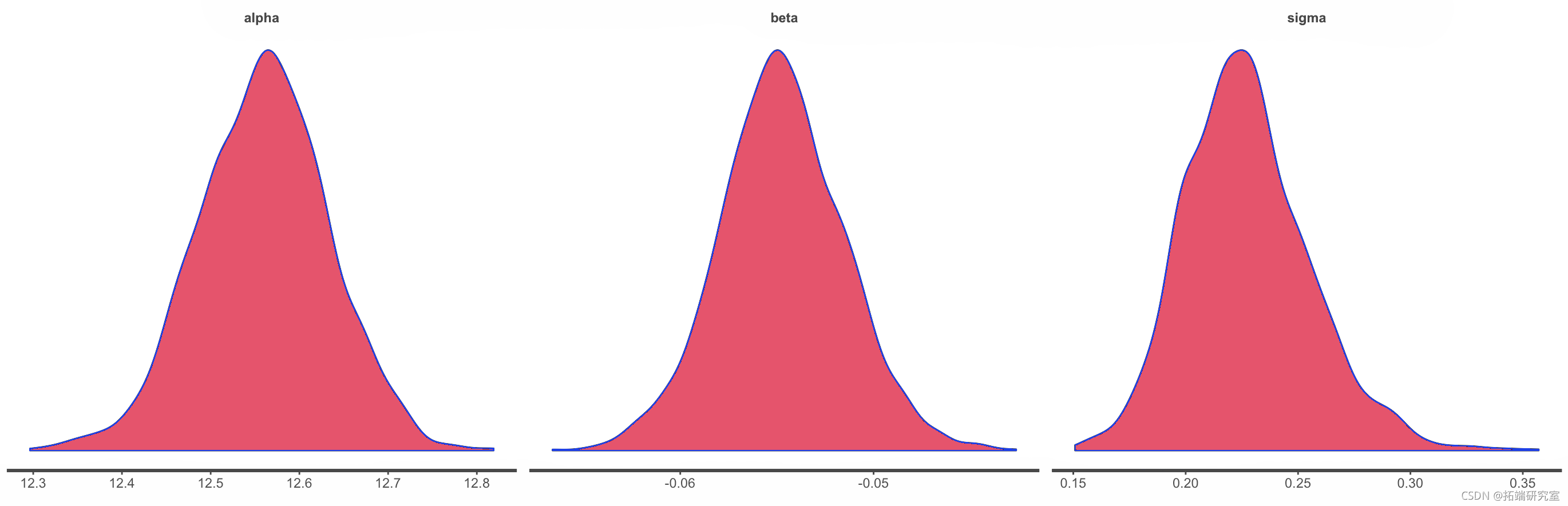
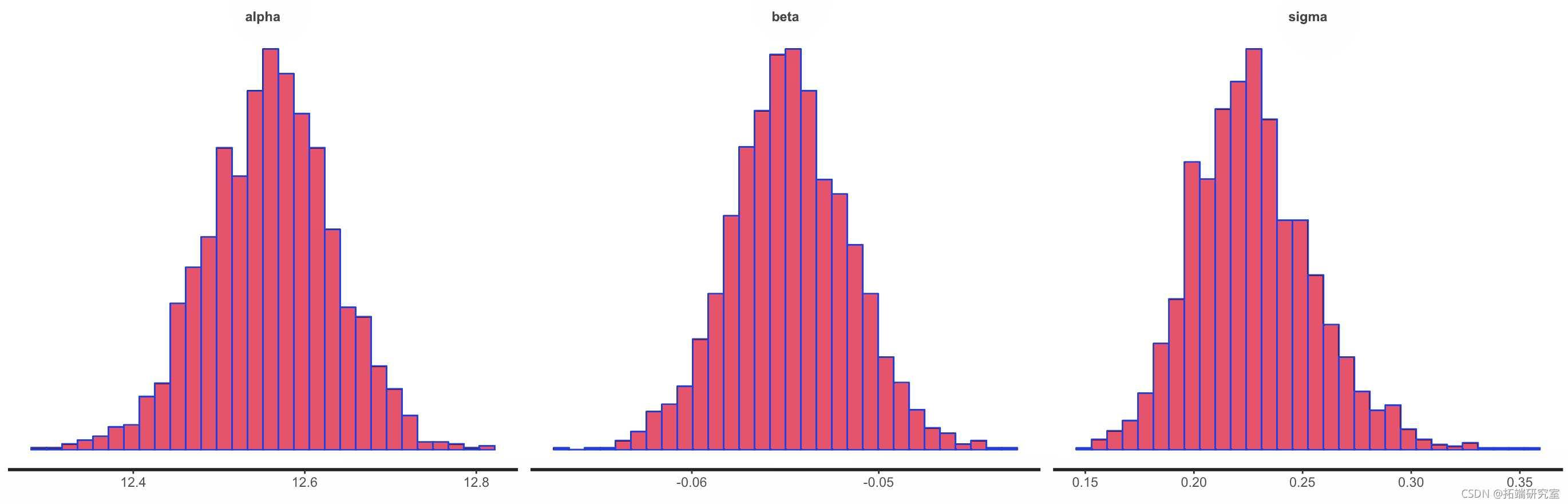 图 10.
图 10.Stan 模型中截距、斜率和残差方差的后验密度图和直方图 。
我们可以生成指示平均参数估计值和我们可能感兴趣的任何置信区间的图。请注意,beta 和 sigma 参数的 95% 置信区间 非常小,因此您只能看到点。根据您自己数据的差异,当您进行自己的分析时,您可能会看到更小或更大的置信区间。
plot(fit)
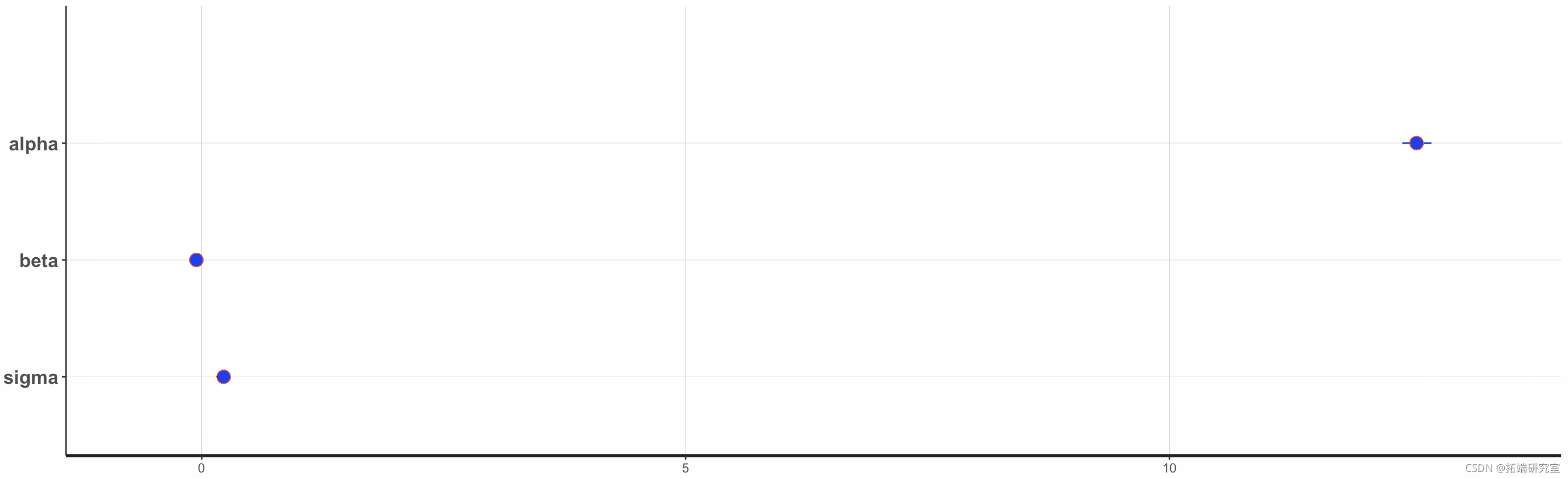 图 11.
图 11.Stan 模型的参数估计 。
后验预测检查
对于预测和作为模型诊断的另一种形式, Stan 可以使用随机数生成器在每次迭代中为每个数据点生成预测值。通过这种方式,我们可以生成预测,这些预测也代表了我们模型和数据生成过程中的不确定性。可用于获取我们想要的关于后验的任何其他信息,或对新数据进行预测。
参数
real alpha; // 截距
real beta; // 斜率(回归系数)
y ~ nomal(x * eta + alpa, sgma);
产生的数量
for (n in 1:N) {
yp\[n\] = normlrg(x\[n\] * bta + apha, sima) 。
}
请注意,GQ(生成量)块不支持矢量化,因此我们必须将其放入循环中。但是由于它被编译为 C++,循环实际上非常快,并且 Stan 每次迭代只评估一次 GQ 块,因此它不会为您的采样增加太多时间。通常,数据生成函数将是您在模型块中使用的分布,但带有 _rng 后缀。
stan(modl2GQ, data , ier = 1000, hans = 4, cres = 2, tin = 1)
y_rep 从后验中提取 值。
处理y_rep 值有很多选择 。
每一行都是模型的一次迭代(单一后验估计)。
我们可以制作一些更漂亮的图。这个包是ggplot2。
在200次后验抽样中,比较y的密度和y的密度。
poy(y, yrep\[1:200, \])
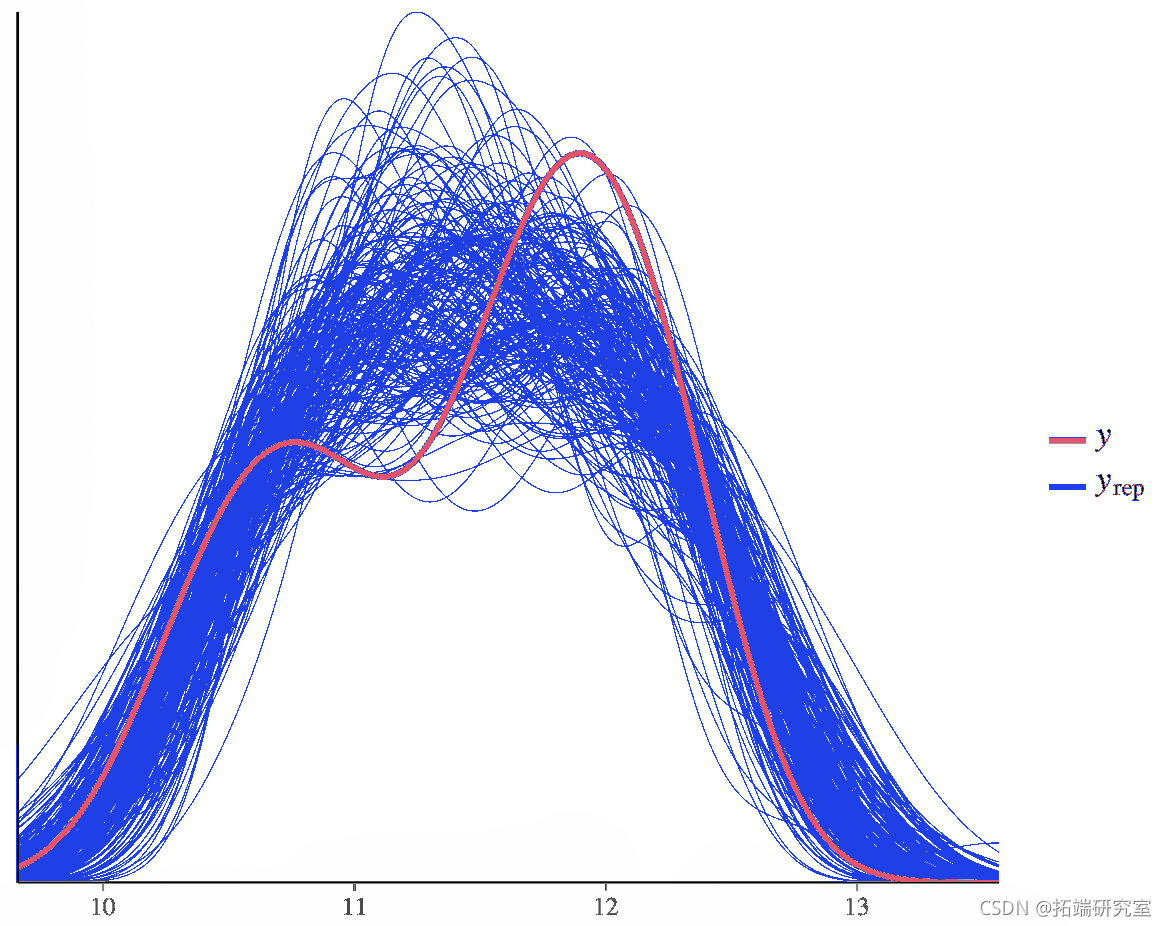 图 12. 比较随机后验抽取的估计值。
图 12. 比较随机后验抽取的估计值。
在这里,我们看到数据(深蓝色)与我们的后验预测非常吻合。
我们还可以使用它来比较汇总统计的估计值。
pp(y = y, yep = yrep, tat = "mean")
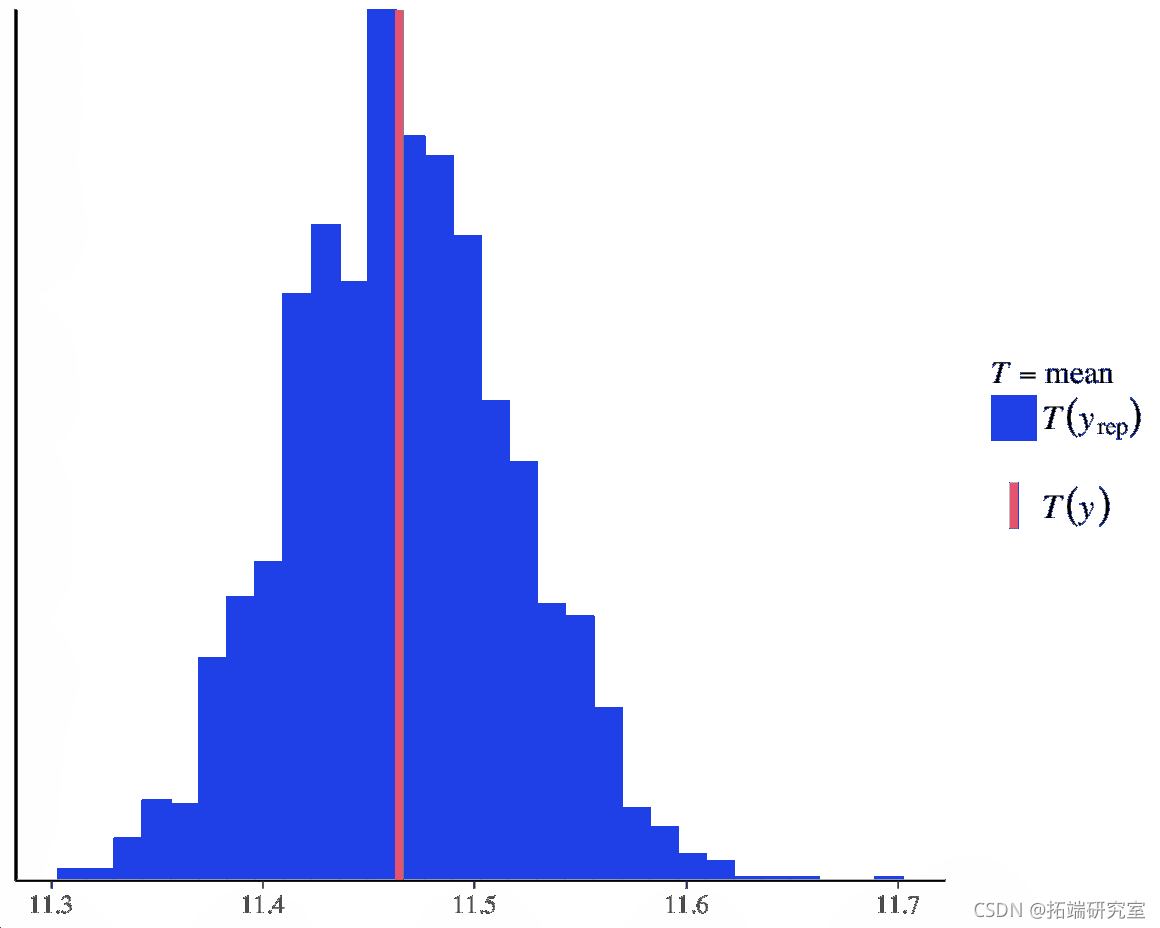
图 13. 比较汇总统计的估计值。
我们可以更改传递给 stat 函数的函数,甚至可以自己编写!
我们可以调查每个数据点的平均后验预测与每个数据点的观察值(默认线为 1:1)
scttrg(y = y, yrp = yrep)
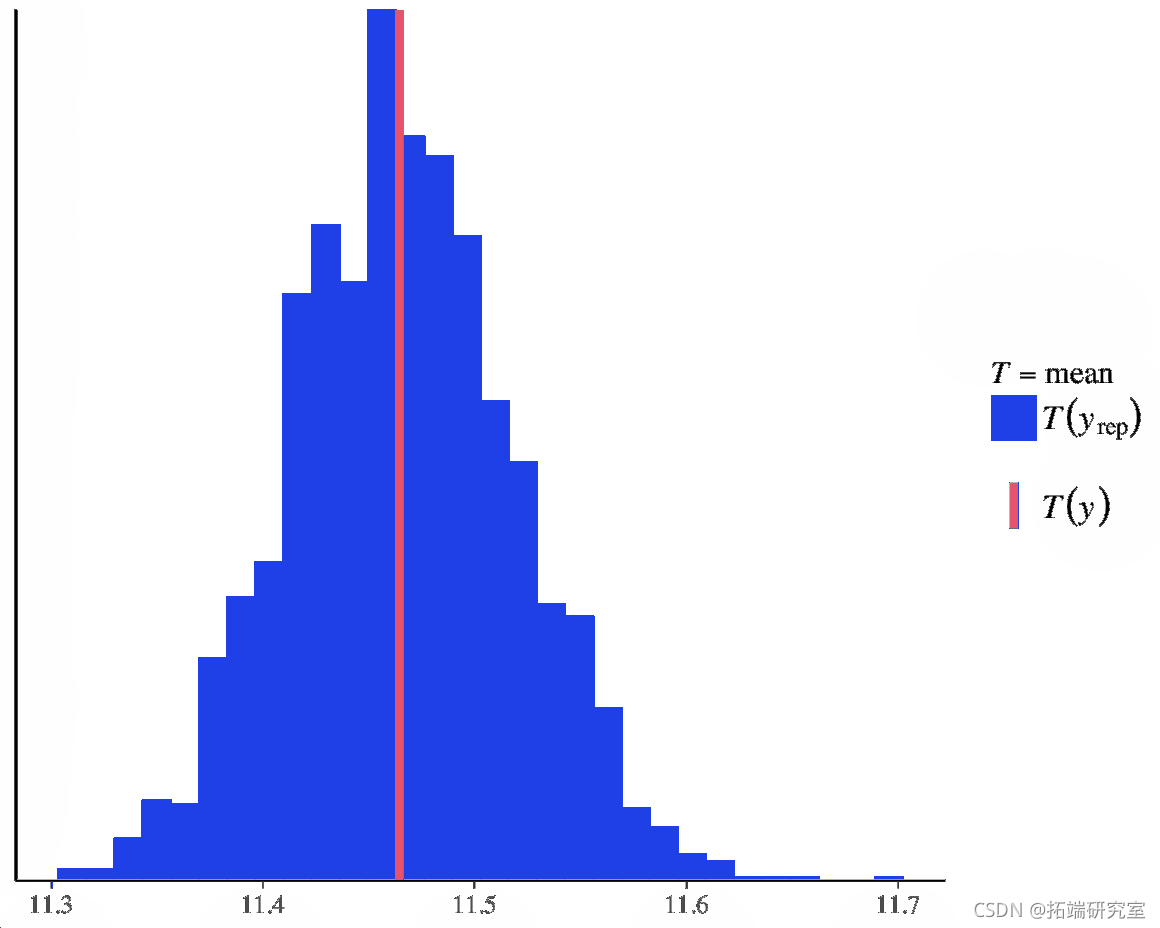 图 14. 每个数据点的平均后验预测与每个数据点的观测值。
图 14. 每个数据点的平均后验预测与每个数据点的观测值。
所以现在您已经学习了如何运行线性模型 Stan 并检查模型收敛性。
如有任何问题,请联系我们!
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 2026AI医疗行业专题报告:智能医疗器械、手术机器人、脑机接口、可穿戴设备|附240+份报告PDF、数据、可视化模板汇总下载
2026AI医疗行业专题报告:智能医疗器械、手术机器人、脑机接口、可穿戴设备|附240+份报告PDF、数据、可视化模板汇总下载



