混合线性模型,又名多层线性模型(Hierarchical linear model)。
它比较适合处理嵌套设计(nested)的实验和调查研究数据。
此外,它还特别适合处理带有被试内变量的实验和调查数据,因为该模型不需要假设样本之间测量独立,且通过设置斜率和截距为随机变量,可以分离自变量在不同情境中(被试内设计中常为不同被试)对因变量的作用。
可下载资源
简单的说,混合模型中把研究者感兴趣的自变量对因变量的影响称为固定效应,把其他控制的情景变量称为随机效应。由于模型中包括固定和随机效应,故称为混合线性模型。无论是用方差分析进行差异比较,还是回归分析研究自变量对因变量的影响趋势,混合线性模型比起传统的线性模型都有更灵活的表现。
首先看这个线性模型 y=a+bx+u,a为截距,b为回归系数,x为自变量,u为随机误差。这个模型中参数有a,b,u,3个参数中只有一个随机变量u,a,b是固定值。假设y为学生成绩,x为学生家庭背景,则u衡量的是每个具体学生和均值的成绩差异。
假设学校是从一个大的总体(比如一个省或者地区)中随机选取几个抽出来的。不同学校之间有差别,也就是每个学校的学生平均成绩是不同的,重点学校的学生基础好,所以整体水平高,差的学校学生整体水平不高。这个时候模型要修改为这样:y=a+uj+bx+u,a表示所有学校的平均成绩,uj表示每个具体的学校和所有学校平均成绩的差,好的学校这个差值为正,差的学校这个差值为负值。如果我们要研究所有学校的情况,那么uj要看成是随机变量,因为每次抽样,这个uj都是变化的。如果我们只研究抽出来的这几所学校,uj就是固定值。
y=a+uj+bx+u中uj看成是随机变量就是随机效应模型(因为模型中出现了随机效应),否则就是固定效应模型(因为模型中无随机效应)。
另外,y=a+bx+u模型中,如果假设a和b都是固定值,不随机,这个模型也是固定效应模型。我们平常见到的“经典线性回归”模型就是固定效应模型。
模型 y=a+bx+u 中参数有a和b,这两个参数我们一般认为是固定值,如果这两个参数中至少一个不固定,是随机变量,则模型就从固定效应模型变成了随机效应模型。对于所有学校来说如果a和b都一样,那么a和b就是固定值,如果每个学校的a或/和b都不同,那么a或/和b就是随机变量,它们的具体值随着学校而变化,模型就成了随机效应模型。
如果你还是觉得晕,不会辨别,那可以看模型中所有未知参数除了随机误差这个随机变量外,是否还有其它的未知参数是随机变量,如果有,则模型是随机效应模型,否则就是固定效应模型。
非线性混合模型就是通过一个连接函数将线性模型进行拓展,并且同时再考虑随机效应的模型。
非线性混合模型常常在生物制药领域的分析中会用到,因为很多剂量反应并不是线性的,如果这个时候数据再有嵌套结构,那么就需要考虑非线性混合模型了。
本文中我们用(非)线性混合模型分析藻类数据。这个问题的参数是:已知截距(0日值)在各组和样本之间是相同的。
数据
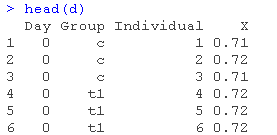
用lattice和ggplot2绘制数据。
xyplot(jitter(X)~Day, groups=Group)
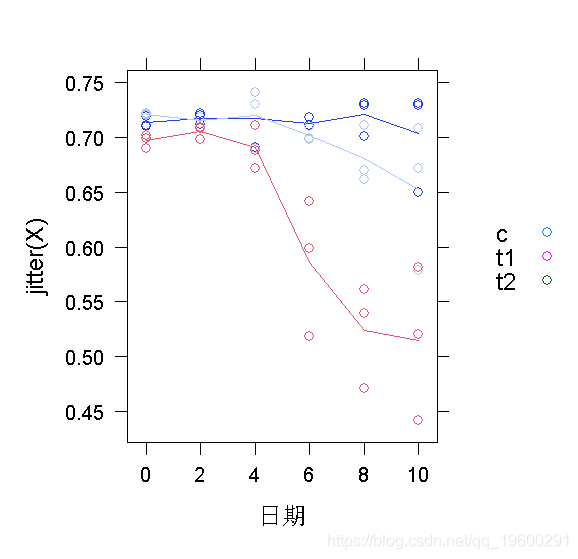
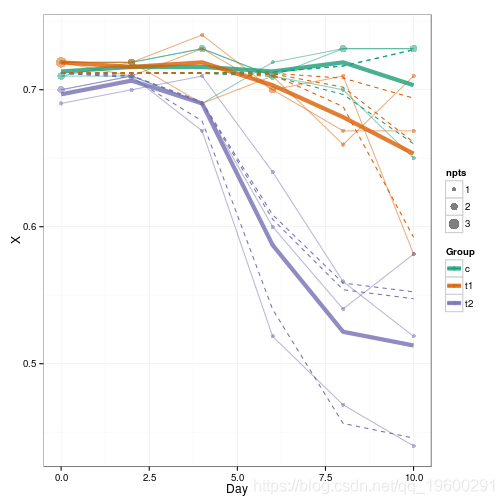
ggplot版本有两个小优势。1. 按个体和群体平均数添加线条[用stat_summary应该和用xyplot的type="a "一样容易]);2.调整点的大小,使重叠的点可视化。(这两点当然可以用自定义的 panel.xyplot 来实现 …)
## 必须用手进行汇总 ggplot(d,aes(x=Day,y=X,colour=Group))
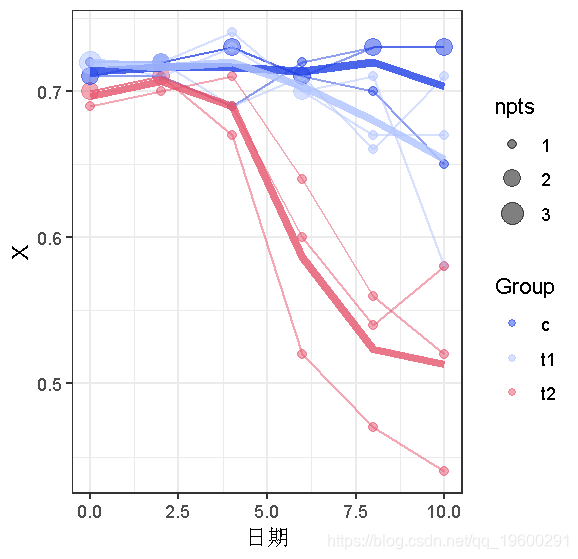
从这些图片中得出的主要结论是:(1)我们可能应该使用非线性模型,而不是线性模型;(2)可能存在一些异方差(在较低的平均值上有较大的方差,好像在 X=0.7的数据有一个 “天花板”);看起来可能存在个体间的变化(特别是基于t2的数据,其中个体曲线近乎平行)。然而,我们也将尝试线性拟合来说明问题。
使用nlme
用lme的线性拟合失败。
LME <- lme(X ~ 1, random = ~Day|Individual, data=d)

如果我们用control=lmeControl(msVerbose=TRUE))运行这个程序,就会得到输出,最后是。

可以看到考虑到组*日效应的模型也失败了。
LME1 <- lme(X ~ Group*Day, random = ~Day|Individual, data=d)

我试着用SSfpl拟合一个非线性模型,一个自启动的四参数Logistic模型(参数为左渐近线、右渐近线、中点、尺度参数)。这对于nls拟合来说效果不错,给出了合理的结果。
nlsfit1 <- nls(X ~ SSfp) coef(nlsfit1)

可以用gnls来拟合组间差异(我需要指定起始值
随时关注您喜欢的主题
我的第一次尝试不太成功。
gnls( X ~ SSfpl)

但如果我只允许asymp.R在各组之间变化,就能运行成功。
params=symp.R~Group
绘制预测值。
g1 + geom_line()
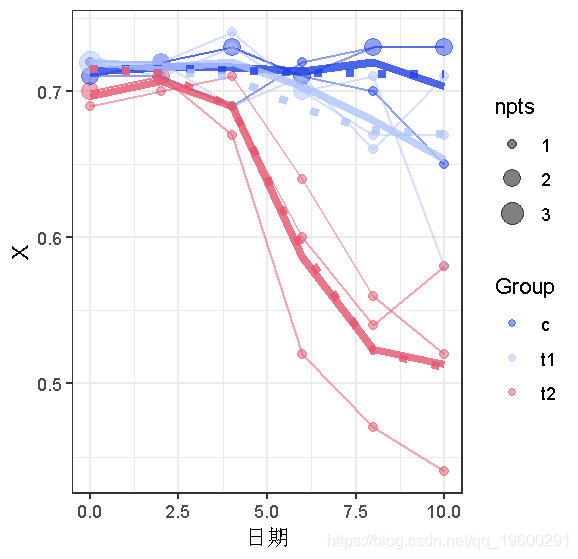
这些看起来很不错(如果能得到置信区间就更好了–需要使用delta法或bootstrapping)。
dp <- data.frame(d,res=resid(gnlsfit2),fitted=fitted(gnlsfit2)) (diagplot1 <- ggplot(dp,aes(x=factor(Individual), y=res,colour=Group))+ geom_boxplot(outlier.colour=NULL)+ scale\_colour\_brewer(palette="Dark2"))
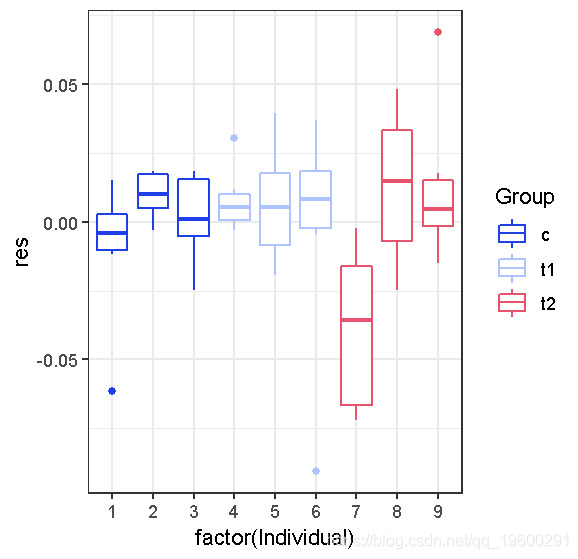
除了7号样本外,没有很多证据表明个体间的变异……如果我们想忽略个体间的变异,可以用
anova(lm(res~Individual))

大的(p\)值可以接受个体间不存在变异的无效假设…
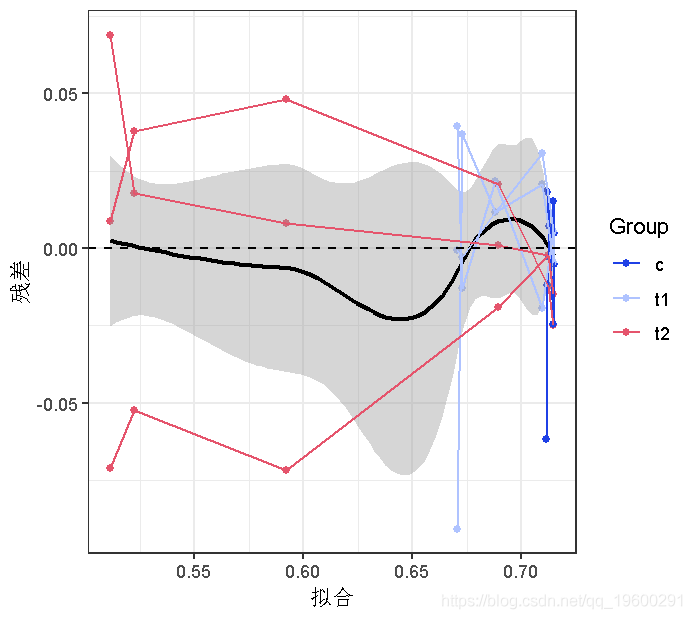
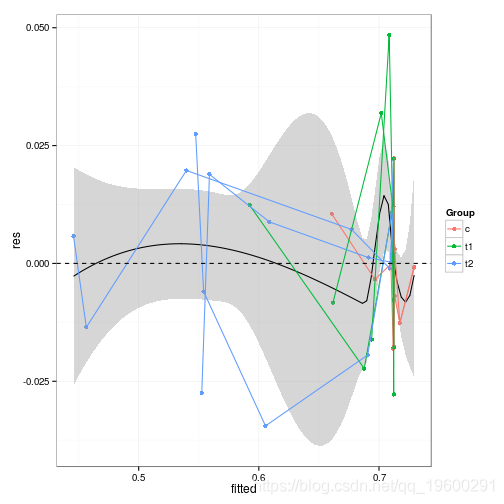
更一般的诊断图–残差与拟合,同一个体的点用线连接。可以发现,随着平均数的增加,方差会逐渐减小。
我不能用nlme来处理三个参数因组而异模型,但如果我只允许asymp变化,就可以运行。
plot(dp,(x=fitted,y=res,colour=Group))
nlme(model=list(fixed=with(c(asymp.R,xmid,scale,asymp.L),...)
右侧渐近线中的方差估计值是非零的。

加入随机效应后,参数根本就没有什么变化。
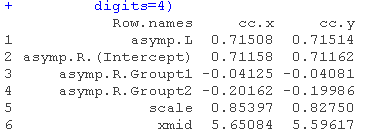
最大的比例差异是3.1%(在比例参数中)。
nlmefit2 <- update(list(asyR+xmd+scal+asp ~1), start )
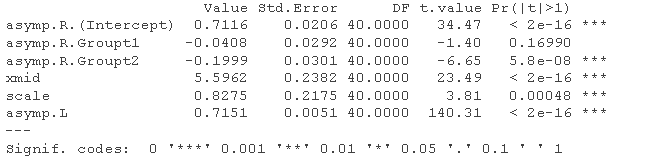
我们可以通过AIC或似然比检验来比较模型
AICtab(nlmefit1,nlmefit2,weights=TRUE)

anova(nlmefit1,nlmefit2)

可以做一个F测试而不是 LRT(即考虑到有限大小的修正)。
pchisq(iff,df=2,lower.tail=FALSE)

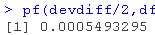
##分母非常大的F检验。 pf(diff/2,df1=2,df2=1000000,lower.tail=FALSE)

我们不知道真正相关的df,但上面的总结表明df是40。
nlmer
我想现在可以为nlmer得到正确的模型规范,但我找不到一个方便的语法来进行固定效应建模(即在这种情况下允许一些参数因组而异)–当我构建了正确的语法,nlmer无法得到答案。
基本的RE模型(没有群体效应)运行良好。
nlmer( X ~ SSfpl(Day, asy, as, x, s) ~ asy|Indi,)
根据我的理解,人们只需要构建自己的函数来封装固定效应结构;为了与nlmer一起使用,该函数还需要计算相对于固定效应参数的梯度。这有点麻烦,但可以通过修改派生函数生成的函数,使之稍微自动化。
- 构建虚拟变量:
mm <- model.matrix(~Group,data=d) grp2 <- mm\[,2\]
- 构建一个函数来评估预测值及其梯度;分组结构是硬编码的。
deriv(~A+((B0+B1\*grp2+B2\*grp3-A)/(1+exp((x-xmid)/scale)
- 通过插入与传递给函数的参数名称相匹配的行来查看所产生的函数,并将这些参数名称分配给梯度矩阵。
L1 <- grep("^ +\\\.value +<-")
L2 <- grep("^ +attr\\\(\\\.value",)
eval(parse(text))
尝试一下拟合:
nlmer( X ~ fpl(Day, asym, as, asymp, asR3, xmi, sca) ~ as|Indi, start = list(nlpars)),data=d)

失败了(但我认为这是由于nlmer本身造成的,而不是设置有什么根本性的问题)。为了确定,我应该按照同样的思路生成一个更大的人工数据集,看看我是否能让它工作起来。
现在我们可以用稳定版(lme4.0)得到一个答案。
结果不理想
fixef(nlmerfit2)

range(predict(nlmerfit2))
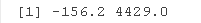
我不能确定,在nlmer中是否有更简单的方法来做固定效果。
AD模型生成器
我们还可以使用AD模型生成器来解决这个问题。它可以处理更复杂的模型,比如拟合更多参数的群体效应。
部分原因是我对ADMB的熟悉程度较低,这有点费劲,最后我通过循序渐进的步骤才成功。
最小的例子
首先尝试没有随机效应、分组变量等。(即等同于上面的nls拟合)。)
##设置数据:调整名称,等等
d0 <- c(list(nobs=nrow(d)),as.list(d0))
##起始值:调整名称,增加数值
names(svec3) <- gsub("\\\.","",names(svec3)) ## 移除点
svec3$asympR <- 0.6 ## 单一值
## 运行
do_admb("algae0",
data,
params,
run.opts)
结果不错
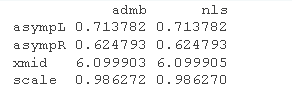
固定效应模型
现在尝试用固定效应分组,使用上面构建的虚拟变量(也可以使用if语句,或者用R[Group[i]]的for循环中的R值向量,或者(最佳选择)为R传递一个模型矩阵…)。我们必须使用elem_div而不是/来对两个向量进行元素除法。
model1 <- " 参数部分 向量 pred(1,nobs) // 预测值 向量Rval(1,nobs) //预测值 过程部分 pred = as+elem(Rval-asy,1.0+exp(-(Day-xmid)/scal) "
试着用模型矩阵来代替它。
model1B <- " 参数部分 向量 pred(1,nobs) // 预测值 向量Rval(1,nobs) //预测值 过程部分 pred = asym+ele(Rv-asy,1.0+exp(-(Da-xmi)/sc)) 。 "
当然,在参数相同的情况下,也可以工作。
随机效应
现在添加随机效应。回归函数并没有完全实现随机效应模型(尽管这应该在即将到来的版本中被修复),所以我们用公式减去(n/2 log({RSS}/n)),其中RSS是残差平方和。
model2 <- " 参数部分 向量 pred(1,nobs) // 预测值 向量Rval(1,nobs) //预测值 过程部分 pred = asym+elem f = 0.5\*no\*log(norm2(X-pr)/n)+norm2(R)。 "

由于ADMB不处理稀疏矩阵,也不惩罚循环,如果将随机效应实现为(i=1; i<=nobs; i++) Rval[i] += Rsigma*Ru[Group[i]],效率会略高,但我是懒人/我喜欢矩阵表示的紧凑性和可扩展性.
现在我们终于可以测试R以外的参数的固定效应差异了。
model3 <- " 参数部分 向量 prd(1,nobs) // 预测值 向量Rl(1,nobs) // 预测值 向量 scalal(1,nobs) 向量xmal(1,nobs) sdror opr(1,nobs) //输出预测值 程序部分 Rval = XR\*Rve+Rsma\*(Z*Ru)。 xmval = Xd*xdvec;.... f = 0.5\*nobs\*log(norm2(X-pred)/nobs)+norm2(Ru) "
结果:

summary(admbfit3)
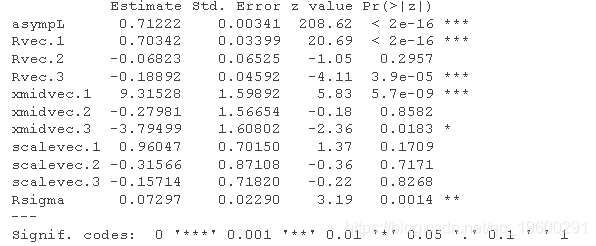
有一个非常大的AIC差异。如上文所示,对nlme拟合的似然比F测试是作为一种练习……
对于该图,最好是按组指定参数重新进行拟合,而不是按基线+对比度进行拟合。
fit3B <- do_admb(, data, params, re, run.opts=run.control)
plot2(list(cc),intercept=TRUE)
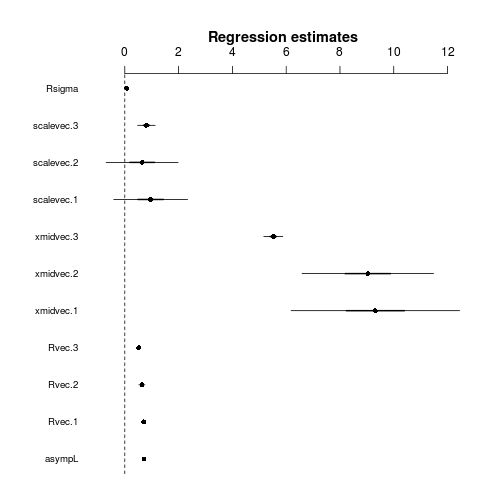
现在我们对标准化的问题很困扰,所以(经过一番折腾)我们可以在不同的面板上重新画出群体变化的参数。
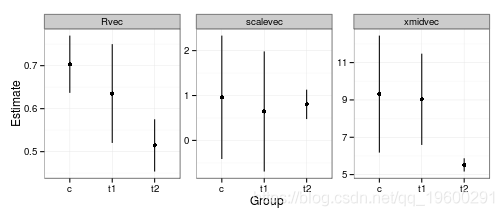
诊断图
##放弃条件模式/样本-R估计值 diagplot1 %+% dp2
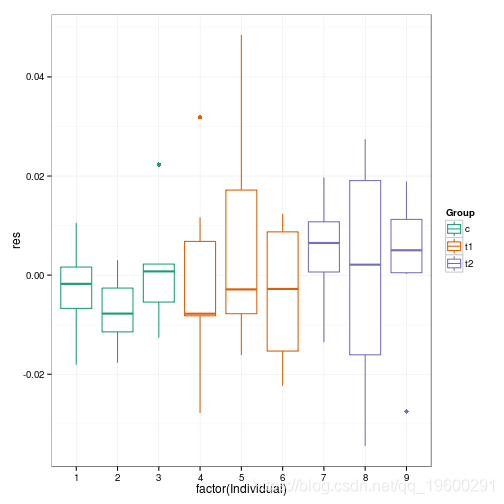
也许这暗示了两个实验组中更大的差异?
拟合与残差
diagplot2 %+% dp2
叠加预测(虚线):
g1 + geom_line
如果能生成平滑的预测曲线(即对中间的日值),那就更好了,但也更繁琐。
结论
- 从参数估计中得出的主要结论是,第三组下降得更早一些(xmidvec更小),同时下降得更远(Rvec更低)。
似然分析
计算一个( sigma^2_R ) 似然函数的代码并不难,但运行起来有点麻烦:它很慢,而且计算在置信度下限附近的几个点上出现了非正-无限矩阵;我运行了另一组值,试图充分覆盖这个区域。
lapply(Rsigmavec,fitfun) ## 尝试填补漏洞 lapply(Rsigmavec2,fitfun)
带有插值样条的剖面图和似然比检验分界线。
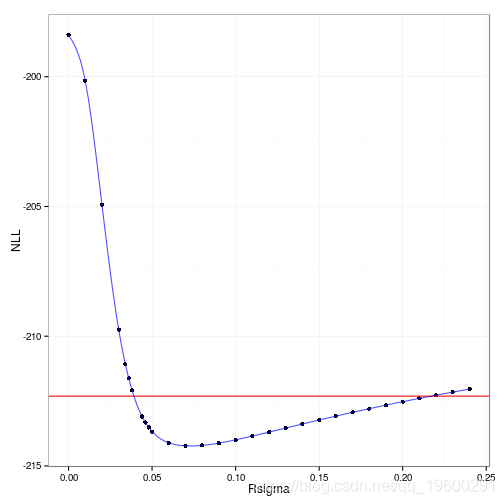
在sigma^2_R 上的95%剖面置信区间是{0.0386,0.2169}。
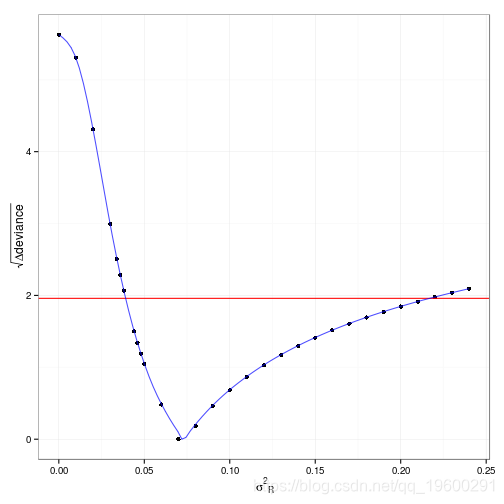
我没有计算过,但转换后的剖面图(在对应于偏离度与最小偏离度的平方根偏差的 y )上,所以二次剖面将是一个对称的V)显示,二次近似对这种情况相当糟糕 …
ggplot(sigma,sqrt(2*(NLL-min(NLL))+ geom_point()
扩展
- 更多地讨论分母df问题。参数bootstrap法/MCMC?
- 我们可以尝试在xmid和scale参数中加入随机效应。
- 在组间或作为X的函数的方差(无论是残差还是个体间的方差)中可能有额外的模式。

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 Python用Lasso改进线性混合模型Linear Mixed Model分析拟南芥和小鼠复杂性状遗传机制多标记表型预测可视化
Python用Lasso改进线性混合模型Linear Mixed Model分析拟南芥和小鼠复杂性状遗传机制多标记表型预测可视化 R语言MCMC的lme4二元对数Logistic逻辑回归混合效应模型分析吸烟、喝酒和赌博影响数据
R语言MCMC的lme4二元对数Logistic逻辑回归混合效应模型分析吸烟、喝酒和赌博影响数据 R语言贝叶斯广义线性混合(多层次/水平/嵌套)模型GLMM、逻辑回归分析教育留级影响因素数据
R语言贝叶斯广义线性混合(多层次/水平/嵌套)模型GLMM、逻辑回归分析教育留级影响因素数据 R语言因子实验设计nlme拟合非线性混合模型分析有机农业施氮水平
R语言因子实验设计nlme拟合非线性混合模型分析有机农业施氮水平
