现在有了对贝叶斯方法的概念理解，我们将实际研究使用它的回归模型。
为了简单起见，我们从回归的标准线性模型开始。
然后添加对采样分布或先验的更改。
与 OLS 相比，我们有一个模型参数的后验分布，它与数据的似然和参数的先验概率的乘积成正比。在此，我们可以看到贝叶斯线性回归主要的两个好处。
先验分布：如果具备领域知识或者对于模型参数的猜测，我们可以在模型中将它们包含进来，而不是像在线性回归的频率方法那样：假设所有关于参数的所需信息都来自于数据。如果事先没有没有任何的预估，我们可以为参数使用无信息先验，比如一个正态分布。后验分布：使用贝叶斯线性回归的结果是一个基于训练数据和先验概率的模型参数的分布。这使得我们能够量化对模型的不确定性：如果我们拥有较少的数据点，后验分布将更加分散。
随着数据点的增加，似然会降低先验的影响，当我们有无限的数据时，输出的参数会收敛到从 OLS 方法获得的值。
将模型参数作为概率分布的公式反映了贝叶斯学派的世界观：我们从最初的估计和先验分布开始，并随着收集到更多的证据，模型会变得更少犯错。贝叶斯推理是我们直觉的自然延伸。通常，我们有一个初始的假设，并且随着收集到那些或支持、或否定想法的数据越来越多，我们对于世界的模型将会发生改变（理想情况下，这就是我们进行推理的方式）。
我们将通过 R 和相关的 R 包 rstan 使用编程语言 Stan。
示例：线性回归模型
在下文中，我们将设置一些初始数据，并使用标准 lm 函数运行模型比较。
设置
首先，我们需要创建我们将在此处使用的数据以及本文档中的大多数其他示例。
`````` # 为stan输入创建数据列表对象 dat = list
接下来是 Stan 代码。在 R2OpenBugs 或 rjags 中，可以使用代码调用单独的文本文件，并且可以对 rstan 执行相同操作，但出于我们的目的，我们在 R 代码中显示它。首先要注意的是模型代码。
接下来，Stan 有必须按顺序调用的编程块。我将在代码中列出所有块来记录它们的顺序并依次讨论每个块，即使我们不会全部使用它们。
// 或 # 之后或 // 之间的任何内容都是与代码相关的注释。而分布用 ∼∼ 指定，例如， y ~ normal(0, 1) 表示 y 正态分布，均值为 0，标准差为 1。
可下载资源
此外，要安装 rstan，需要通过 CRAN 或 GitHub。它不需要单独安装 Stan 本身，但它确实需要几个步骤并且需要 C++ 编译器。一旦你安装了 rstan，它就会像任何其他 R 包一样被调用。
# 使用语法创建模型对象
stanmodelcode = "
data { // 数据块
int<lower=1> N; // 样本大小
int<lower=1> K; // 模型矩阵的尺寸
/*
转换后的数据 { // 转换后的数据块。目前不使用。
}
*/
参数// 参数块
real<lower=0> sigma; // 误差比例
}
模型 // 模型块
mu = X * beta; // 创建线性预测器
// 先验指标
sigma ~ cauchy(0, 5); // 由于sigma被限定在0
// 似然
y ~ normal(mu, sigma);
/*
生成的数量 { // 生成的数量块
Stan代码
第一部分是数据块，我们告诉 Stan 它应该从数据列表中获得的数据。设置边界作为对数据输入的检查，这就是 < > 。
声明的前两个变量是 N 和 K，都是整数。接下来代码分别声明模型矩阵和目标向量。
我们声明变量的类型和维度，然后声明其名称。在 Stan 中，在一个块中声明的所有内容都可用于后续块，但在一个块中声明的内容可能不会在更早的块中使用。即使在一个块中，任何声明的东西，例如 N 和 K, 然后可以随后使用，就像我们指定模型矩阵的维度一样 X。
作为参考，以下内容来注明了感兴趣的变量以及将在其中声明它们的相关块。
| 种类 | 声明块 |
|---|---|
| 建模的，未建模的数据 | 数据，转换后的数据 |
| 建模参数，缺失数据 | 参数，转换参数 |
| 未建模参数 | 数据，转换后的数据 |
| 产生量 | 转换数据、转换参数、生成量 |
| 循环索引 | 循环语句 |
转换后的数据块是您可以执行对数或中心化等类似操作的地方，即您可以根据输入数据或一般情况下创建新数据。但是，如果您使用的是 R，那么首先在 R 中执行这些操作并将它们包含在数据列表中。您还可以在此处声明任何未建模的参数，例如您希望固定为某个值的参数。
要估计的主要感兴趣的参数位于参数块中。与数据块一样，您只能声明这些变量，不能进行任何赋值。在这里，我们注意到要估计的 β 和 σ，后者的下限为零。在实践中，如果截距或其他系数在显着不同的尺度上，您可能更愿意将它们分开建模。
转换后的参数块是可能包含可选参数的地方。为了提高效率，您通常只想放置依赖于参数块的特定兴趣的东西。
随时关注您喜欢的主题
模型块是指定您的先验和可能性以及任何必要变量的声明的地方。例如，此处包含线性预测器，因为它将趋向于似然. 请注意，我们可以将线性预测器放在转换后的参数部分，但这会减慢过程，而且我们对这些特定值不太感兴趣。
我对系数使用的是正态先验，平均值为零，标准差很大。对于σ的估计，我使用的是Cauchy 分布。许多使用BUGS的回归例子都会使用反伽马先验，这对这个模型来说是完全可以的，尽管它对其他方差参数的效果并不理想。如果我们没有为参数的先验分布指定任何东西，均匀分布将是默认的。
最后，你想计算的任何东西都可以放在这里–对新数据的预测、参数的比率、参数大于x的次数、为报告目的的参数转换等等。我们稍后将对此进行演示。
运行模型
现在我们对代码的作用有了一个概念。贝叶斯估计，像最大似然法一样，以初始猜测为起点，然后以迭代的方式运行，每一步都从后验分布中产生模拟抽样，然后纠正这些抽样，直到最后达到某个目标，或平稳分布。
这一部分是关键，与经典的统计学不同。我们的目标是一个分布，而不是一个点估计。
这个模拟过程被称为马尔科夫链蒙特卡洛，简称MCMC。这个过程的具体细节使许多贝叶斯编程语言/方法与众不同。在MCMC中，所有来自后验的模拟抽样都是基于以前的抽样并与之相关的，因为这个过程是沿着走向平稳分布的道路前进的。我们通常会让这个过程预烧，或者说从最初的起点开始有点稳定下来，这可能会有很大的偏差，因此在最初的几次迭代中，后续的估计值也会有很大的偏差。然而，作为进一步的检查，我们将多次运行整个过程，也就是说，有一个以上的链。由于这些链将从不同的地方开始，如果多个链最后都到达了同一个结果，我们就可以对结果更有信心。
你会注意到Stan将其代码编译为C++的时间可能比运行模型的时间要长，而在我的电脑上，每条链只需要一秒钟多一点的时间。然而，贝叶斯方法曾经需要很长的时间，即使是像这样的标准回归，这也许是贝叶斯分析在过去几十年里才流行起来的主要原因；我们根本没有机器来有效地做这件事。即使是现在，对于高度复杂的模型和大数据集来说，它仍然需要很长的时间来运行，尽管通常不会太长。
在下面的代码中，我们注意到包含stan模型代码的对象
数据列表，我们想要多少次迭代（5000），我们想要这个过程在开始保留任何估计值之前运行多长时间（warmup=2500），我们想要保留多少次后验的抽取（thin=10意味着每十次抽取），以及链的数量（chains=4）。最后，我们将有四条链，从参数的后验分布中抽取1000次。即使在verbose = FALSE的情况下，Stan也会向R控制台输出大量的输出，我在这里省略，但是你会看到一些关于编译过程的初始信息，当每条链通过iter参数中指定的10%的迭代时的更新，以及最后对耗时的估计。你可能还会看到一些信息，除非它们是高度重复的，否则不应该被视为错误。
`````` # 摘要 print(fit
到目前为止还不错。平均估计值反映了感兴趣的参数的后验结果的平均值，是标准回归分析中报告的典型系数。值得注意的是95%的概率或置信区间，因为它们不是你所知道的置信区间。这里没有重复抽样的解释。概率区间是更直观的。
它的意思很简单，根据这个模型的结果，真实值有95%的可能性会落在这两点之间。
将这些结果与R的lm函数的结果相比较，我们可以看到我们得到了类似的估计值，因为它们在小数点后两位是相同的。事实上，如果我们使用统一先验，模型与用标准最大似然估计所做的基本相同。在这里，对于一个并不复杂的模型来说，我们有相当多的数据，所以我们会期望可能性明显超过先验。
summary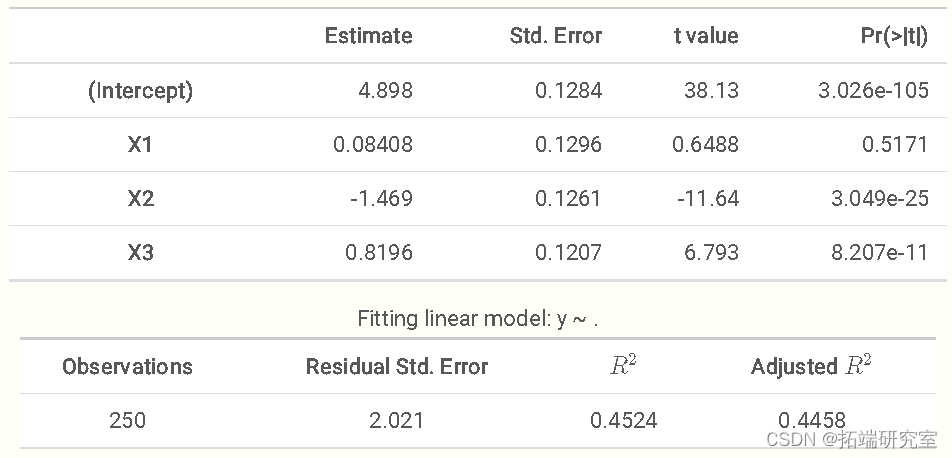
但是我们怎么知道我们的模型是否运作良好呢？有几个标准的诊断方法，但让我们看一下目前的一些情况。在摘要中，se_mean是蒙特卡洛误差，是对只有有限数量的后验抽样所带来的不确定性的估计。n_eff是给定所有链的有效样本量，基本上占了链中的自相关，即当我们从一次抽样到下一次抽样时估计的相关性。它实际上不需要很大，但如果它相对于所需的总抽样数来说很小，那就可能引起关注了。 Rhat是衡量链的混合程度的指标，当链被允许运行无限次抽样时，它就会变成1。在这种情况下，n_eff和Rhat表明我们有很好的收敛性，但我们也可以用跟踪图来直观地检查。
# 视觉化 srace(fit'))
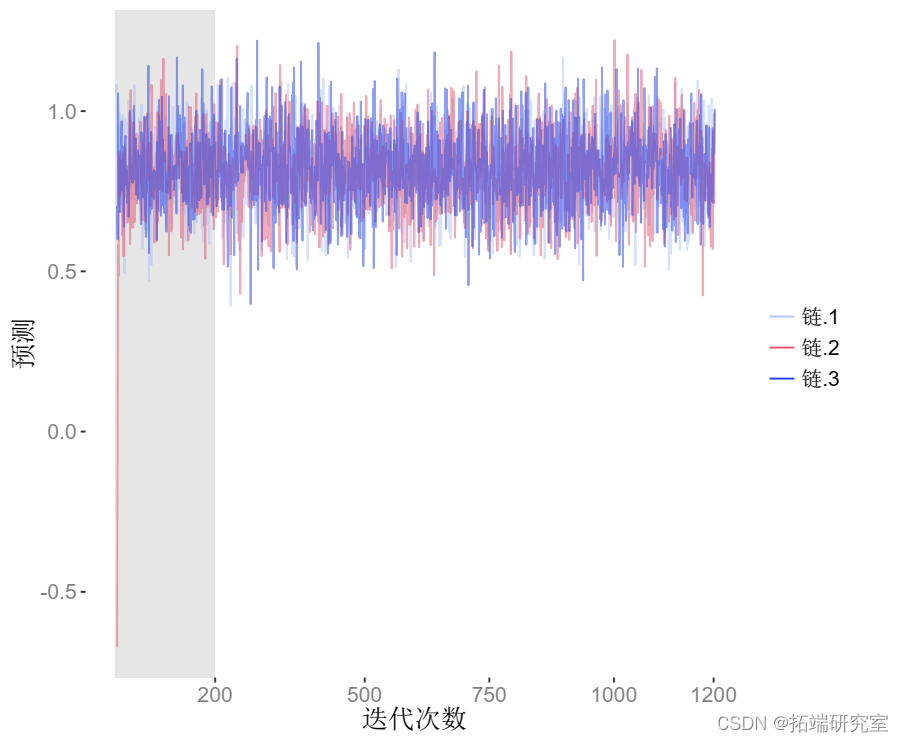
我们可以看到跟踪图中，每条链的估计值都能很快地从起点找到一个或多或少的稳定状态（灰色的初始预烧迭代）。
此外，所有三条链（每条链都用不同的颜色表示）都混合得很好，并在同一结论附近跳动。
stan开发团队通过shinystan包使交互式探索诊断变得很容易。此外，coda包中还有其他诊断方法，Stan模型的结果可以很容易地转换为与之配合。下面的代码演示了如何开始。
bets = extract$beta
所以，你已经有了。除了制作数据列表和产生特定语言的模型代码的初始设置之外，相对于标准模型，运行贝叶斯回归模型并不一定需要太多的时间。最主要的也许是采用不同的思维方式，并从这个新的角度来解释结果。对于你所熟悉的标准模型，可能不需要太长的时间就能像使用那些模型一样自如，现在你将有一个灵活的工具，带你进入新的领域，加深理解。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB贝叶斯优化混合Bayes-CNN-RNN分析股票市场数据与浅层网络超参数优化
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
R语言基于贝叶斯分层、层次Hierarchical Bayesian模型的房价数据空间分析
