
执行多项式回归使用age预测wage。
使用交叉验证为多项式选择最佳次数。选择了什么程度,这与使用ANOVA进行假设检验的结果相比如何?对所得多项式拟合数据进行绘图。
可下载资源
加载工资数据集。保留所有交叉验证误差的数组。我们执行K=10 K倍交叉验证。
rm(list = ls())
set.seed(1)
library(ISLR)
library(boot)
# 测试误差
cv.MSE <- NA
# 循环
for (i in 1:15) {
glm.fit <- glm(wage ~ poly(age, i), data = Wage)
# 交叉验证
cv.MSE[i] <- cv.glm(Wage, glm.fit, K = 10)$delta[1]
}
# 查看结果
cv.MSE## [1] 1675.837 1601.012 1598.801 1594.217 1594.625 1594.888 1595.500
## [8] 1595.436 1596.335 1595.835 1595.970 1597.971 1598.713 1599.253
## [15] 1595.332我们通过绘制type = "b"点与线之间的关系图来说明结果。
在实际应用中,我们常常对总体进行某种分布的假设,抽样得到样本信息,去估计总体参数,这种方法称为参数估计方法。但当对总体信息一无所知,或不假定总体分布形式,只通过样本信息对总体参数进行估计,此时,非参数估计就展现了很强的灵活性。
非参数回归分为局部回归、光滑样条回归、正交回归。光滑样条回归,因其在抽取样本对总体进行回归时,不必依赖总体分布形式,在减小误差、提高预测精确度、提高拟合曲线的光滑度上都体现了良好的特性。
非参数回归模型的一般形式及模型
设Y为因变量 X1,X2,⋯,Xp 为自变量,非参数回归模型的一般形式为
Y=η(X1,X2,⋯,Xp)+ε
其中对p元回归函数只作一些连续性或光滑性的要求。由于非参数回归模型不假定回归函的具体形式而增加了模型的灵活性和适应性。
设 (yi,xi) Math_12#为来自总体 (Y,X) 的一个样本容量为n的独立同分布的样本,需要基于观测值 (yi,xi) Math_15#估计 η(x) 并进行有关的统计推断。
非参数回归的模型为:
E(Y|X=x)=g(X)
数据和模型是统计分析的两个信息来源,数据带有“噪声”,但无偏,而模型实际上是种约束,有助于降低噪声,是响应的。在“偏差–方差”的平衡表上,代表两个极值的分别是标准参数模型和无约束非参数模型。在两个极值之间,存在着大量的非参数或半参数模型,其中大多数被称为平滑方法。非参数估计族可通过惩罚似然法导出各种随机环境下的模型。
三次平滑模型样条
光滑样条回归实际上是一种局部建模方法,是按照一定的光滑性连接起来的分段多项式。首先先介绍多项式样条回归估计,多项式样条估计的最小化式为:
s(f)=∑i=1T(Yi−η(Xi))
在实际生活中,三阶样条比较常用,原理如下:
设某区间 [a,b] 上有实数 t1,t2,⋯,tn 且满足 a<t1<t2<⋯<tn<b , f(x) 是定义在区间 [a,b] 的函数,如 f(x) 满足以下条件[儿童参考]:
1) 在 [a,t1],(t1,t2],⋯,(tn,b] 上,函数 f(x) 为三次多项式。
2) 函数 f(x) 及其二阶导数在 ti(i=1,2,⋯,n) 处处连续。
则称这样的分段多项式函数为三次样条函数, ti 为样条函数的节点。令 t0=a,tn+1=b ,
η(x)=di(x−ti)3+ci(x−ti)2+bi(x−ti)+ai , ti<x<ti+1
为三次光滑样条的表达式。光滑样条估计的基本思想是寻找一个光滑函数使得残差平方和最小,所以引入惩罚函数,使得惩罚平方和最小,估计方法为惩罚最小二乘估计,表达式为:
mins(f)=∑i=1T{yi−η(xi)}2+λ∫ab{η′′(x)}2dx
损失函数 ∑i=1T{yi−η(xi)}2 是使 η 能很好的拟合数据,而 λ∫ab{η′′(x)}2dx 则对函数 η 的波动性进行惩罚,二
阶导数 η′′(x) 对应了斜率的变化程度,衡量的是函数的粗糙度。 λ 为需要选择的光滑参数也称拉格朗日乘子,此方法可以避免多项式样条估计的节点选择对非参数拟合曲线的光滑程度影响。 λ 值越大,函数 η 越光滑。
1) 目标函数均方误差最小
mins(f)=∑i=1T{yi−η(xi)}2+λ∫ab{η′′(x)}2dx
2) 写成矩阵形式,其中 η(x)=∑Nj=1Nj(x)θj
s(θ,λ)=(y−Nθ)T(y−Nθ)+λθTΩNθ
其中 {N}ij=Nj(xi) , {ΩN}ij=∫N′′jN′′kdt 。
3) 运用最小二乘法估计
θˆ=(NTN+λΩN)−1NTy
4) 带入拟合函数
ηˆ=∑Nj=1Nj(x)θˆj
设B为N*M的矩阵,
ηˆ=B(BTB)−1BTy=Hy
5) 求光滑参数 λ
dfλ=trace(Sλ)
Sλ=N(NTN+λΩN)NT=N(NT[I+λN−TΩNN−1]N)−1NT=(I+λN−TΩNN−1)−1
矩阵 Sλ 可以写成 Sλ=(I−λK)−1
此时 mins(η)=(y−η)T(y−η)+ληTKη→ηˆ=Sλy
矩阵S具有对称半定性质,对其进行特征分解:
Sλ=∑Nk=1ρk(λ)ukuTK
其中, ρk(λ)=11+λdk ,这里的 dk 是矩阵K的特征值
6) 估计样条函数
ηˆ=Sλy=∑Nk=1ρk(λ)ukuTKy
# 可视化误差结果
plot( x = 1:15, y = cv.MSE, xlab = "power of age", ylab = "CV error",
type = "b", pch = 19, lwd = 2, bty = "n",
ylim = c( min(cv.MSE) - sd(cv.MSE), max(cv.MSE) + sd(cv.MSE) ) )
#
abline(h = min(cv.MSE) + sd(cv.MSE) , lty = "dotted")
# 误差最小点
points( x = which.min(cv.MSE), y = min(cv.MSE), col = "red", pch = "X", cex = 1.5 )我们再次以较高的年龄权重对模型进行拟合以进行方差分析。
## Analysis of Deviance Table
##
## Model 1: wage ~ poly(age, a)
## Model 2: wage ~ poly(age, a)
## Model 3: wage ~ poly(age, a)
## Model 4: wage ~ poly(age, a)
## Model 5: wage ~ poly(age, a)
## Model 6: wage ~ poly(age, a)
## Model 7: wage ~ poly(age, a)
## Model 8: wage ~ poly(age, a)
## Model 9: wage ~ poly(age, a)
## Model 10: wage ~ poly(age, a)
## Model 11: wage ~ poly(age, a)
## Model 12: wage ~ poly(age, a)
## Model 13: wage ~ poly(age, a)
## Model 14: wage ~ poly(age, a)
## Model 15: wage ~ poly(age, a)
## Resid. Df Resid. Dev Df Deviance F Pr(>F)
## 1 2998 5022216
## 2 2997 4793430 1 228786 143.5637 < 2.2e-16 ***
## 3 2996 4777674 1 15756 9.8867 0.001681 **
## 4 2995 4771604 1 6070 3.8090 0.051070 .
## 5 2994 4770322 1 1283 0.8048 0.369731
## 6 2993 4766389 1 3932 2.4675 0.116329
## 7 2992 4763834 1 2555 1.6034 0.205515
## 8 2991 4763707 1 127 0.0795 0.778016
## 9 2990 4756703 1 7004 4.3952 0.036124 *
## 10 2989 4756701 1 3 0.0017 0.967552
## 11 2988 4756597 1 103 0.0648 0.799144
## 12 2987 4756591 1 7 0.0043 0.947923
## 13 2986 4756401 1 190 0.1189 0.730224
## 14 2985 4756158 1 243 0.1522 0.696488
## 15 2984 4755364 1 795 0.4986 0.480151
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1根据F检验,我们应该选择年龄提高到3次的模型,通过交叉验证 。
现在,我们绘制多项式拟合的结果。
plot(wage ~ age, data = Wage, col = "darkgrey", bty = "n")
...- 拟合step函数以
wage使用进行预测age。绘制获得的拟合图。
cv.error <- NA
...
# 突出显示最小值
points( x = which.min(cv.error), y = min(cv.error, na.rm = TRUE),交叉验证表明,在k = 8的情况下,测试误差最小。最小值的1sd之内的最简约模型具有k = 4,因此将数据分为5个不同的区域。

lm.fit <- glm(wage ~ cut(age, 4), data = Wage)
...
matlines(age.grid, cbind( lm.pred$fit + 2* lm.pred$se.fit,
lm.pred$fit - 2* lm.pred$se.fit),
col = "red", lty ="dashed")该Wage数据集包含了一些其他的变量,如婚姻状况(maritl),工作级别(jobclass),等等。探索其中一些其他预测变量与的关系wage,并使用非线性拟合技术将模型拟合到数据中。
...
summary(Wage[, c("maritl", "jobclass")] )## maritl jobclass
## 1. Never Married: 648 1. Industrial :1544
## 2. Married :2074 2. Information:1456
## 3. Widowed : 19
## 4. Divorced : 204
## 5. Separated : 55# 关系箱线图
par(mfrow=c(1,2))
plot(Wage$maritl, Wage$wage, frame.plot = "FALSE")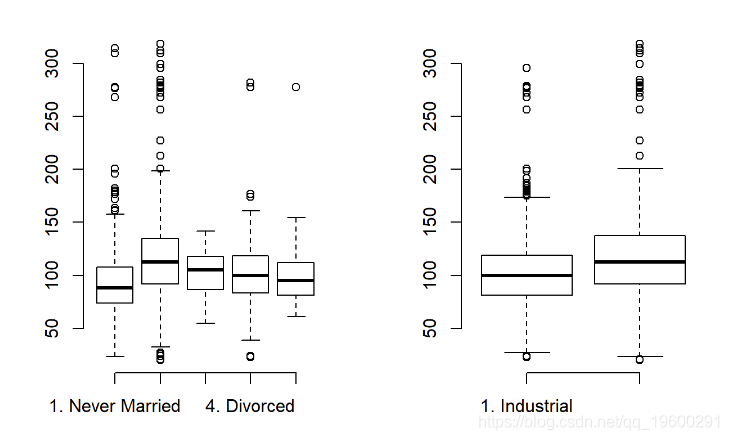
看来一对已婚夫妇平均比其他群体挣更多的钱。信息类工作的工资平均高于工业类工作。
多项式和step函数
m1 <- lm(wage ~ maritl, data = Wage)
deviance(m1) # fit (RSS in linear; -2*logLik)## [1] 4858941m2 <- lm(wage ~ jobclass, data = Wage)
deviance(m2)## [1] 4998547m3 <- lm(wage ~ maritl + jobclass, data = Wage)
deviance(m3)## [1] 4654752正如预期的那样,使用最复杂的模型可以使样本内数据拟合最小化。
我们不能使样条曲线拟合分类变量。
我们不能将样条曲线拟合到因子,但可以使用一个样条曲线拟合一个连续变量并添加其他预测变量的模型。
library(gam)
m4 <- gam(...)
deviance(m4)## [1] 4476501anova(m1, m2, m3, m4)
## Analysis of Variance Table
##
## Model 1: wage ~ maritl
## Model 2: wage ~ jobclass
## Model 3: wage ~ maritl + jobclass
## Model 4: wage ~ maritl + jobclass + s(age, 4)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2995 4858941
## 2 2998 4998547 -3.0000 -139606 31.082 < 2.2e-16 ***
## 3 2994 4654752 4.0000 343795 57.408 < 2.2e-16 ***
## 4 2990 4476501 4.0002 178252 29.764 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1F检验表明,我们从模型四到模型一统计显著改善的变量有年龄,wage,maritl,和jobclass。
Boston数据回归
这个问题使用的变量dis(到五个波士顿就业中心的距离的加权平均值)和nox(每百万人口中一氧化氮的浓度,单位为百万)。我们将dis作为预测变量,将nox作为因变量。
随时关注您喜欢的主题
rm(list = ls())
set.seed(1)
library(MASS)
attach(Boston)## The following objects are masked from Boston (pos = 14):
##
## age, black, chas, crim, dis, indus, lstat, medv, nox, ptratio,
## rad, rm, tax, zn使用poly()函数拟合三次多项式回归来预测nox使用dis。报告回归输出,并绘制结果数据和多项式拟合。
m1 <- lm(nox ~ poly(dis, 3))
summary(m1)##
## Call:
## lm(formula = nox ~ poly(dis, 3))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.121130 -0.040619 -0.009738 0.023385 0.194904
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.554695 0.002759 201.021 < 2e-16 ***
## poly(dis, 3)1 -2.003096 0.062071 -32.271 < 2e-16 ***
## poly(dis, 3)2 0.856330 0.062071 13.796 < 2e-16 ***
## poly(dis, 3)3 -0.318049 0.062071 -5.124 4.27e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.06207 on 502 degrees of freedom
## Multiple R-squared: 0.7148, Adjusted R-squared: 0.7131
## F-statistic: 419.3 on 3 and 502 DF, p-value: < 2.2e-16dislim <- range(dis)
...
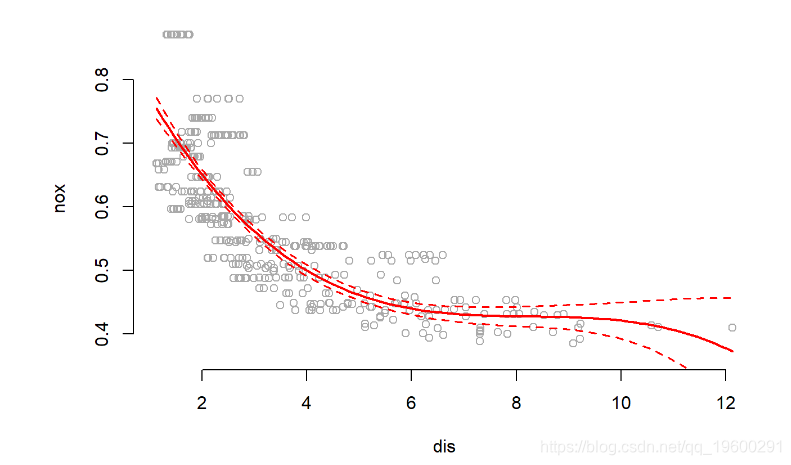
lines(x = dis.grid, y = lm.pred$fit, col = "red", lwd = 2)
matlines(x = dis.grid, y = cbind(lm.pred$fit + 2* lm.pred$se.fit,
lm.pred$fit - 2* lm.pred$se.fit)
, col = "red", lwd = 1.5, lty = "dashed")摘要显示,在nox使用进行预测时,所有多项式项都是有效的dis。该图显示了一条平滑的曲线,很好地拟合了数据。
- 绘制多项式适合不同多项式次数的范围(例如,从1到10),并报告相关的残差平方和。
我们绘制1到10度的多项式并保存RSS。
train.rss <- NA
...
# 训练集模型拟合
train.rss## [1] 2.768563 2.035262 1.934107 1.932981 1.915290 1.878257 1.849484
## [8] 1.835630 1.833331 1.832171正如预期的那样,RSS随多项式次数单调递减。
- 执行交叉验证或其他方法来选择多项式的最佳次数,并解释您的结果。
我们执行LLOCV并手工编码:
#交叉验证误差
cv.error <- matrix(NA, nrow = nrow(Boston), ncol = 10)
...
names(result) <- paste( "^", 1:10, sep= "" )
result## ^1 ^2 ^3 ^4 ^5 ^6
## 0.005471468 0.004022257 0.003822345 0.003820121 0.003785158 0.003711971
## ^7 ^8 ^9 ^10
## 0.003655106 0.003627727 0.003623183 0.003620892plot(result ~ seq(1,10), type = "b", pch = 19, bty = "n", xlab = "powers of dist to empl. center",
ylab = "cv error")
abline(h = min(cv.error) + sd(cv.error), col = "red", lty = "dashed")
基于交叉验证,我们将选择dis平方。
- 使用
bs()函数拟合回归样条曲线使用nox进行预测dis。
我们以[3,6,9]大致相等的4个区间划分此范围
library(splines)
m4 <- lm(nox ~ bs(dis, knots = c(3, 6, 9)))
summary(m4)##
## Call:
## lm(formula = nox ~ bs(dis, knots = c(3, 6, 9)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.132134 -0.039466 -0.009042 0.025344 0.187258
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.709144 0.016099 44.049 < 2e-16 ***
## bs(dis, knots = c(3, 6, 9))1 0.006631 0.025467 0.260 0.795
## bs(dis, knots = c(3, 6, 9))2 -0.258296 0.017759 -14.544 < 2e-16 ***
## bs(dis, knots = c(3, 6, 9))3 -0.233326 0.027248 -8.563 < 2e-16 ***
## bs(dis, knots = c(3, 6, 9))4 -0.336530 0.032140 -10.471 < 2e-16 ***
## bs(dis, knots = c(3, 6, 9))5 -0.269575 0.058799 -4.585 5.75e-06 ***
## bs(dis, knots = c(3, 6, 9))6 -0.303386 0.062631 -4.844 1.70e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0612 on 499 degrees of freedom
## Multiple R-squared: 0.7244, Adjusted R-squared: 0.7211
## F-statistic: 218.6 on 6 and 499 DF, p-value: < 2.2e-16# 绘图结果
...
#
matlines( dis.grid,
...
col = "black", lwd = 2, lty = c("solid", "dashed", "dashed"))
- 现在针对一定范围的自由度拟合样条回归,并绘制结果拟合并报告结果RSS。描述获得的结果。
box <- NA
for (i in 3:16) {
...
}
box[-c(1, 2)]## [1] 1.934107 1.922775 1.840173 1.833966 1.829884 1.816995 1.825653
## [8] 1.792535 1.796992 1.788999 1.782350 1.781838 1.782798 1.783546ISLR包中的College数据集。
我们使用3到16之间的dfs拟合回归样条曲线。
- 将数据分为训练集和测试集。使用学费作为因变量,使用其他变量作为预测变量,对训练集执行前向逐步选择,确定仅使用预测变量子集的令人满意的模型。
rm(list = ls())
set.seed(1)
library(leaps)
attach(College)## The following objects are masked from College (pos = 14):
##
## Accept, Apps, Books, Enroll, Expend, F.Undergrad, Grad.Rate,
## Outstate, P.Undergrad, perc.alumni, Personal, PhD, Private,
## Room.Board, S.F.Ratio, Terminal, Top10perc, Top25perc# 分割测试集训练集
train <- sample( length(Outstate), length(Outstate)/2)
test <- -train
...
abline(h=max.adjr2 - std.adjr2, col="red", lty=2)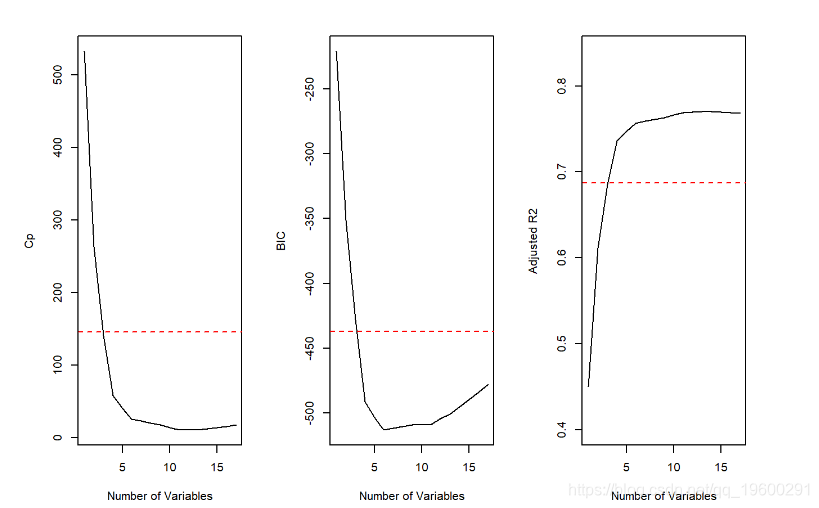
所有cp,BIC和adjr2得分均显示6是该子集的最小大小。但是,根据1个标准误差规则,我们将选择具有4个预测变量的模型。
...
coefi <- coef(m5, id = 4)
names(coefi)## [1] "(Intercept)" "PrivateYes" "Room.Board" "perc.alumni" "Expend"将GAM拟合到训练数据上,使用学费作为响应,并使用在上一步中选择的函数作为预测变量。绘制结果,并解释您的发现。
library(gam)
...
plot(gam.fit, se=TRUE, col="blue")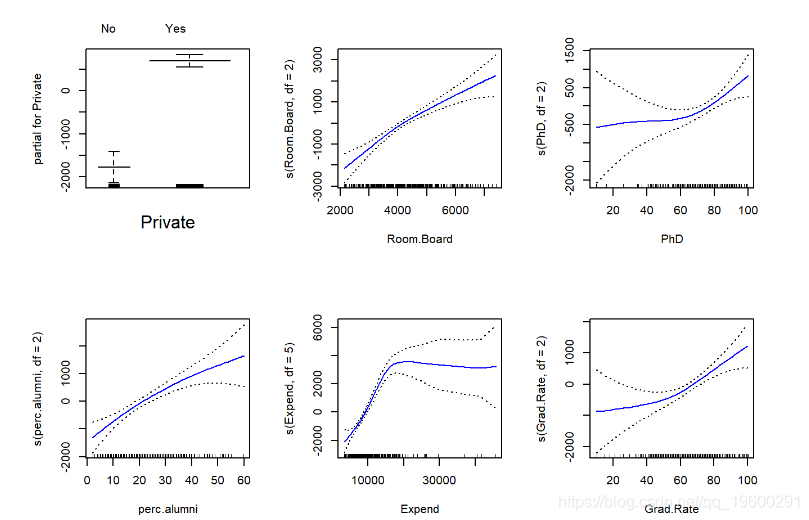
评估在测试集上获得的模型,并解释获得的结果。
gam.pred <- predict(gam.fit, College.test)
gam.err <- mean((College.test$Outstate - gam.pred)^2)
gam.err## [1] 3745460gam.tss <- mean((College.test$Outstate - mean(College.test$Outstate))^2)
test.rss <- 1 - gam.err / gam.tss
test.rss## [1] 0.7696916- 对于哪些变量(如果有),是否存在与因变量呈非线性关系的证据?
summary(gam.fit)
##
## Call: gam(formula = Outstate ~ Private + s(Room.Board, df = 2) + s(PhD,
## df = 2) + s(perc.alumni, df = 2) + s(Expend, df = 5) + s(Grad.Rate,
## df = 2), data = College.train)
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4977.74 -1184.52 58.33 1220.04 7688.30
##
## (Dispersion Parameter for gaussian family taken to be 3300711)
##
## Null Deviance: 6221998532 on 387 degrees of freedom
## Residual Deviance: 1231165118 on 373 degrees of freedom
## AIC: 6941.542
##
## Number of Local Scoring Iterations: 2
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq F value Pr(>F)
## Private 1 1779433688 1779433688 539.106 < 2.2e-16 ***
## s(Room.Board, df = 2) 1 1221825562 1221825562 370.171 < 2.2e-16 ***
## s(PhD, df = 2) 1 382472137 382472137 115.876 < 2.2e-16 ***
## s(perc.alumni, df = 2) 1 328493313 328493313 99.522 < 2.2e-16 ***
## s(Expend, df = 5) 1 416585875 416585875 126.211 < 2.2e-16 ***
## s(Grad.Rate, df = 2) 1 55284580 55284580 16.749 5.232e-05 ***
## Residuals 373 1231165118 3300711
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Anova for Nonparametric Effects
## Npar Df Npar F Pr(F)
## (Intercept)
## Private
## s(Room.Board, df = 2) 1 3.5562 0.06010 .
## s(PhD, df = 2) 1 4.3421 0.03786 *
## s(perc.alumni, df = 2) 1 1.9158 0.16715
## s(Expend, df = 5) 4 16.8636 1.016e-12 ***
## s(Grad.Rate, df = 2) 1 3.7208 0.05450 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1非参数Anova检验显示了因变量与支出之间存在非线性关系的有力证据,以及因变量与Grad.Rate或PhD之间具有中等强度的非线性关系(使用p值为0.05)。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析




1 comment on “R语言ISLR工资数据进行多项式回归和样条回归分析”