我们研究波动聚集,以及使用单变量 GARCH(1,1) 模型对其进行建模。
我们研究波动聚集,以及使用单变量 GARCH(1,1) 模型对其进行建模。
波动聚集
波动聚集——存在相对平稳时期和高波动时期的现象——是市场数据的一个看似普遍的属性。对此没有普遍接受的解释。
GARCH(广义自回归条件异方差)模型 波动聚集。图 1 是波动率的 garch 模型的示例。
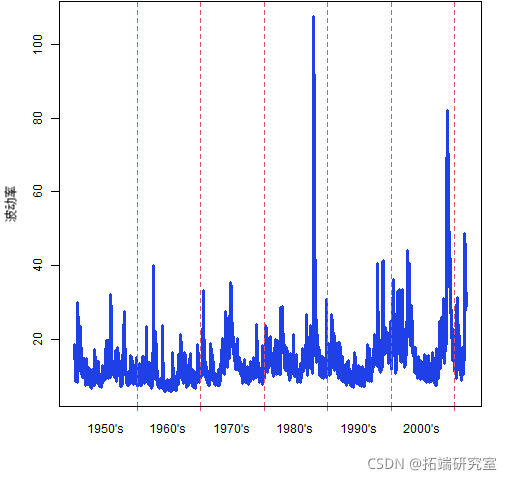
图 1:根据 garch(1,1) 模型估计的 2011 年底之前的标准普尔 500 指数波动率
可下载资源
显然,波动性随时间变化。图 1 是波动率模型,而不是真正的波动率。但如果我们有一张真实波动率的图片,它看起来会非常像图 1。
数据需求
提供给 garch 估计的数据是每日数据。你可以使用每周或每月的数据,但这将使数据中的一些波动变得平滑。
你可以用garch处理日内数据,但这变得很复杂。 一天中的波动有季节性。 季节性在很大程度上取决于交易发生的特定市场,也可能取决于特定资产。 一个例子是看盘中的风险值。
图1没有显示真实的波动性,因为我们从来没有观察过波动性。 波动性曾经只是间接地暴露在我们面前。 所以我们试图估计一些未知的东西。
图 2 是一个原型 garch 模型图。
图 2:“无噪音”garch 模型图
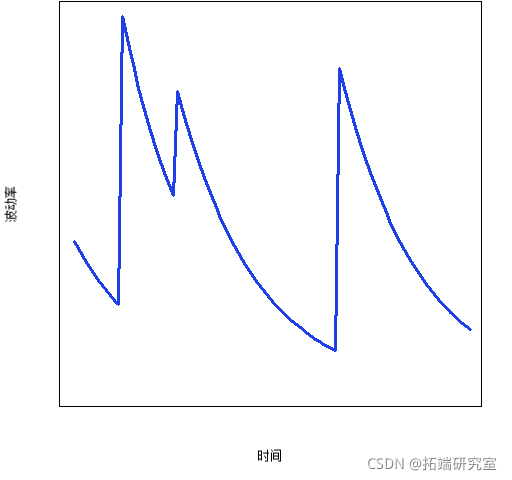
garch 的观点是波动率上升然后衰减,直到出现另一个峰值。很难在图 1 中看到这种行为,因为时间轴太紧凑了,因此在图 3 中更加明显。
图 3:由 garch(1,1) 模型估计的 MMM 波动率。
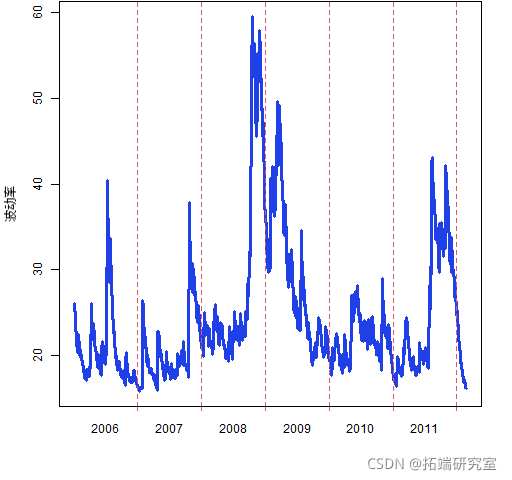
当然,在真实数据中,有各种规模的冲击,而不仅仅是大的冲击。
请注意,来自公告的波动性(与冲击相反)是反过来的–波动性随着公告时间的临近而增加,然后在公告结果出来后消失。
对Garch模型的估计主要是对衰减速度的估计。 它所看到的衰减是非常嘈杂的,所以它希望看到大量的数据。 大量的数据是指它希望有数以万计的每日观测数据。
有两个原因不能给它大量的观测数据。
- 你没有那么多观察数据
- 市场随时间变化
所以有一个折中的方法。每天 2000 次观察往往不无道理。
如果你每天的观测值少于1000个,那么估计就不可能给你提供很多关于参数的真实信息。 最好是选择一个 “合理的 “模型。 这将是一个具有大约正确的持久性的模型(见下文),α1参数在0和0.1之间,β1参数在0.9和1之间。
随时关注您喜欢的主题
估计
我们使用 GARCH(1,1) 模型;不是因为它是最好的,因为它是最常用的。
Garch 模型几乎总是通过最大似然估计。结果证明这是一个非常难的优化问题。假设你有足够重要的数据,即使是最好的 garch 实现也需要关注优化。
我们知道,收益率没有正态分布,它们有长尾。 假设长尾完全是由于arch效应造成的,这是完全合理的,在这种情况下,在arch模型中使用正态分布将是正确的做法。 然而,使用长尾分布的可能性,结果是给出一个更好的拟合(几乎总是如此)。 t分布似乎做得很好。
自相关
如果模型正确解释了波动聚集,则平方标准化残差将不存在自相关。通常进行 Ljung-Box 检验来检验这种自相关性。
下面是假设 MMM 收益率正态分布的拟合输出(在本例中实际上是 Box-Pierce):
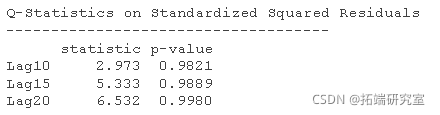
如果你习惯于看拟合度检验的p值,你可能会注意到一些奇怪的东西。 检验表明,我们用4个参数过度拟合了1547个观测值。 我不这么认为。
更好的解释是,尽管检验是非常稳健的,但对这种极端的数据来说,检验并不稳健。 这样检验平方残差可能会产生反作用。 一个有信息量的检验是关于平方标准化残差的行列。
持久性
garch模型的持久性与冲击后大的波动率衰减的速度有关。对于garch(1,1)模型来说,关键的统计数字是两个主要参数(alpha1和beta1,我们在这里使用的符号)的总和。
α1和β1的总和应该小于1。 如果总和等于1,那么我们就有一个指数衰减模型。
可以用半衰期来表示持久性。 半衰期是log(0.5)/log(alpha1 + beta1),其中的单位将是收益率的频率。 当α1+β1达到1时,半衰期就变成了无限。
为什么我们会得到具有无限持久性的估计? 持久性是通过观察在样本期间衰减的速度来估计的。 如果在样本期间波动率有一个趋势,那么估计者就会 “认为 “它从未看到完全的衰减。 样本期越短,越有可能出现欺骗估计的趋势。
无论参数估计值是多少,波动率的样本内估计值看起来都很相似。 如果我们改变各自模型的参数估计值,图 1 和图 3 不会有太大变化。 但是当我们在样本外进行预测时,参数就很重要了。
使用Garch
Garch 模型之所以有用,是因为以下两点:
- 你可以使用 garch 模型进行预测
- 你可以使用 garch 模型进行模拟
预测
你预测的越远,你的模型就越接近完美。Garch 模型并不是特别接近完美。如果你在一个月或更长时间的时间范围内进行预测,那么效果可能不好。 如果你预测的是未来几天,那么Garch应该是相当有用的。
模型的持久性是预测的关键驱动因素——它决定了预测进入无条件波动的速度。如果波动率确实存在很多持久性,并且你的模型准确地捕捉到了这种持久性,那么你将在很远的地方获得良好的预测。
有两种不同的事情可以预测:
- 预测期各时间点的波动率
- 从周期开始到周期中每个时间点的平均波动率
例如,期权价格的波动率是到期前的平均波动率,而不是到期日的波动率。
因此,在预测时你需要了解两件事:
- 你想要哪个预测
- 你得到哪个预测
模拟
garch 模拟需要:
- garch 模型(包括参数值)
- 模型的波动状态
- 标准化(方差 1)的分布
我们想要的波动状态几乎总是数据末尾的状态。我们想利用当前的波动状态并展望未来。
使用经验分布——拟合模型的标准化残差——通常是分布的最佳选择。即使在使用经验分布时,拟合模型时的分布假设也会产生影响。
估计程序“试图”使残差符合假设的分布。假设正态分布的模型的标准化残差将比假设分布相同数据的模型的残差更接近正态分布。
模拟依赖于估计的参数,但不像预测那样严重。 当我们模拟到更远的未来时,模型误差会加重。
R包
R 中的 garch 建模有多种选择。没有一种是完美的,使用哪种可能取决于你想要实现的目标。然而,rugarch 对于许多人来说, 它可能是最好的选择。
rugarch
这具有拟合(即估计参数)、预测和模拟的功能。
以下是使用 Student t 分布进行拟合的示例:
ugarchspec(mean.modl, distriuion) ugarchfit(ru, ret) coef
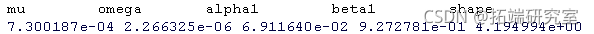
> # 绘制样本内波动率估计值 > plot(sqrt(252) * sigma)
这个包中的优化可能是我讨论的包中最复杂和最值得信赖的。
fGarch
我们将拟合与上述相同的 Student t 模型:
garchFit(sp5, cod.dit="std") coef

> # 绘制样本内波动率估计值 > plot(sqrt(252) * gfit.fg@sigma.t, type="l")
tseries
这个包是第一个在 R 中包含公开可用的 garch 函数的包。它仅限于正态分布。
garch(sp5) coef
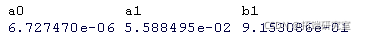
> # 绘制样本内波动率估计值 > plot(sqrt(252) *fittedalus)
bayesGARCH
对Garch模型进行贝叶斯估计。
这个包所做的唯一模型是具有t分布误差的garch(1,1)。
bayesGARCH(sp5)
但是,此命令失败并出现错误。如果我们以百分比形式给出收益率,则该命令确实有效:
bayesGARCH(sp5 * 100)
这也可能是最大似然估计的一个问题。 至少有一个Garch的实现在优化百分比收益而不是自然比例的收益方面要好得多。 你可以对优化做一个测试,就是在两种规模的收益率上估计模型并比较结果。
不过,bayesGARCH函数并没有给我们一个估计值。 它给我们的是一个矩阵,列对应于参数,行对应于马尔科夫链蒙特卡洛。 这可以说是参数的(后验)分布的一个样本。
如果我们对持久性施加一个约束,我们可以得到一个更有用的分析。 我们通过为约束条件创建一个函数来做到这一点。
pi\[2\] + pi\[3\] < .9986
这就是说超过两年的半衰期是不合理的。然后我们使用该约束:
cotrl=list(adPrrdos=prieces))
现在我们从结果中进行选择并计算分布中的半衰期:
然后绘制结果。
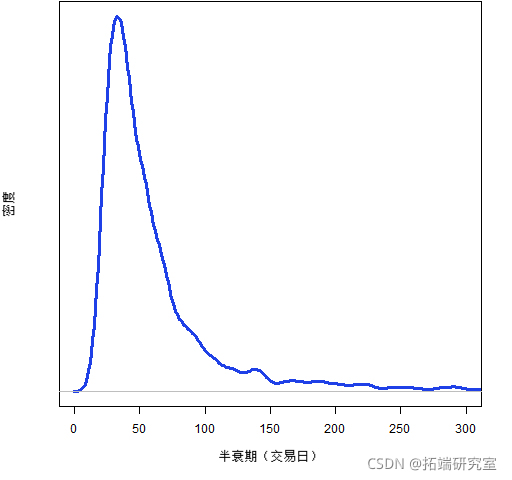
图 3:MMM 波动率半衰期的贝叶斯估计
betategarch
该包拟合具有 t 分布误差的 EGARCH 模型。
tegarch.est(sp5) par

tegarch.fit(sp5, par) plot(sqrt(252) * siga * sd(epiln\]))
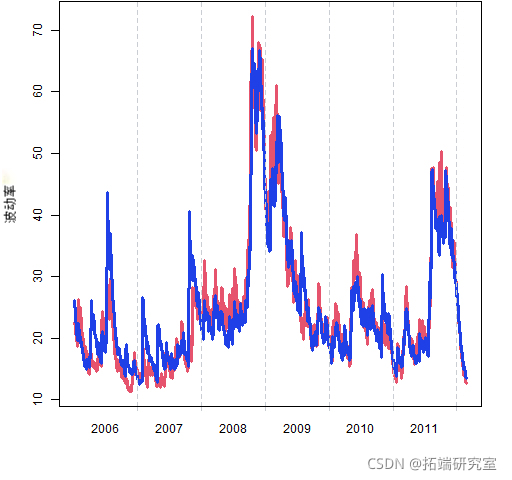
图 4 将这个估计值与 garch(1,1)估计值进行了比较(来自 rugarch,但它们看起来都非常相似)。
图 4: 由 garch(1,1) 模型(蓝色)和 beta-t EGARCH 模型(红色)估计的 MMM 波动率
dynamo
我认为在这个包中估计一个 garch 模型的方法是:
dm(sp~ garch(1,1))
AutoSEARCH
该包将为 ARCH 模型选择最佳滞后。
rugarch 包中的 garch 模型
如何拟合和使用garch 模型。
模型
这模型通常比更常见的 garch(1,1) 模型效果更好。
图 5 显示了拟合标准普尔 500 指数的两个模型对未来 20 天每天波动率的预测。模型对波动率的预测更为细致。
图 5:使用模型(蓝色)和具有方差目标(红色)的 garch(1,1) 对每天的波动率预测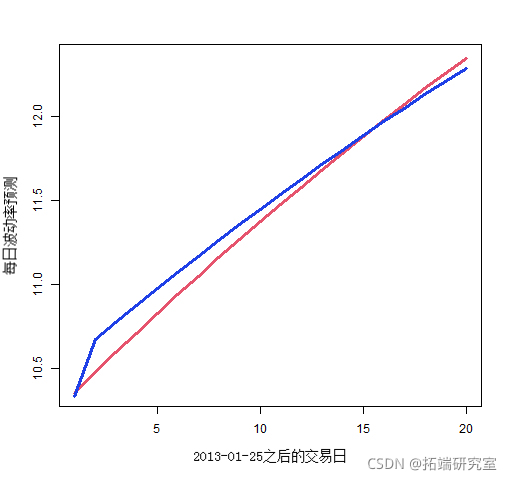
通常,你关心的是从现在到指定日期的平均波动率。这被称为期限结构——图 6 显示了这一点。
图 6:使用分量模型(蓝色)和具有方差目标(红色)的 garch(1,1) 预测标准普尔 500 指数的波动率期限结构
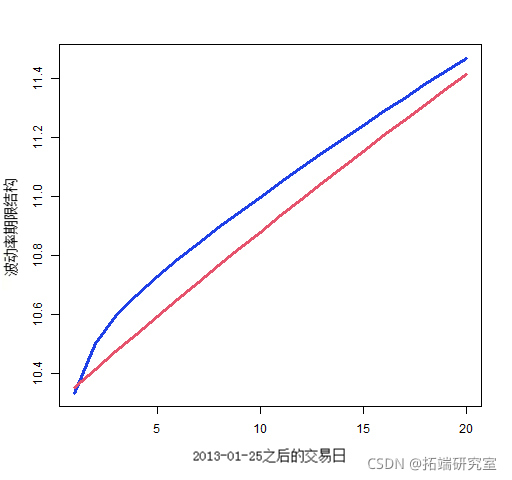
创建这些图的代码如下所示。
R代码
该 rugarch 软件包允许选择拟合模型。
错误
首先这是我遇到的一个问题:
SET\_VECTOR\_ELT() can only be applied to a 'list', not a 'symbol'
更新这些包可以解决问题。
卸载包后,我更新了 Rcpp 和 RcppArmadillo 包。仍然不能正常工作。
再次安装 Rcpp 后,成功了。
模型被调用 "csGARCH" , rugarch 两个额外的参数被称为 eta11 (我的符号中的ρ)和 eta21 (φ)。它的分布和常数平均值是:
ugarchspec(mean.model, ditrbuton, vriane.moel)
用途如下:
Warning message: In .makefitmodel NaNs produced
警告信息似乎是关于:
fit$coH \[1\] NaN
估计系数和半衰期为:
> coef

> halflife

具有方差目标的 garch(1,1) 模型的规范是:
ugarchspec(mean.moel, isrition, varane.moel, vrince.tgtng=TRUE))
预测
一旦模型拟合好,你就可以进行预测。
ugarchforecast()
一旦我们得到了预测的波动率,我们就可以绘制它。生成图5 的函数是:
plot(1:20, spf}
图 6 的函数是:
plot(sqrt(cumsum(spe^2)/(1:20))
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 LangGraphSwarm的银行数据分析群体智能代理:Text-to-SQL、EDA可视化与动态任务编排|附代码数据
LangGraphSwarm的银行数据分析群体智能代理:Text-to-SQL、EDA可视化与动态任务编排|附代码数据 CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据
CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程
Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程



