本文使用波兰公寓价格数据说明Fisher检验。

由Kaizong Ye，Liao Bao撰写

我们先绘制各地区价格的箱线图

with(data = apart , boxplot(price ~ dis ))

可下载资源

完整程序、数据和文档（word）

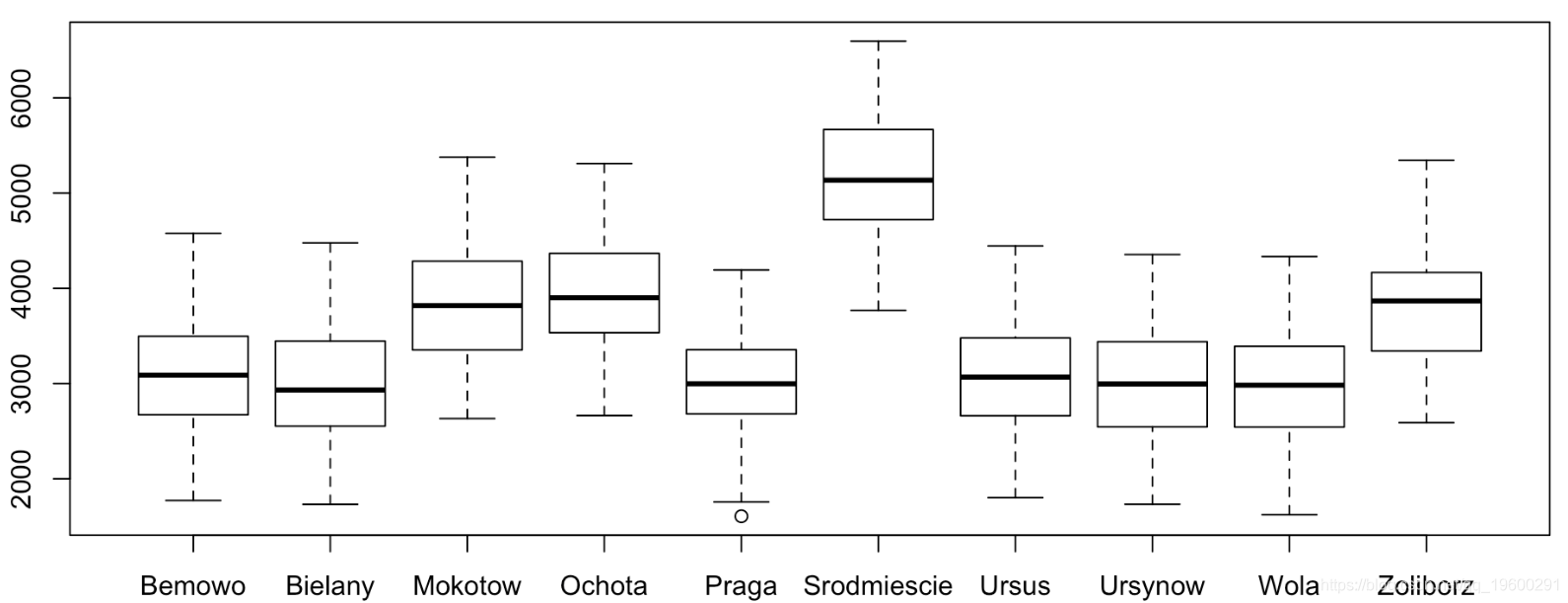
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

问题：（1）对于2*2的列联表，该用哪种检验方法？（2）对于R*C的列联表，该用哪种检验方法？

行×列表卡方检验注意事项

1.一般认为行×列表中不宜有1/5以上格子的理论数小于5，或有小于1的理论数。当理论数太小可采取下列方法处理：

①增加样本含量以增大理论数；

②删去上述理论数太小的行和列；

③将太小理论数所在行或列与性质相近的邻行邻列中的实际数合并，使重新计算的理论数增大。

由于后两法可能会损失信息，损害样本的随机性，不同的合并方式有可能影响推断结论，故不宜作常规方法。另外，不能把不同性质的实际数合并，如研究血型时，不能把不同的血型资料合并。

2.如检验结果拒绝检验假设，只能认为各总体率或总体构成比之间总的来说有差别，但不能说明它们彼此之间都有差别，或某两者间有差别。

总结：

若一个2*2的列联表为：

a b

c d

则n为2*2列联表的总频数（a+b+c+d）。而T为理论频数。对于a，其理论频数为(a+b)*(a+c)/n，即所在行的频数之和*所在列的频数之和/总频数。

主要结论：

一：对于2*2的列联表：

（1）当T（此处为最小理论频数，下同）>=5, n>=40 时，直接用Pearson 卡方检验；

（2）当1 = 40 时，需要用连续性校正公式做卡方检验。这是因为卡方分布为连续型分布，而2*2列联表资料是分类资料，所以样本量较小时要进行连续性校正。

（3）当T<1 , 或者 n < 40, 或做卡方检验后所得的P值接近检验水准a 时，用Fisher exact test

二：对于行×列表资料检验

要求每个格子中的理论频数T均大于5或1<1或1

我们在这里对公寓进行分组（这也可以通过简单的回归，这里5个解释变量并不重要）。我们可以重新排列

A = A[order(A$x),]

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

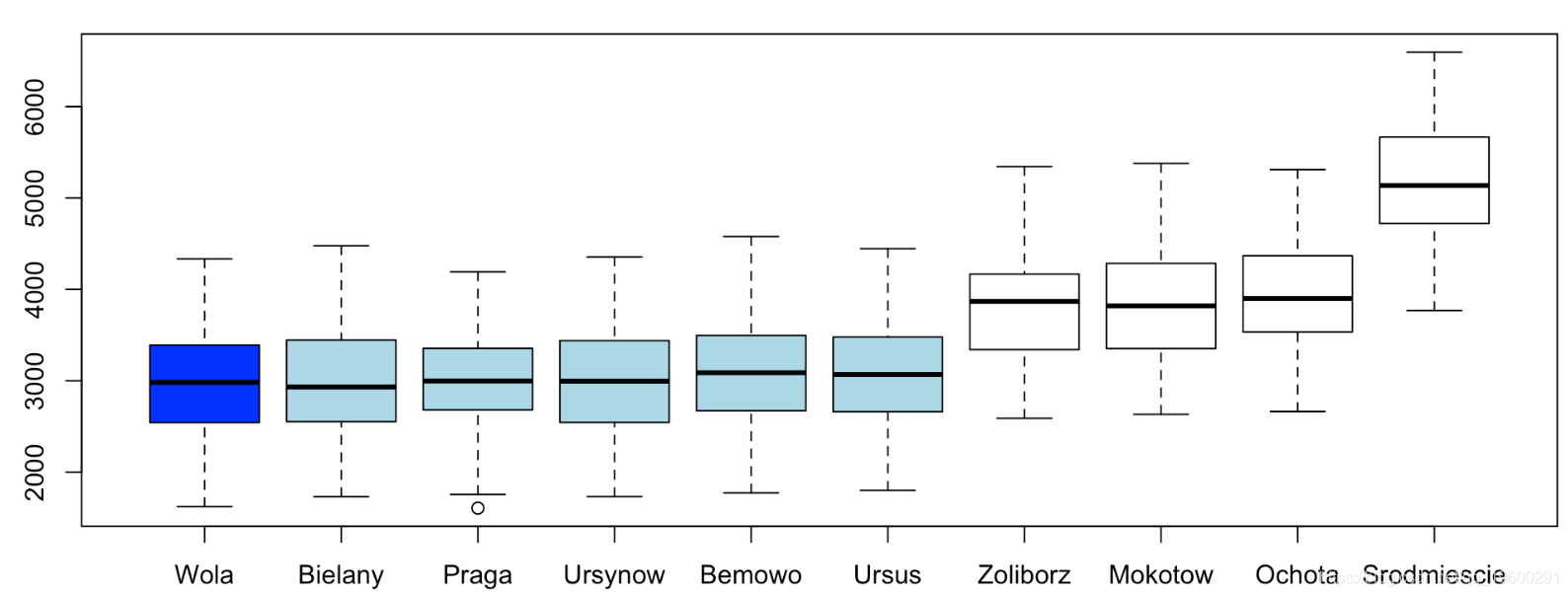
我们以这里最便宜的地区为参考，

 Coefficients:
Estimate Std. Error t value Pr(&gt;|t|) 
(Intercept) 2968.36 58.02 51.160 &lt;2e-16 ***
districtBielany 17.38 84.16 0.207 0.836 
districtPraga 26.45 85.12 0.311 0.756 
districtUrsynow 42.01 82.65 0.508 0.611 
districtBemowo 80.10 83.71 0.957 0.339 
districtUrsus 102.01 82.25 1.240 0.215 
districtZoliborz 829.59 83.94 9.884 &lt;2e-16 ***
districtMokotow 887.10 81.86 10.837 &lt;2e-16 ***
districtOchota 987.93 84.16 11.738 &lt;2e-16 ***
districtSrodmiescie 2214.39 83.28 26.591 &lt;2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 597.4 on 990 degrees of freedom
Multiple R-squared: 0.5698,	Adjusted R-squared: 0.5659 
F-statistic: 145.7 on 9 and 990 DF, p-value: &lt; 2.2e-16

我们可以检验前5个地区价格，这是一个多重检验，我们将使用Fisher检验：

linHypo(reg, c("districtBielany = 0" 
"districtPraga = 0" 
"districtUrsynow = 0" 
"districtBemowo = 0" 
"districtUrsus = 0") 
Linear hypothesis test
 
Model 1: restricted model
Model 2: m2.price ~ district
 
Res.Df RSS Df Sum of Sq F Pr(&gt;F)
1 995 354051715 
2 990 353269202 5 782513 0.4386 0.8217

Fisher的统计数据很低， p值为82％。

Linear hypothesis test
 
Model 1: restricted model
Model 2: m2.price ~ district
 
Res.Df RSS Df Sum of Sq F Pr(&gt;F) 
1 996 405455409 
2 990 353269202 6 52186207 24.374 &lt; 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

我们将对前6种地区进行重组（并称A为地区重组）。如果我们看平均价格，按地区，我们得到

with(data = apar , boxplot( price ~ distr ))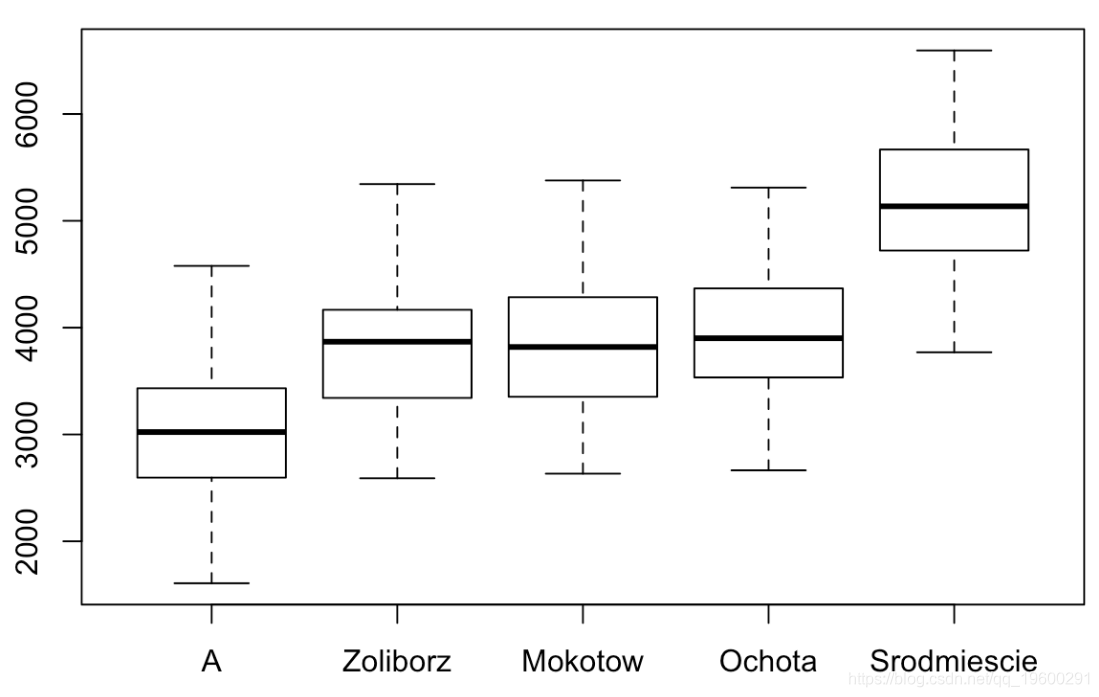

最受欢迎的见解

1.Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV，Stochastic Volatility）模型

2.基于R语言的疾病制图中自适应核密度估计的阈值选择方法

3.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

4.R语言回归中的hosmer-lemeshow拟合优度检验

5.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型估计

6.R语言区间数据回归分析

7.R语言WALD检验 VS 似然比检验

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

我们再次开始，以最便宜的地区作为参考，我们想检验线性回归中接下来的两个地区的系数是否为零。

R语言Wald检验 vs 似然比检验

阅读文章 ➜

 
Linear hypothesis test
 
Model 1: restricted model
Model 2: m2.price ~ district
 
Res.Df RSS Df Sum of Sq F Pr(<F)
1 997 355292524 
2 995 354051715 2 1240809 1.7435 0.1754

P为0.17，我们可以接受原假设。然后，我们有三组地区，名称分别为A，B和C。我们获得以下框线图

with(data = apart , boxplot( price ~ dist ))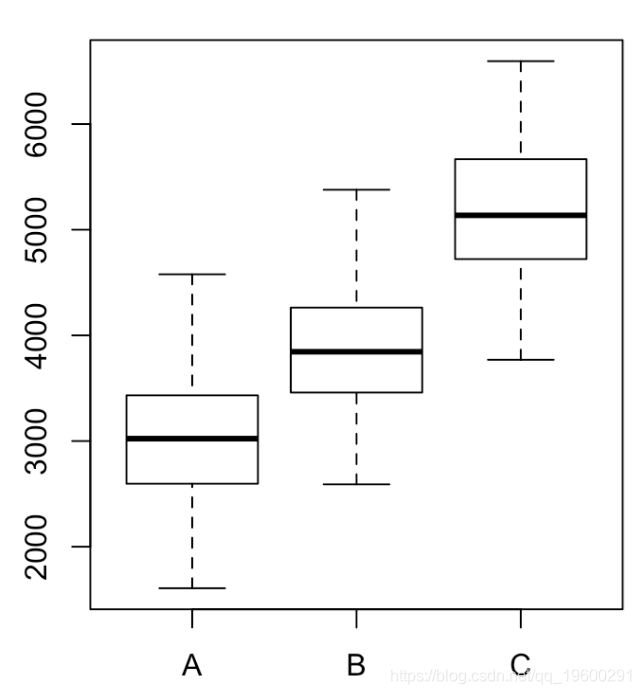

因此，最终我们可以分类成三个不同的地区，如果目标是预测价格，则无需使用10类分类，而3类分类就足够了！

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言Fisher检验探究地区间公寓价格的关系

R语言Wald检验 vs 似然比检验

相关文章

R语言Fisher检验探究地区间公寓价格的关系

R语言Wald检验 vs 似然比检验

相关文章

关注有关新文章的微信公众号