在这个例子中,我们考虑马尔可夫转换随机波动率模型。
设 yt为因变量,xt 为 yt 未观察到的对数波动率。对于 t≤tmax,随机波动率模型定义如下
统计模型
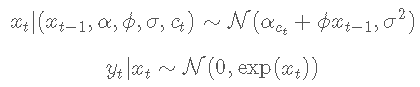
1.序列估计问题
谈起序列蒙特卡洛,就不得不说状态空间模型,可以说序列蒙特卡洛就是为了解决状态空间模型的参数估计问题而生的
状态空间模型指的是一个系统的状态会随着时间发生改变,进而导致这个系统对外展现出的变量也就是观测变量会发生改变。这个系统的状态可以用状态变量表示,观测值可以用观测变量表示。状态变量记为 ,观测变量记为
通常我们对这个系统的问题主要有三个方面:
-
后验概率估计:
-
观测变量的边际似然:
-
某些函数的期望:
2.采样
2.1 序列重要性采样
在上一篇文章中我们讲过,重要性采样给予每个粒子不同的权重,通过加权的方法算出期望、面积等问题
对于状态空间模型,粒子采样的方法通常选用序列重要性采样。采样过程首先从提议分布里对t时刻的变量进行采样,接下来通过上一代的粒子权重与本次计算出的粒子权重相乘计算出序列的权重
提议分布:
粒子权重:
2.2 缺点
序列重要性采样可以计算出对应一整个时间序列的粒子权重,但是这种采样方法可能导致部分粒子序列权重小,而只有少数粒子序列的权重大。从长期来看,这种方法计算出的期望和面积等不稳定,因此我们需要引入重采样机制。
3. 重采样
重采样机制是指对于权重较大的粒子序列进行复制,对于权重较小的粒子序列进行抛弃,通过重采样后,我们获得N个权重相等的粒子序列。通过重采样,我们可以避免之前重要性采样中由于权重迭代次数过多导致部分粒子权重很小,部分粒子权重很大的问题。重采样方法主要有系统重采样、残差重采样、多项式重采样等。为了减少计算量我们同时还引入了自适应重采样机制
重采样的粒子,计算出权重后,对于权重大的粒子予以保留同时复制,抛弃权重小的粒子,用新得到的粒子来拟合分布
状态变量 ct 遵循具有转移概率的二状态马尔可夫过程
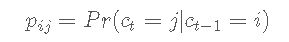
N(m,σ2)表示均值 m 和方差 σ2的正态分布。
BUGS语言统计模型
文件内容 'vol.bug':
dlfie = 'vol.bug' #BUGS模型文件名
设置
设置随机数生成器种子以实现可重复性
set.seed(0)
加载模型和数据
模型参数
dt = lst(t\_mx=t\_mx, sa=sima, alha=alpa, phi=pi, pi=pi, c0=c0, x0=x0)
可下载资源
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
视频
什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
解析编译BUGS模型,以及样本数据
modl(mol\_le, ata,sl\_da=T)

绘制数据
plot(1:tmx, y, tpe='l',xx = 'n')
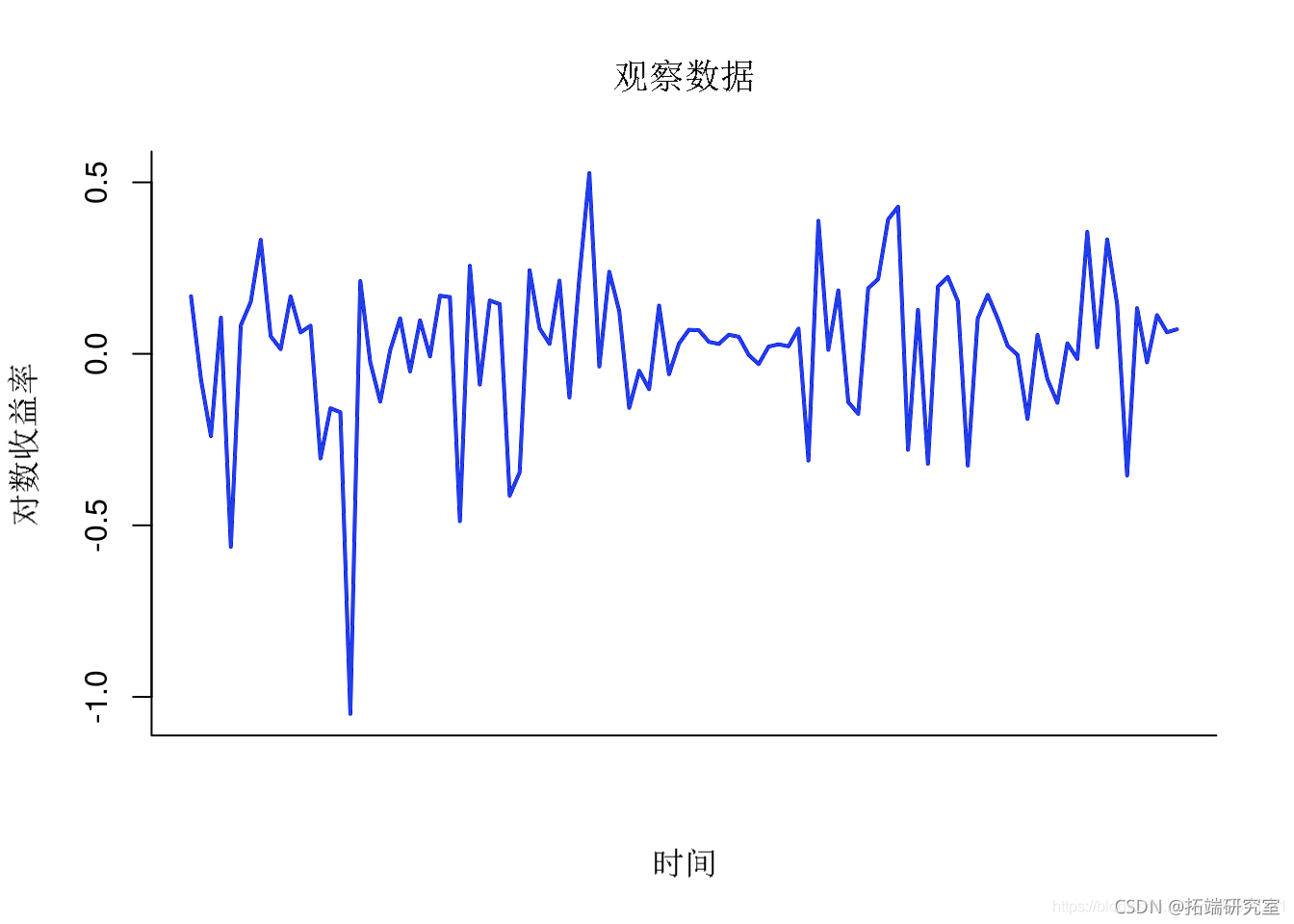
对数收益率
序列蒙特卡罗_Sequential Monte Carlo_
运行
n= 5000 # 粒子的数量
var= c('x') # 要监测的变量
out = smc(moe, vra, n)

模型诊断
diagnosis(out)
绘图平滑 ESS
plt(ess, tpe='l') lins(1:ta, ep(0,tmx))
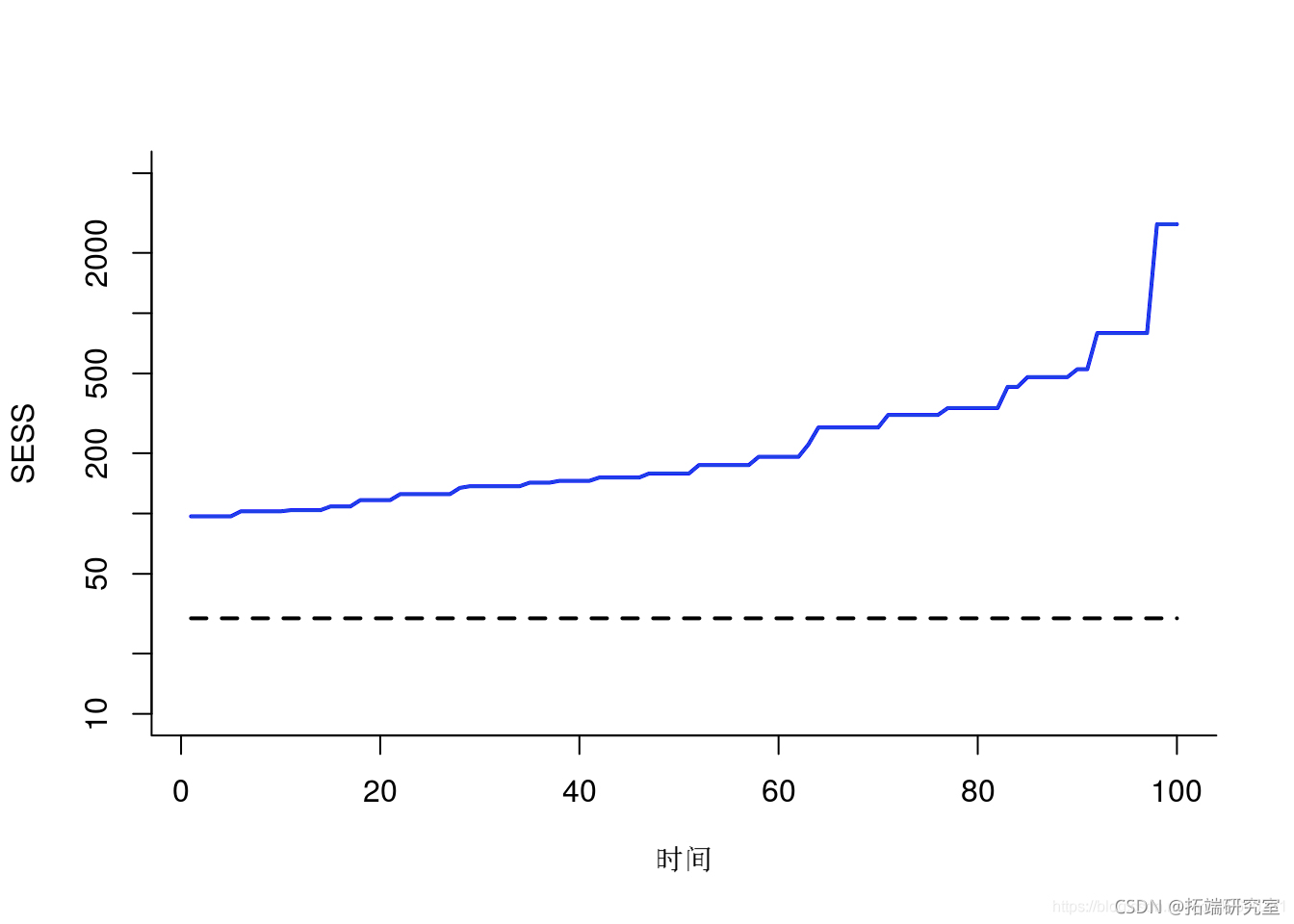
SMC:SESS
绘制加权粒子
plt(1:tax, out,)
for (t in 1:_ax) {
vl = uiq(valest,\])
wit = sply(vl, UN=(x) {
id = utm$$sles\[t,\] == x
rtrn(sm(wiht\[t,ind\]))
})
pints(va)
}
lies(1t_x, at$xue)
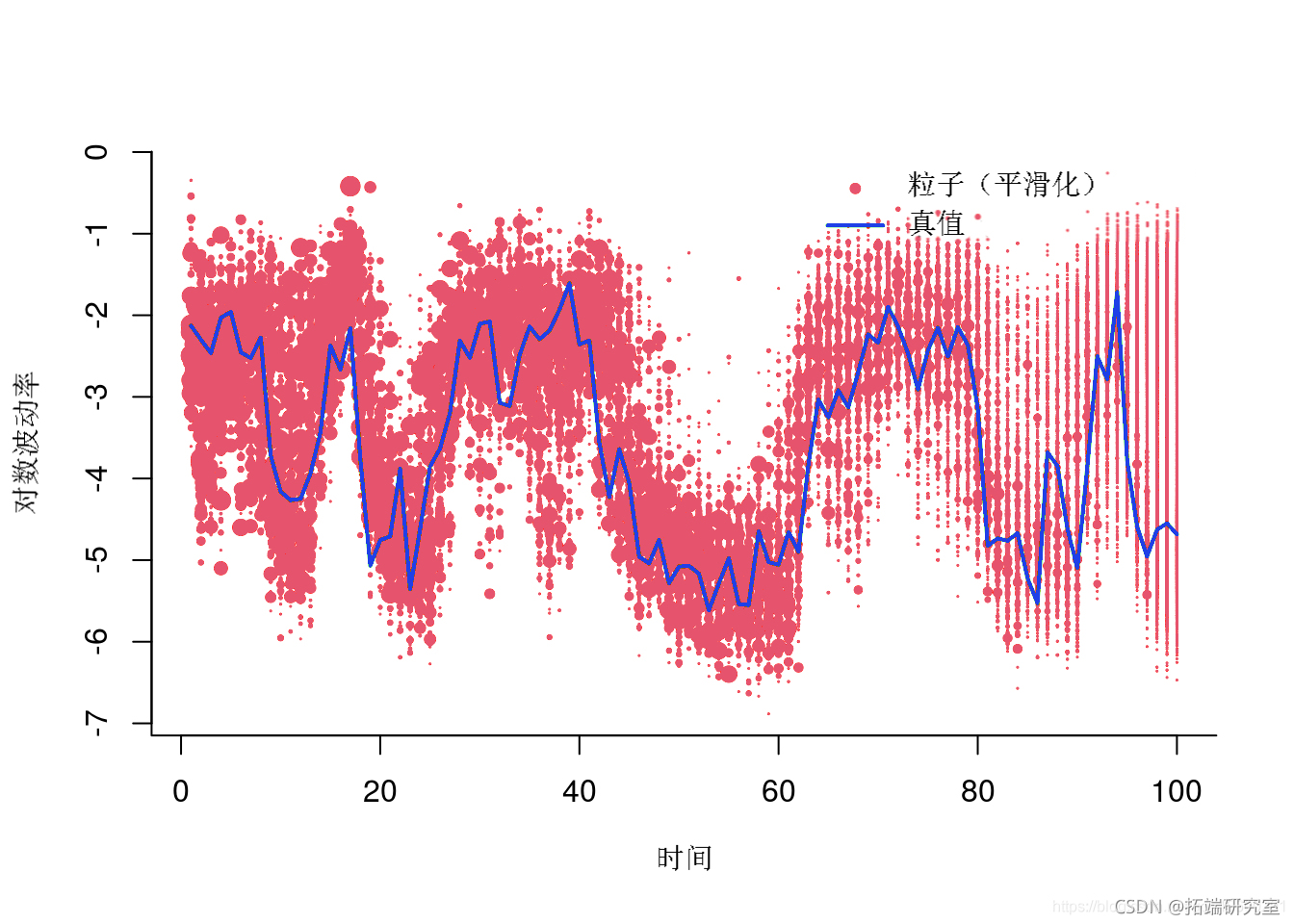
随时关注您喜欢的主题
粒子(平滑)
汇总统计
summary(out)
绘图滤波估计
men = mean qan = quant x = c(1:tmx, _a:1) y = c(fnt, ev(x__qat)) plot(x, y) pln(x, y, col) lines(1:tma,x_ean)
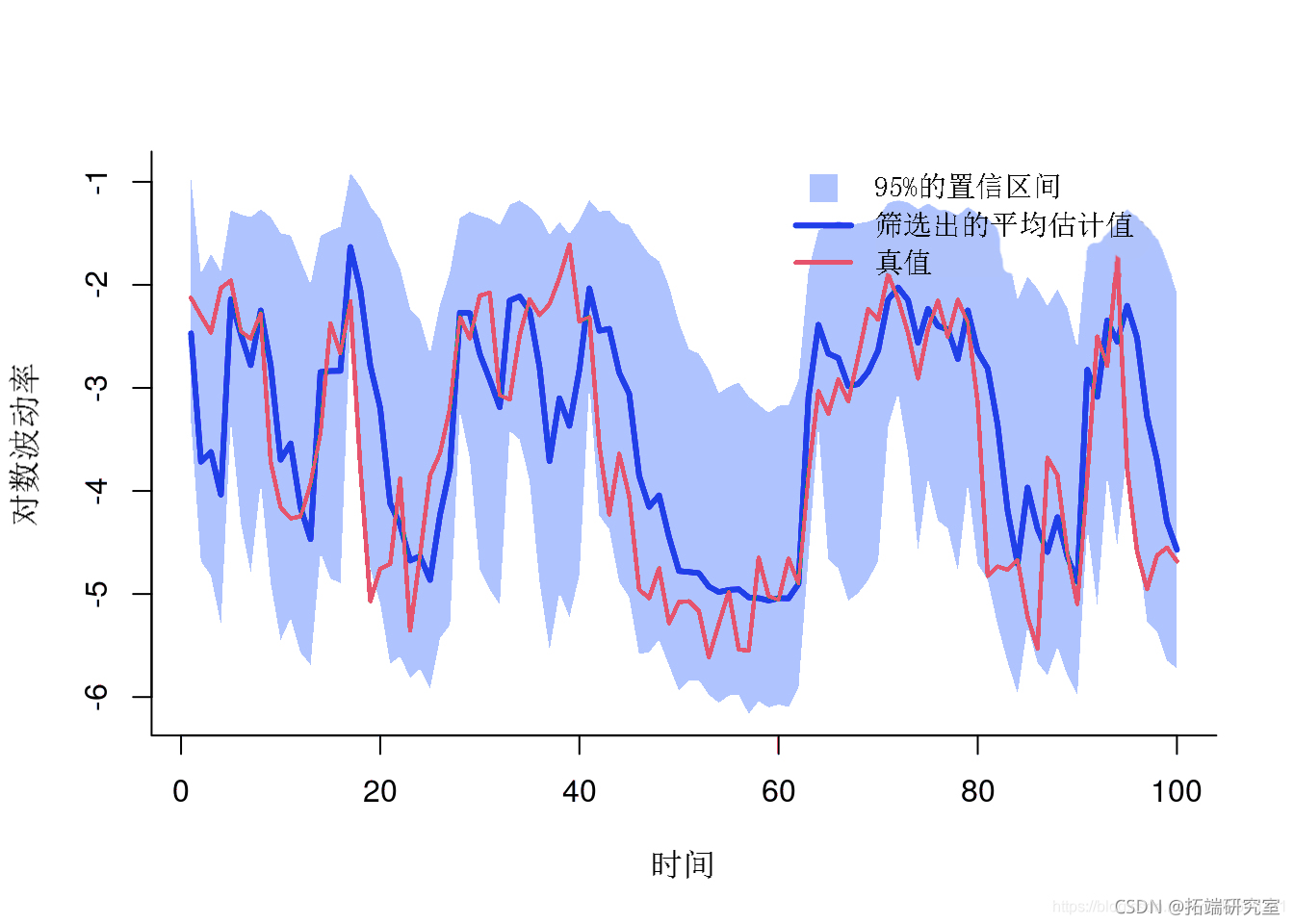
滤波估计
绘图平滑估计
plt(x,y, type='') polgon(x, y) lins(1:tmx, mean)
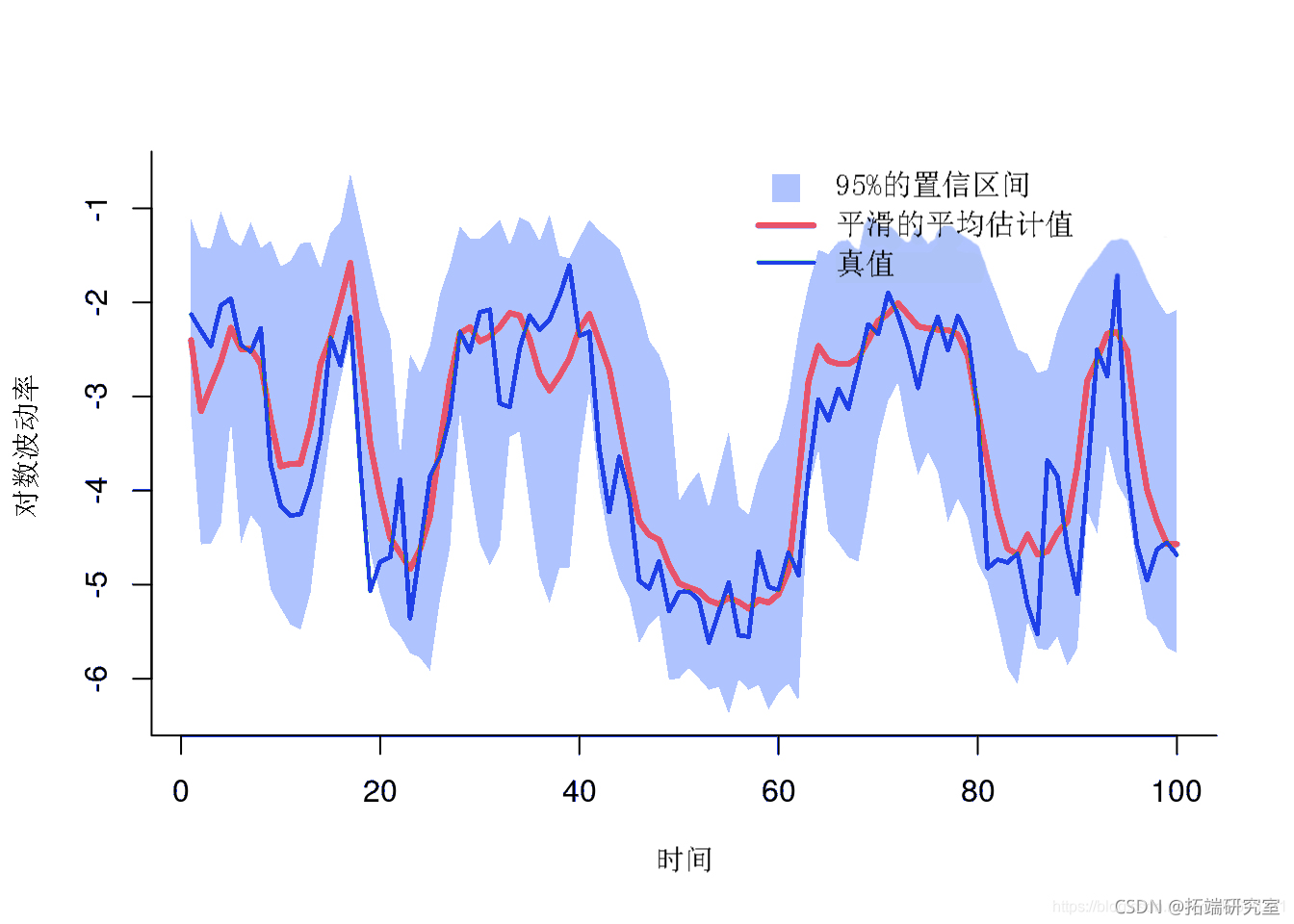
平滑估计
边缘滤波和平滑密度
denty(out)
indx = c(5, 10, 15)
for (k in 1:legh) {
inex
plt(x)
pints(xtrue\[k\])
}
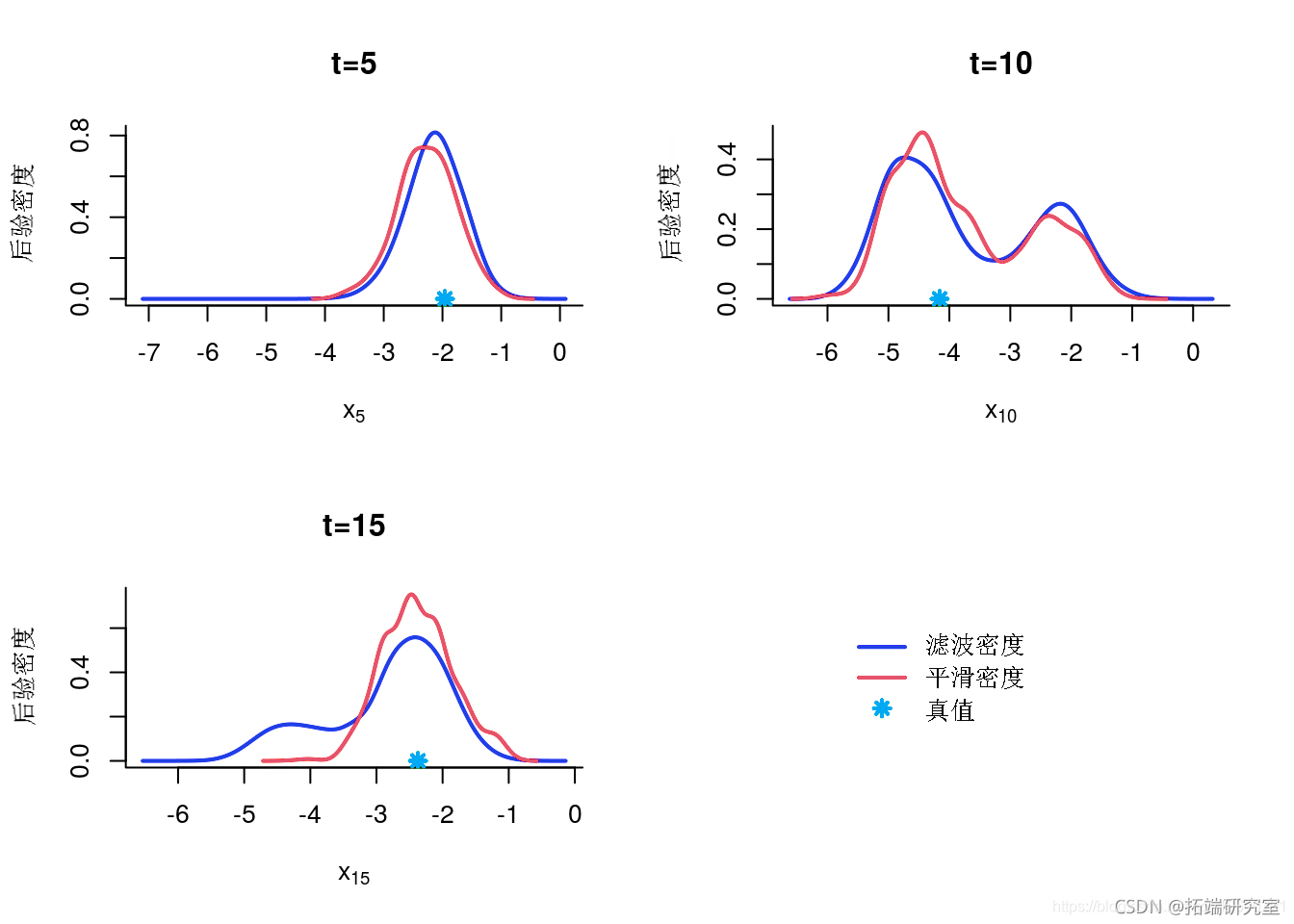
边缘后验
粒子独立 Metropolis-Hastings
运行
mh = mit(mol, vre)

mh(bm, brn, prt) # 预烧迭代

mh(bh, ni, n_at, hn=tn) # 返回样本

一些汇总统计
smay(otmh, pro=c(.025, .975))
后验均值和分位数
mean quant plot(x, y) polo(x, y, border=NA) lis(1:tax, mean)
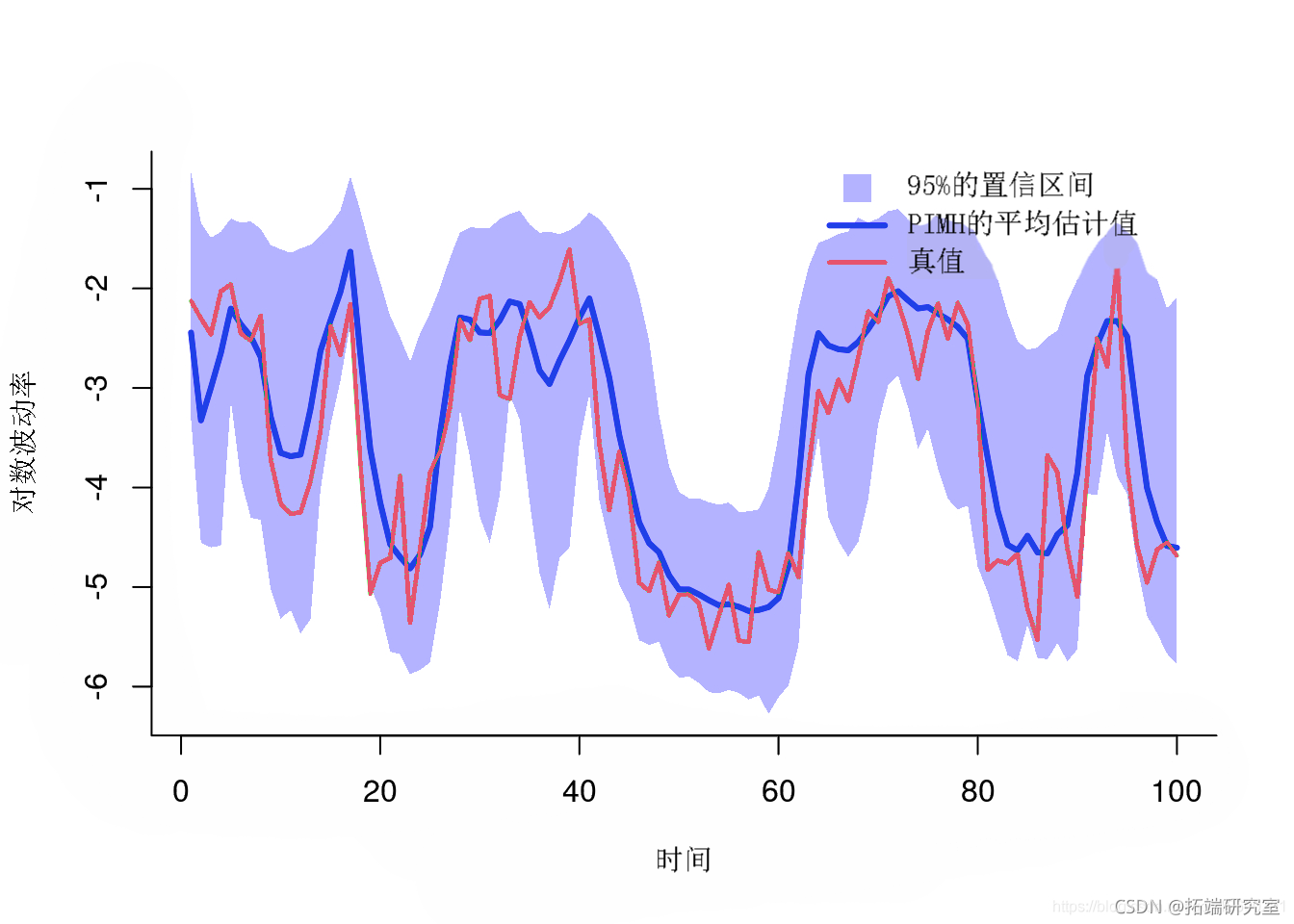
后验均值和分位数
MCMC 样本的踪迹图
for (k in 1:length {
tk = idx\[k\]
plot(out\[tk,\]
)
points(0, xtetk)
}
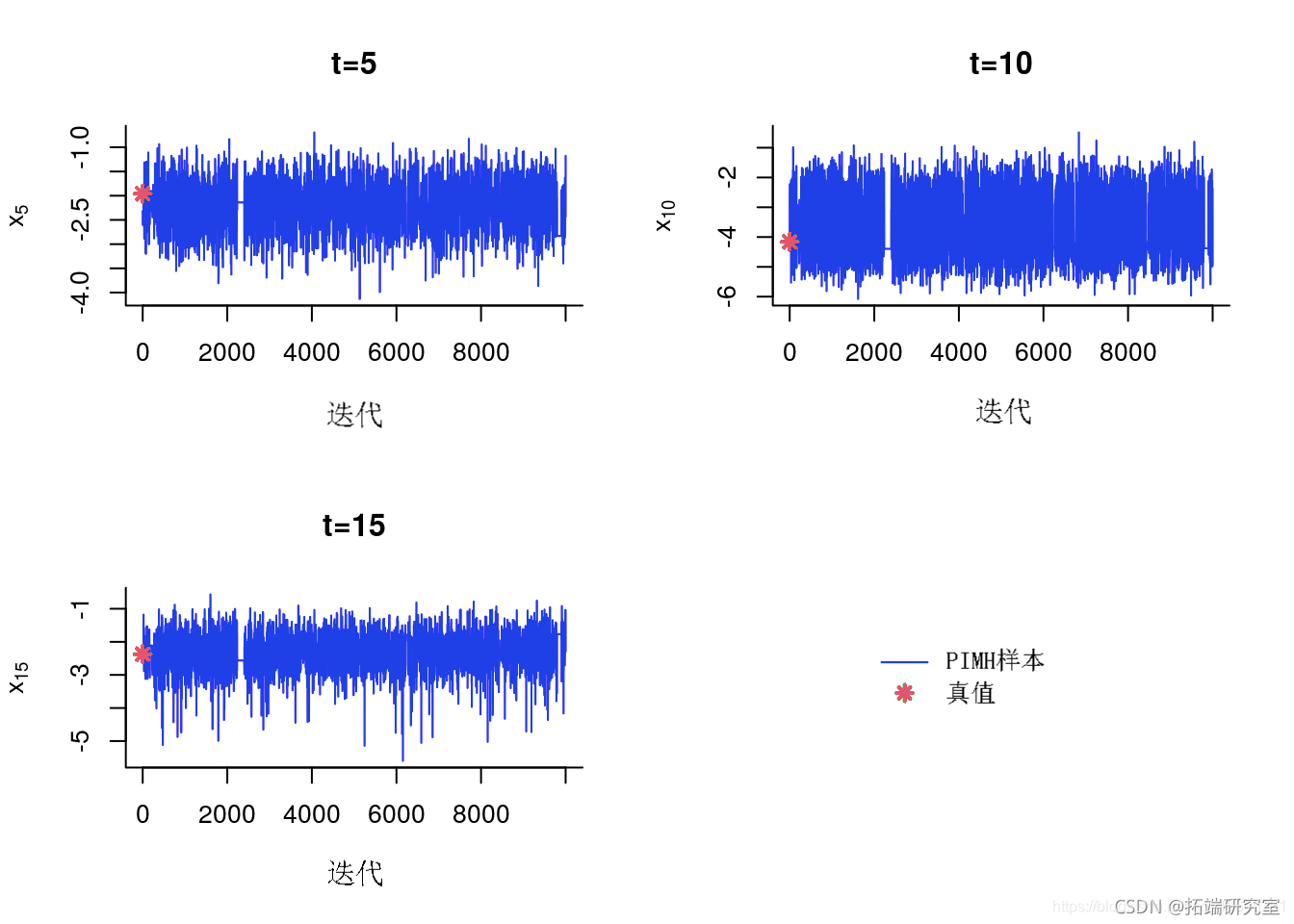
跟踪样本
后验直方图
for (k in 1:lngh) {
k = inex\[k\]
hit(mh$x\[t,\])
poits(true\[t\])
}
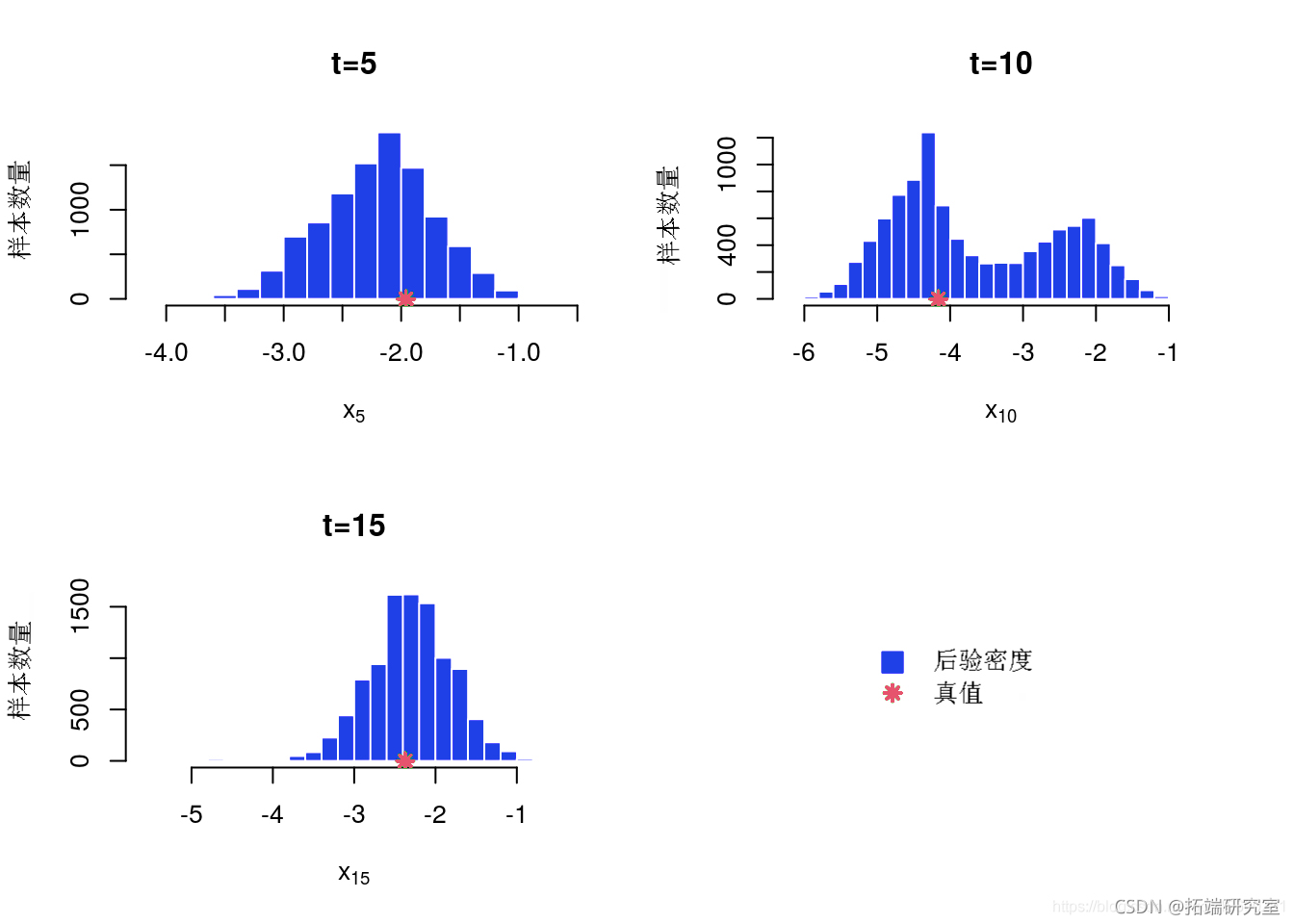
后边缘直方图
后验的核密度估计
for (k in 1:lnth(ie)) {
idx\[k\]
desty(out\[t,\])
plt(eim)
poit(xtu\[t\])
}
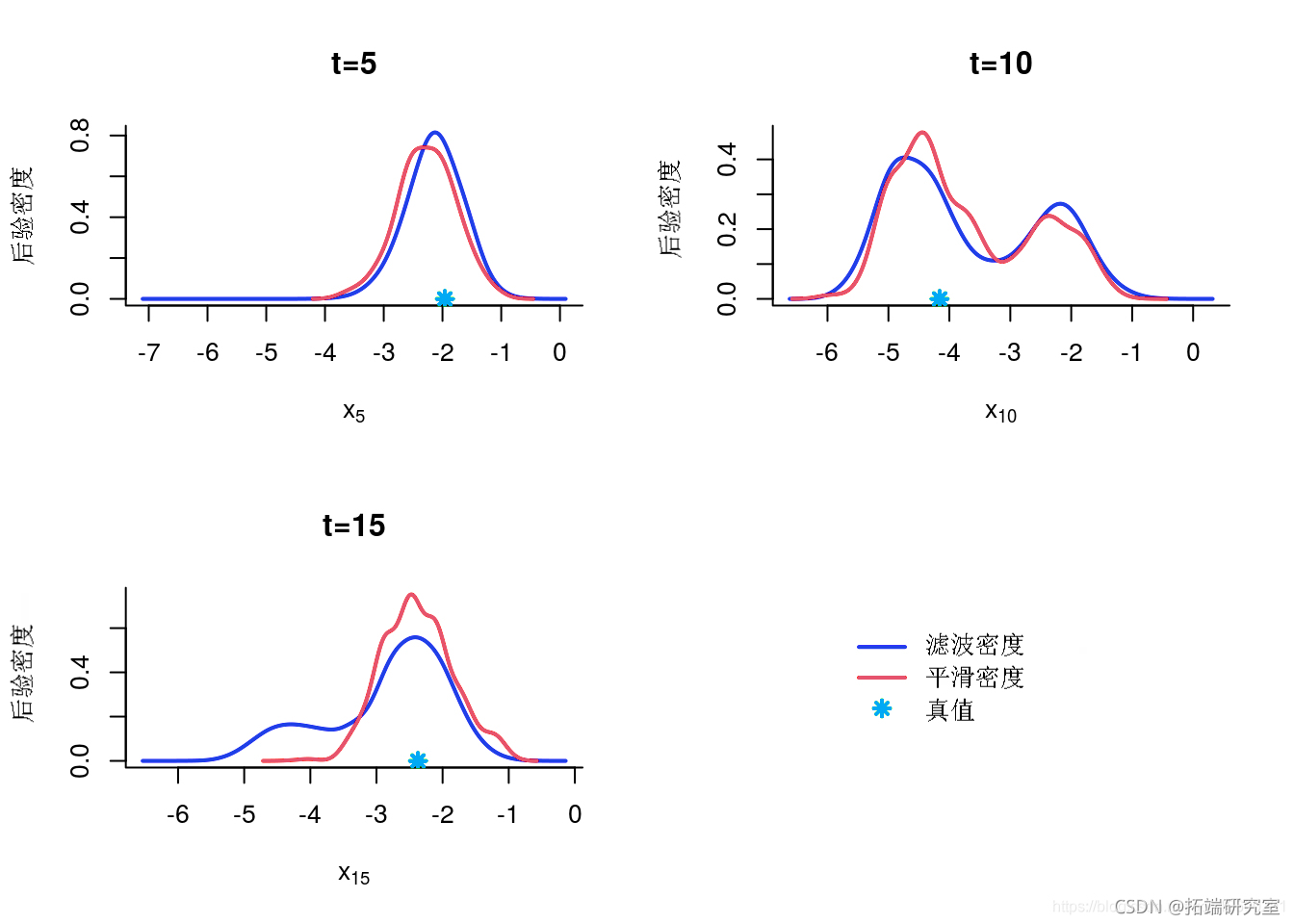
KDE 后验边缘估计
敏感性分析
我们想研究对参数 α 值的敏感性
算法参数
nr = 50 # 粒子的数量
gd <- seq(-5,2,.2) # 一个成分的数值网格
A = rep(grd, tes=leg) # 第一个成分的值
B = rep(grd, eah=lnh) # 第二个成分的值
vaue = ist('lph' = rid(A, B))
运行灵敏度分析
sny(oel,aaval, ar)

绘制对数边缘似然和惩罚对数边缘似然
# 通过阈值处理避免标准化问题 thr = -40 z = atx(mx(thr, utike), row=enth(rd))
plot(z, row=grd, col=grd, at=sq(thr))
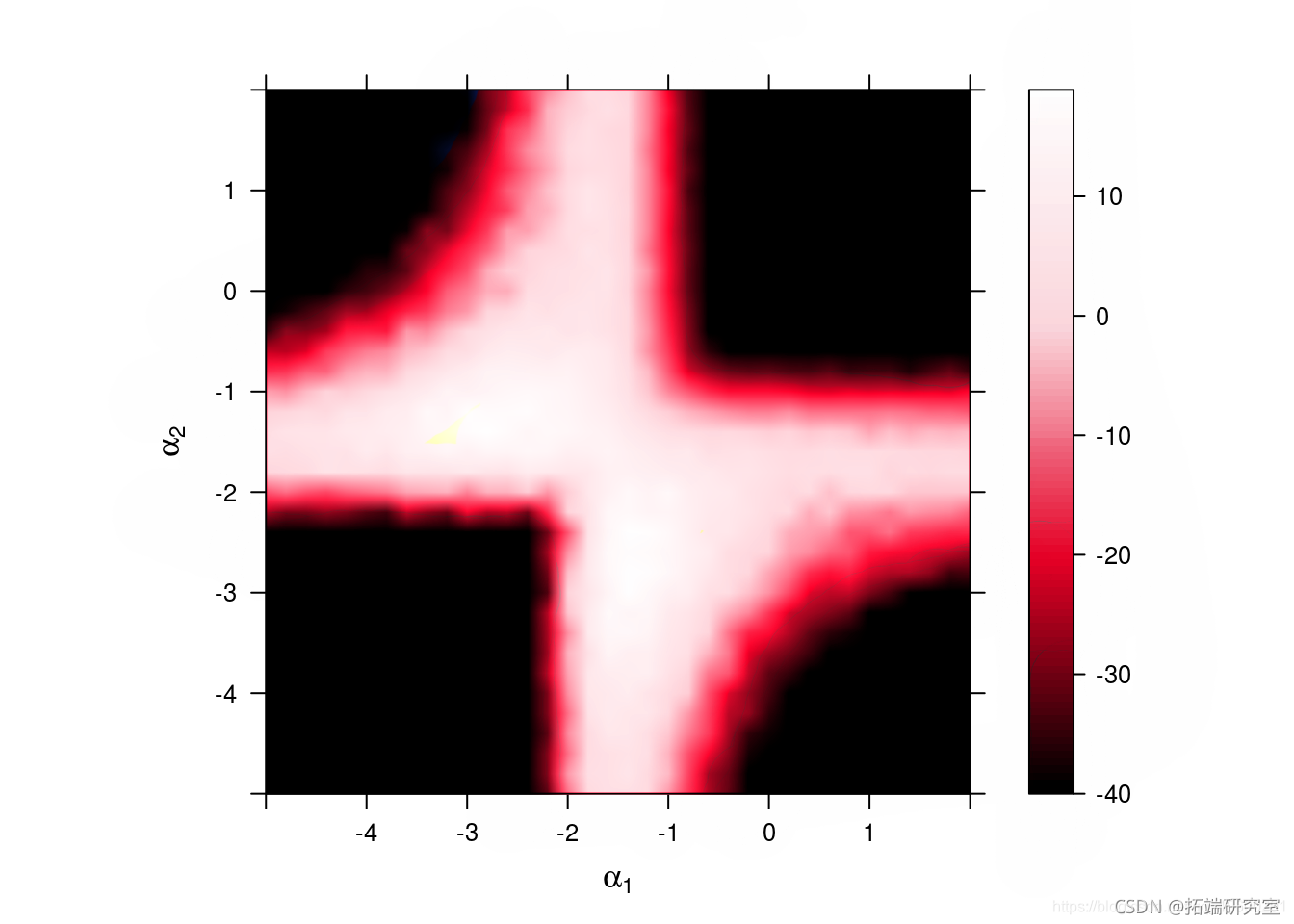
敏感性:对数似然
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 Python、SPSS单指数、FF三因子模型、决策树分析沪深300指数、申万风格指数、10年期国债收益率、300ETF期权波动率指数数据优化金融期货市场预测|附代码数据
Python、SPSS单指数、FF三因子模型、决策树分析沪深300指数、申万风格指数、10年期国债收益率、300ETF期权波动率指数数据优化金融期货市场预测|附代码数据 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略
Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略



