本文比较了几个时间序列模型，以预测SP 500指数的每日实际波动率。

由Kaizong Ye，Sherry Deng撰写

基准是SPX日收益系列的ARMA-EGARCH模型。将其与GARCH模型进行比较。最后，提出了集合预测算法。

可下载资源

假设条件

实际波动率是看不见的，因此我们只能对其进行估算。这也是波动率建模的难点。如果真实值未知，则很难判断预测质量。尽管如此，研究人员为实际波动率开发了估算模型。Andersen，Bollerslev Diebold（2008）和 Barndorff-Nielsen and Shephard（2007）以及 Shephard and Sheppard（2009）提出了一类基于高频的波动率（HEAVY）模型，作者认为HEAVY模型给出了 很好的 估计。

任何时间序列都由一个均值方程和一个方差方程所组成，普通的ARMA我们忽略了方差方程，因为残差是一个白噪声，没有任何信息可以挖掘了。所以一般只写一个ARMA。而 GARCH模型，我们平时都假设均值方程是一个常数，而残差有ARCH效应，所以就focus在残差上，均值略去不写。

所谓的ARMA-GARCH就是分别对均值和方差建模。即均值满足ARMA过程，残差满足GARCH过程的一个随机过程。

总结：
ARMA model: x~ARMA(p,q)+e, where e is a white noise
GARCH model: x~c+e, where c is a constant, e^2 follows a GARCH(p,q) process
ARMA-GARCH model: x~ARMA(p,q)+e, where e^2 follows a GARCH(m,n) process

假设：HEAVY实现的波动率估算器无偏且有效。

在下文中，将HEAVY估计量作为 观察到的已实现（实际）波动率 来确定预测性能。

数据来源

SPX每日数据（平仓收益）
SPX盘中高频数据（HEAVY模型估计）
VIX
VIX衍生品（VIX期货）

在本文中，我主要关注前两个。

数据采集

实际波动率估计和每日收益

我实现了Shephard和Sheppard的模型，并估计了SPX的实际量。

head(SPXdata)

               SPX2.rv       SPX2.r     SPX2.rs SPX2.nobs SPX2.open
2000-01-03 0.000157240 -0.010103618 0.000099500      1554  34191.16
2000-01-04 0.000298147 -0.039292183 0.000254283      1564  34195.04
2000-01-05 0.000307226  0.001749195 0.000138133      1552  34196.70
2000-01-06 0.000136238  0.001062120 0.000062000      1561  34191.43
2000-01-07 0.000092700  0.026022074 0.000024100      1540  34186.14
2000-01-10 0.000117787  0.010537636 0.000033700      1573  34191.50
           SPX2.highlow SPX2.highopen SPX2.openprice SPX2.closeprice
2000-01-03   0.02718625   0.005937756        1469.25         1454.48
2000-01-04   0.04052226   0.000000000        1455.22         1399.15
2000-01-05  -0.02550524   0.009848303        1399.42         1401.87
2000-01-06  -0.01418039   0.006958070        1402.11         1403.60
2000-01-07  -0.02806616   0.026126203        1403.45         1440.45
2000-01-10  -0.01575486   0.015754861        1441.47         1456.74
                 DATE   SPX2.rvol
2000-01-03 2000-01-03 0.012539537
2000-01-04 2000-01-04 0.017266934
2000-01-05 2000-01-05 0.017527864
2000-01-06 2000-01-06 0.011672103
2000-01-07 2000-01-07 0.009628084
2000-01-10 2000-01-10 0.010852972

视频

时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

SPXdata$SPX2.rv 是估计的实际方差。 SPXdata$SPX2.r 是每日收益（平仓/平仓）。 SPXdata$SPX2.rvol 是估计的实际波动率

基准模型：SPX每日收益率建模

ARMA-EGARCH

考虑到在条件方差中具有异方差性的每日收益，GARCH模型可以作为拟合和预测的基准。

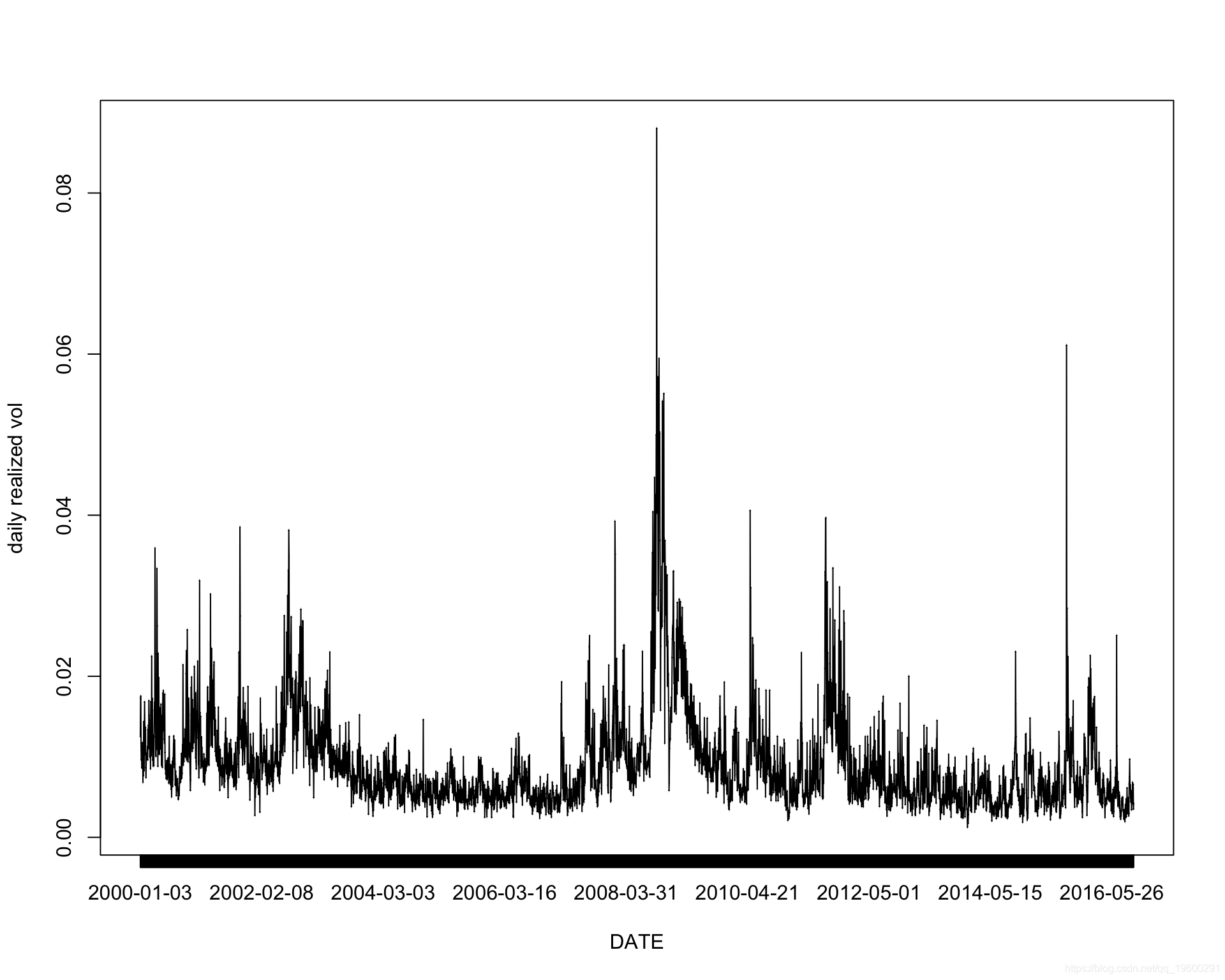
首先，收益序列是平稳的。


    Augmented Dickey-Fuller Test

data:  SPXdata$SPX2.r
Dickey-Fuller = -15.869, Lag order = 16, p-value = 0.01
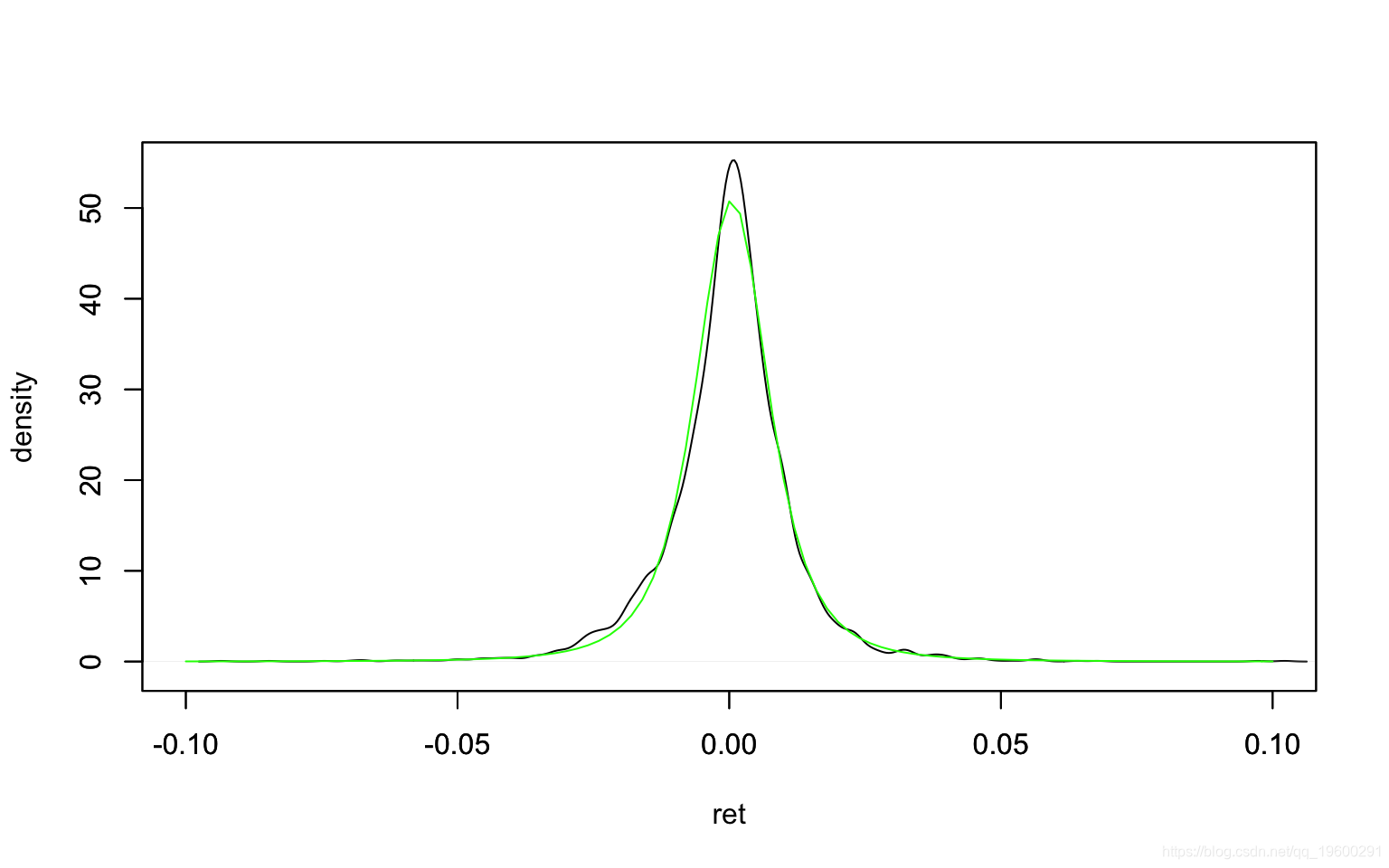
alternative hypothesis: stationary

分布显示出尖峰和厚尾。可以通过t分布回归分布密度图来近似。黑线是内核平滑的密度，绿线是t分布密度。

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.GARCH（1,1），MA以及历史模拟法的VaR比较

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.matlab预测ARMA-GARCH 条件均值和方差模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

acf(SPXdata$SPX2.r)  ##自相关系数图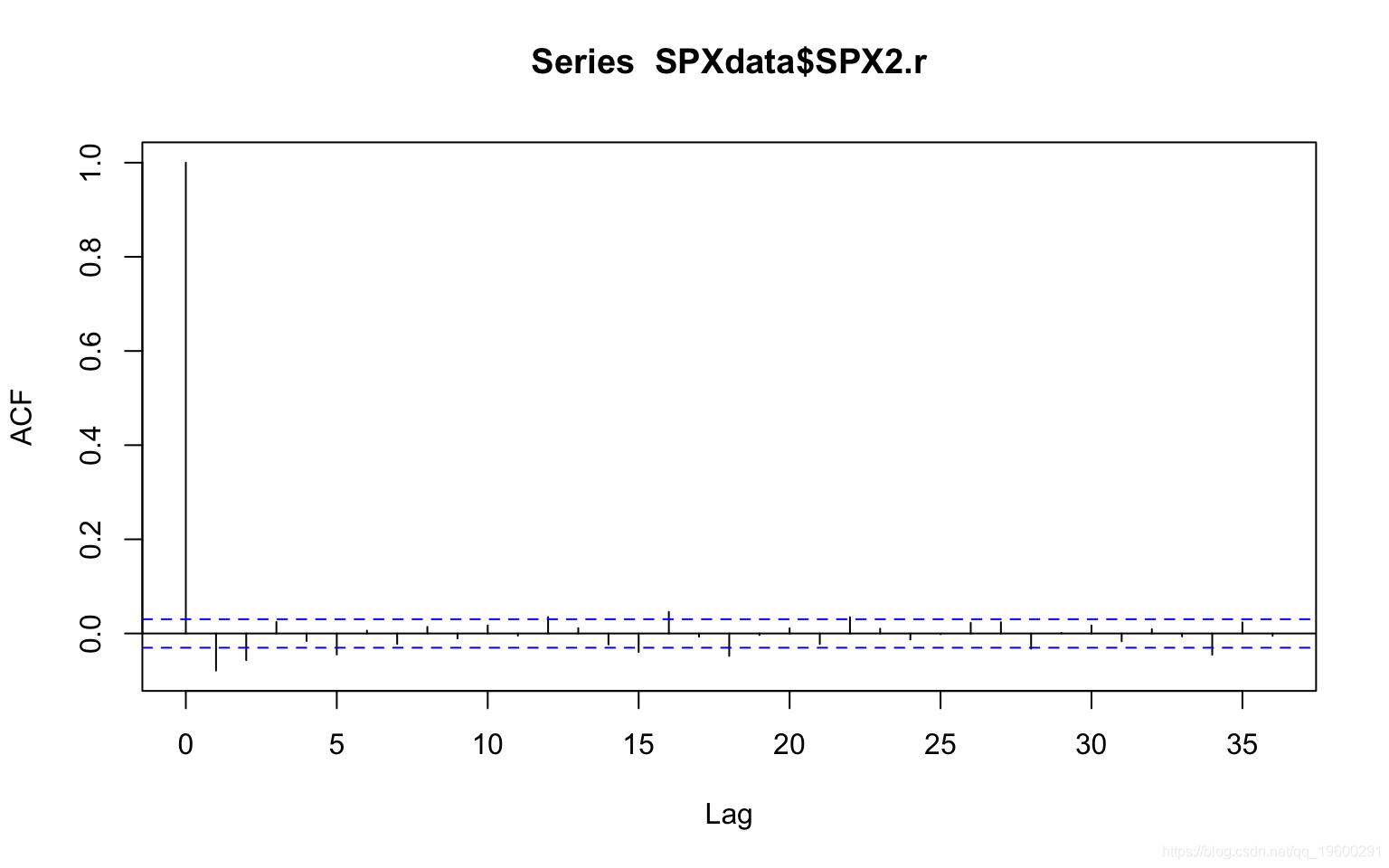


    Box-Ljung test

data:  SPXdata$SPX2.r
X-squared = 26.096, df = 1, p-value = 3.249e-07

R语言ARMA-GARCH-COPULA模型和金融时间序列案例

阅读文章 ➜

自相关图显示了每周相关性。Ljung-Box测试确认了序列存在相关性。

Series: SPXdata$SPX2.r 
ARIMA(2,0,0) with zero mean     

Coefficients:
          ar1      ar2
      -0.0839  -0.0633
s.e.   0.0154   0.0154

sigma^2 estimated as 0.0001412:  log likelihood=12624.97
AIC=-25243.94   AICc=-25243.93   BIC=-25224.92

auro.arima 表示ARIMA（2,0,0）可以对收益序列中的自相关进行建模，而eGARCH（1,1）在波动率建模中很受欢迎。因此，我选择具有t分布的ARMA（2,0）-eGARCH（1,1）作为基准模型。


*---------------------------------*
*       GARCH Model Spec          *
*---------------------------------*

Conditional Variance Dynamics   
------------------------------------
GARCH Model     : eGARCH(1,1)
Variance Targeting  : FALSE 

Conditional Mean Dynamics
------------------------------------
Mean Model      : ARFIMA(2,0,0)
Include Mean        : TRUE 
GARCH-in-Mean       : FALSE 

Conditional Distribution
------------------------------------
Distribution    :  std 
Includes Skew   :  FALSE 
Includes Shape  :  TRUE 
Includes Lambda :  FALSE

我用4189个观测值进行了回测（从2000-01-03到2016-10-06），使用前1000个观测值训练模型，然后每次向前滚动预测一个，然后每5个观测值重新估计模型一次。

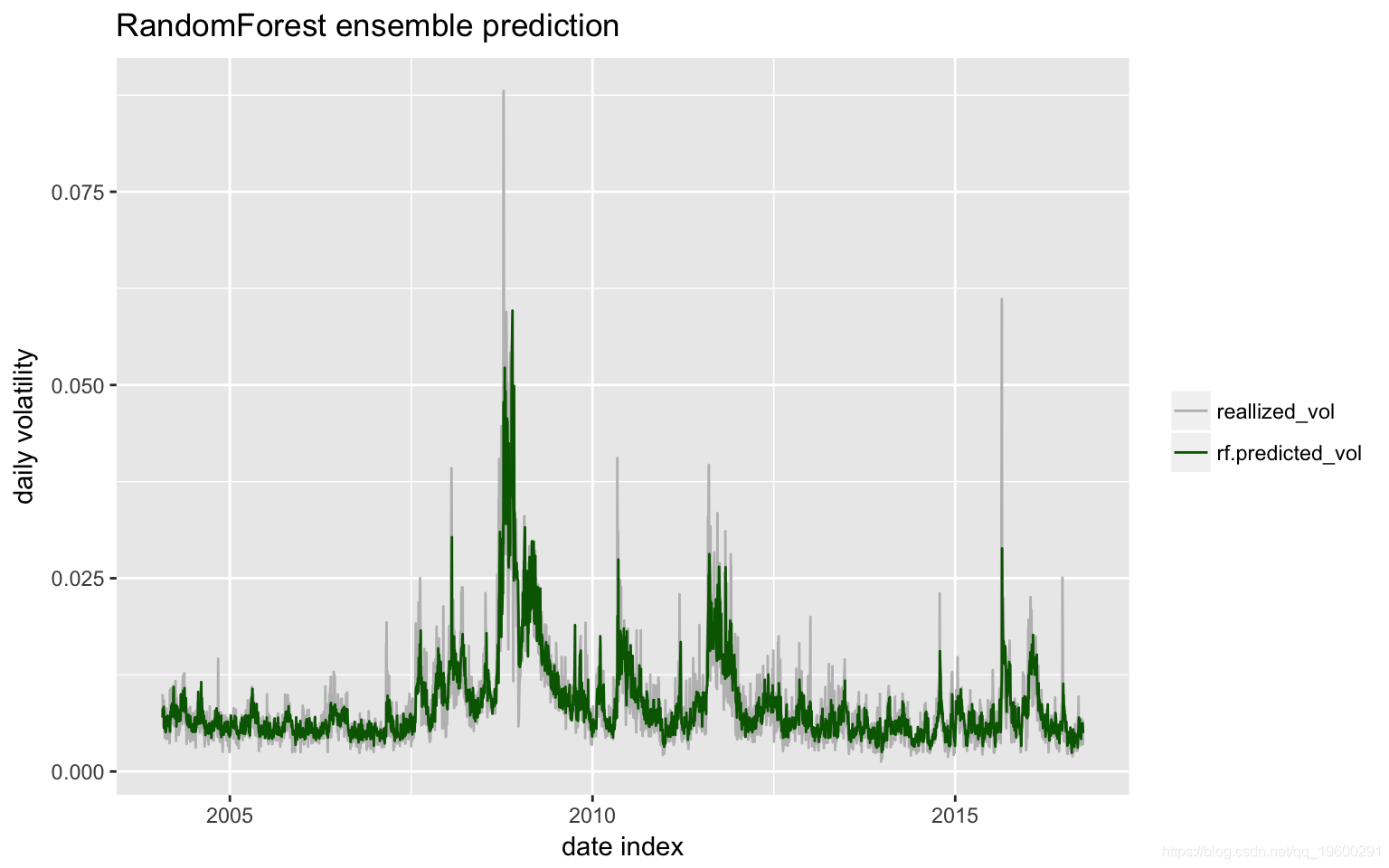
下图显示 了样本外 预测和相应的实际波动率。

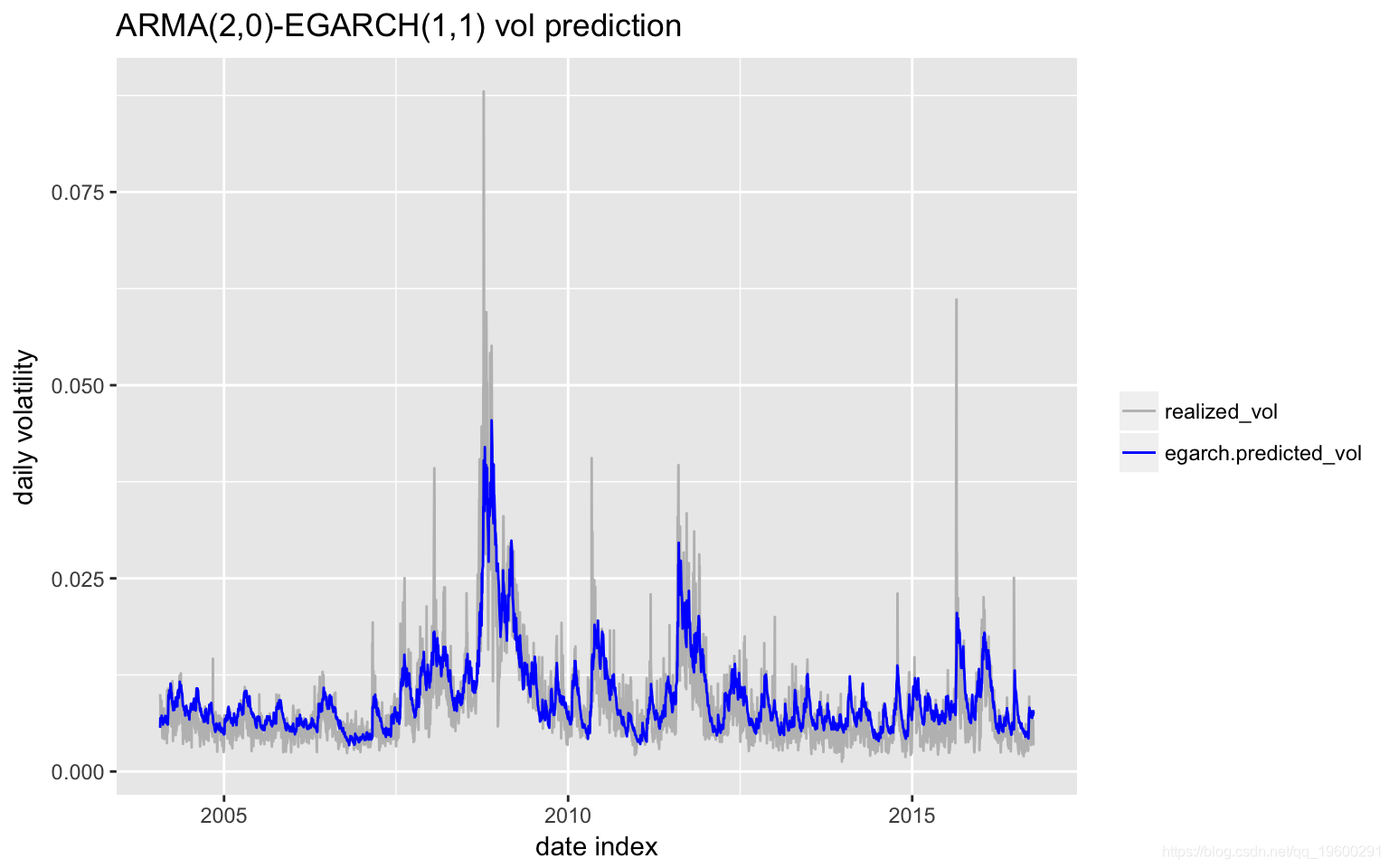
预测显示与实现波动率高度相关，超过72％。

cor(egarch_model$roll.pred$realized_vol, egarch_model$roll.pred$egarch.predicted_vol, 
    method = "spearman")

[1] 0.7228007

误差摘要和绘图

      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-0.0223800 -0.0027880 -0.0013160 -0.0009501  0.0003131  0.0477600

随时关注您喜欢的主题

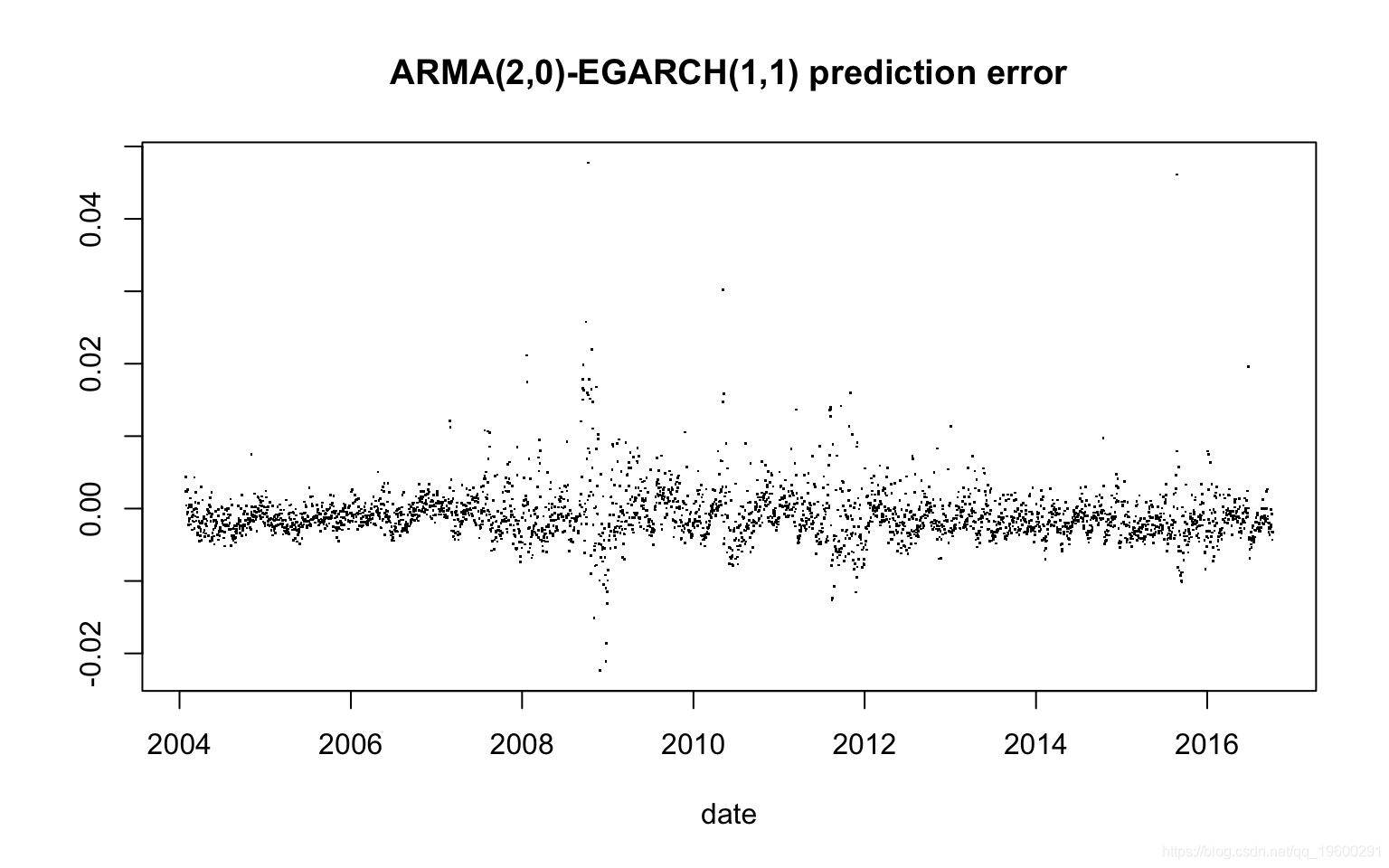
平均误差平方（MSE）：

[1] 1.351901e-05

改进：实际GARCH模型和LRD建模

realGARCH 该模型由 Hansen，Huang和Shek（2012）（HHS2012）提出，该模型使用非对称动力学表示将实际（已实现）波动率测度与潜在真实波动率联系起来。与标准GARCH模型不同，它是收益和实际波动率度量的联合建模（本文中的HEAVY估计器）。

实际GARCH

模型：


*---------------------------------*
*       GARCH Model Spec          *
*---------------------------------*

Conditional Variance Dynamics   
------------------------------------
GARCH Model     : realGARCH(2,1)
Variance Targeting  : FALSE 

Conditional Mean Dynamics
------------------------------------
Mean Model      : ARFIMA(2,0,0)
Include Mean        : TRUE 
GARCH-in-Mean       : FALSE 

Conditional Distribution
------------------------------------
Distribution    :  norm 
Includes Skew   :  FALSE 
Includes Shape  :  FALSE 
Includes Lambda :  FALSE

滚动预测过程与上述ARMA-EGARCH模型相同。下图显示了样本外预测和相应的实际波动率。

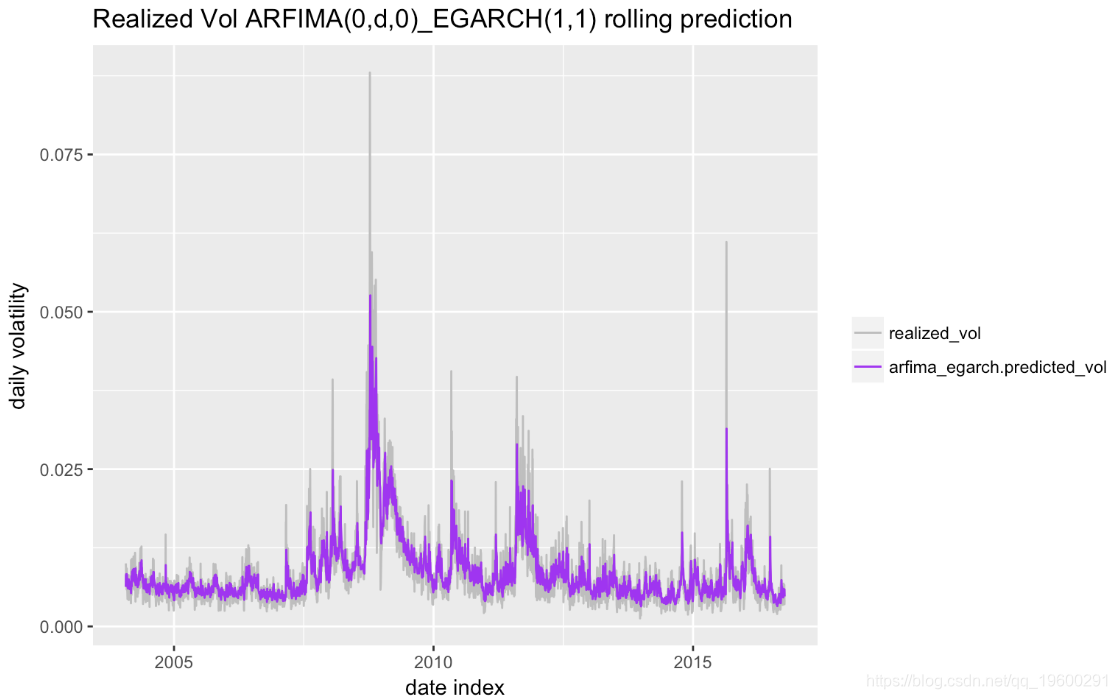
预测与实际的相关性超过77％

cor(arfima_egarch_model$roll.pred$realized_vol, arfima_egarch_model$roll.pred$arfima_egarch.predicted_vol, 
    method = "spearman")

[1] 0.7707991

误差摘要和图：

      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-1.851e-02 -1.665e-03 -4.912e-04 -1.828e-05  9.482e-04  5.462e-02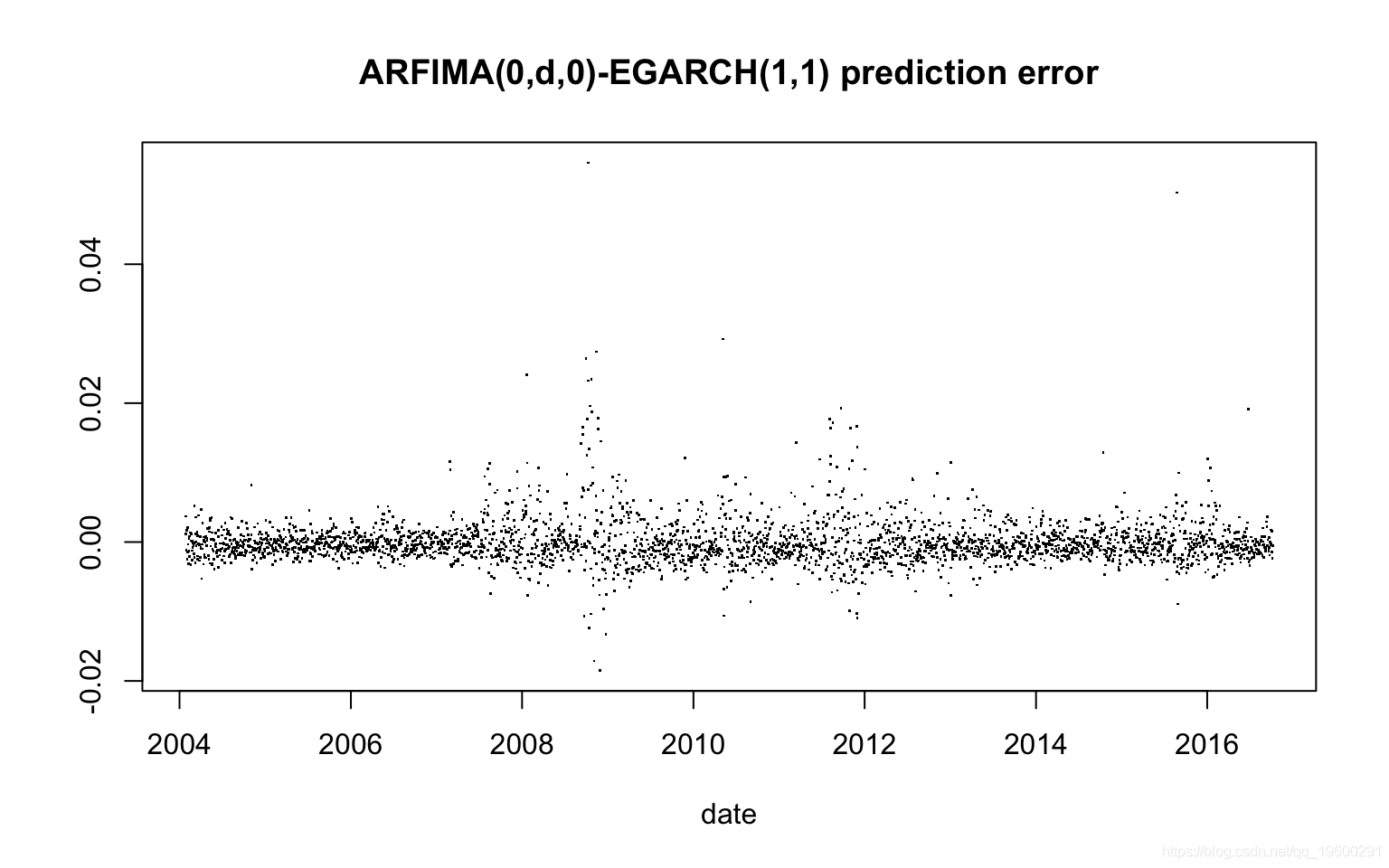

均方误差（MSE）：

[1] 1.18308e-05

备注：

用于每日收益序列的ARMA-eGARCH模型和用于实际波动率的ARFIMA-eGARCH模型利用不同的信息源。ARMA-eGARCH模型仅涉及每日收益，而ARFIMA-eGARCH模型基于HEAVY估算器，该估算器是根据日内数据计算得出的。RealGARCH模型将它们结合在一起。
以均方误差衡量，ARFIMA-eGARCH模型的性能略优于realGARCH模型。这可能是由于ARFIMA-eGARCH模型的LRD特性所致。

集成模型

随机森林

现在已经建立了三个预测

ARMA egarch_model
realGARCH rgarch model
ARFIMA-eGARCH arfima_egarch_model

尽管这三个预测显示出很高的相关性，但预计模型平均值会减少预测方差，从而提高准确性。使用了随机森林集成。

varImpPlot(rf$model)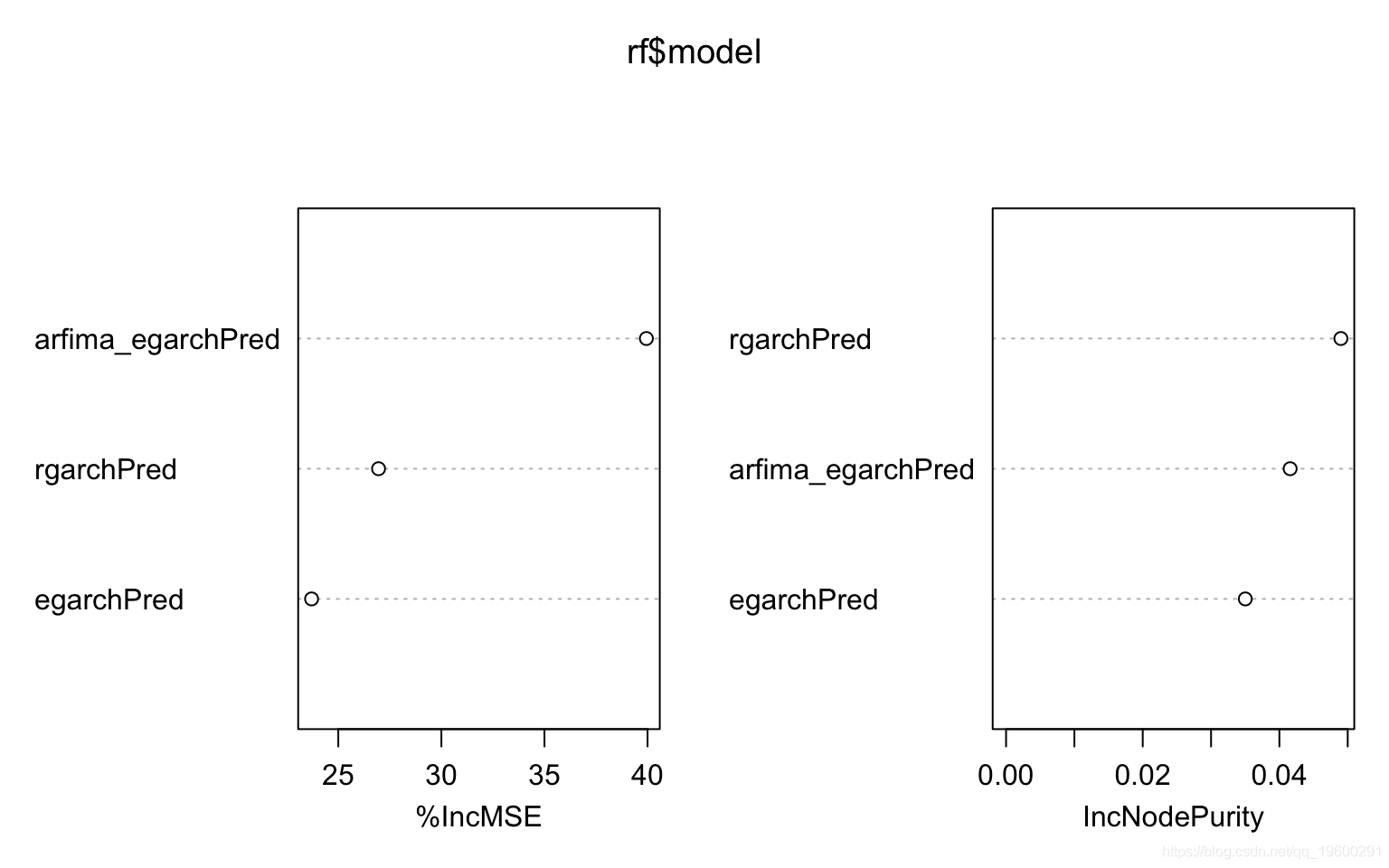

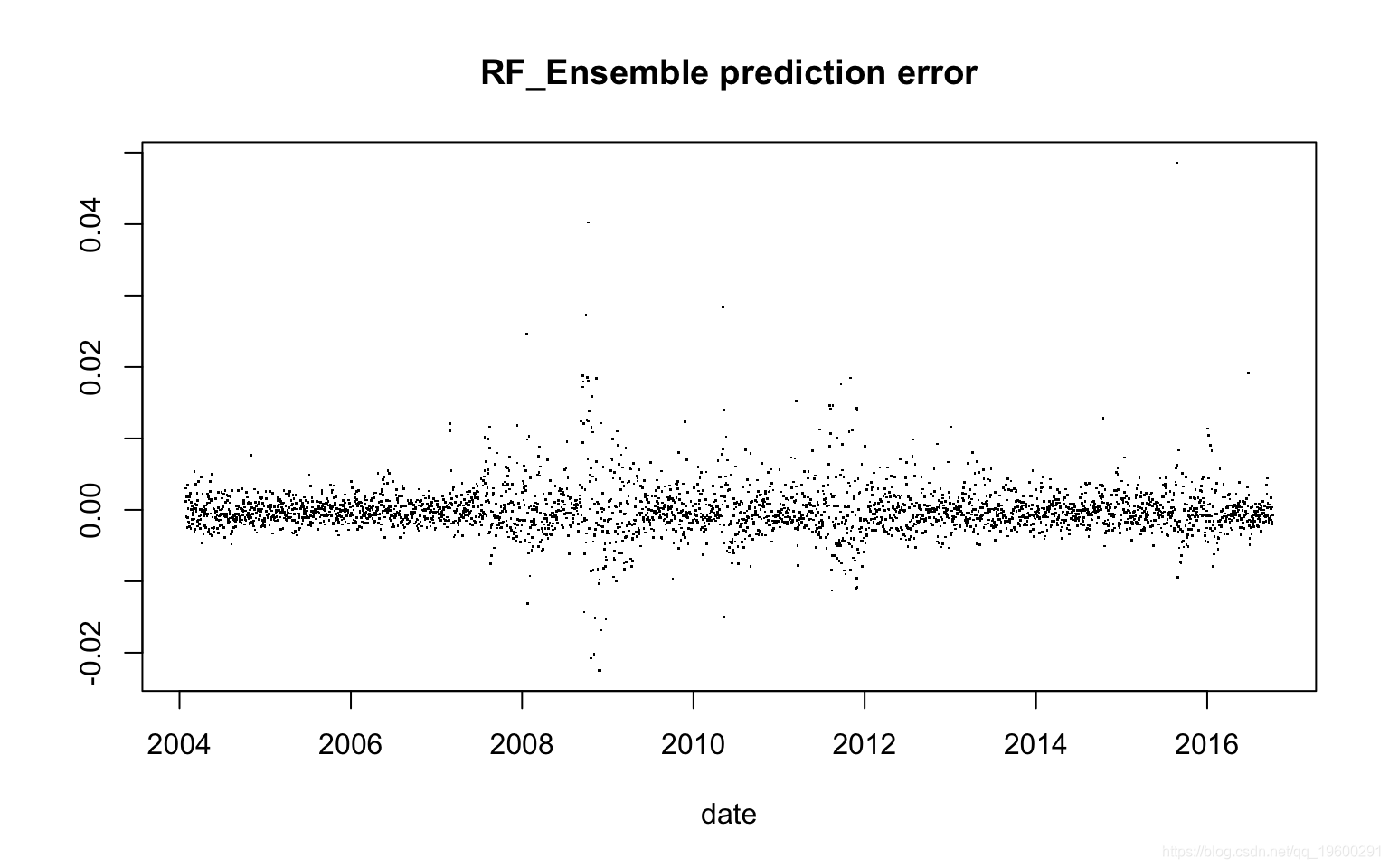
随机森林由500棵树组成，每棵树随机选择2个预测以适合实际值。下图是拟合和实际波动率。

预测与实际波动率的相关性：

[1] 0.840792

误差图：

均方误差：

[1] 1.197388e-05

MSE与实际波动率方差的比率

[1] 0.2983654

备注

涉及已实际量度信息的realGARCH模型和ARFIMA-eGARCH模型优于标准的收益序列ARMA-eGARCH模型。与基准相比，随机森林集成的MSE减少了17％以上。

从信息源的角度来看，realGARCH模型和ARFIMA-eGARCH模型捕获了日内高频数据中的增量信息（通过模型，HEAVY实际波动率估算）

进一步研究：隐含波动率

以上方法不包含隐含波动率数据。隐含波动率是根据SPX欧洲期权计算得出的。自然的看法是将隐含波动率作为预测已实现波动率的预测因子。但是，大量研究表明，无模型的隐含波动率VIX是有偏估计量，不如基于过去实际波动率的预测有效。 Torben G. Andersen，Per Frederiksen和Arne D. Staal（2007）同意这种观点。他们的工作表明，将隐含波动率引入时间序列分析框架不会带来任何明显的好处。但是，作者指出了隐含波动率中增量信息的可能性，并提出了组合模型。

因此，进一步的发展可能是将时间序列预测和隐含波动率（如果存在）的预测信息相结合的集成模型。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测