
主成分分析法是数据挖掘中常用的一种降维算法。
PCA(主成分分析)是Pearson在1901年提出的,再后来由hotelling在1933年加以发展提出的一种多变量的统计方法,其最主要的用途在于“降维”,通过析取主成分显出的最大的个别差异,也可以用来削减回归分析和聚类分析中变量的数目,与因子分析类似。
所谓降维,就是把具有相关性的变量数目减少,用较少的变量来取代原先变量。如果原始变量互相正交,即没有相关性,则主成分分析没有效果。
可下载资源
对应分析(CA)是适用于分析由两个定性变量(或分类数据)形成的大型应变表的主成分分析的扩展。本文通过析取主成分来分析夫妻职业的个别差异。
主成分分析是因子分析的特例,因为主成分可以看成是潜在因子,则主成分就是因子分析的一个解。为了说明的简单,将主成分分析和因子分析合并,统一用“因子分析”来指代。
因子分析的目标是寻找(探索)潜在因子,因子到底是什么,其实并不知道,要通过因子分析去探索得到。最终结果是得到因子或者得不到因子,得不到因子表示因子分析失败。得到因子后可以计算因子得分,每个因子当成一个维度,则可以在空间中把每个个案显示出来。为了适合人观察,会选取前面两个或者三个因子,个案就可以在二维空间显示。因为空间的维度就是因子,所以基于因子分析得到的空间图的坐标有实际的意义。
对应分析的目标是把行列轮廓在高维空间的图低损失(不失真)的投影到低维空间,方便我们观看轮廓之间的关系。对应分析得到的空间图的坐标不一定有实际意义。在图上可以比较行轮廓(列轮廓)之间的相似性,行(列)轮廓之间距离越近表示越相近,以及行列变量之间占比关系。
多维尺度(Multidimensional Scaling-MDS)分析的目标是将对象间的差异(或相似性)通过图形展示出来,图中两点的距离表示对象差异,距离越远表示两个对象差异越大,距离越近表示两个对象差异越小。空间图的坐标不一定有实际意义。MDS中的“个体差异分析”、“评分分析或Unfolding”不做进一步的说明,因为无实质性意义,所以MDS指代所有的MDS模型。
夫妻职业数据
考虑以下数据,对应于一对夫妻中的职业。我们有以下的频数表
read.table(data.csv",header=TRUE)
传统上,对于这种数据,我们习惯于使用卡方检验,卡方距离,以及卡方贡献来查看数据的差异性
chisq.test(M)
马赛克图
Mosaic plot常常用来展示Categorical data(分类数据)(关于不同的数据类别,mosaic plot 强大的地方在于它能够很好的展示出2个或者多个分类型变量(categorical variable)的关系. 它也可以定义为用图像的方式展示分类型数据。
当变量是类别变量时,且数目多于三个的时候,可使用马赛克图。马赛克图中,嵌套矩阵面积正比于单元格频率,其中该频率即多维列联表中的频率。颜色和阴影可表示拟合模型的残差值。
我们可以将其结果用马赛克图来形象化。
plot(tM)丈夫在行中,妻子在列中。重要的联系是蓝色或红色,这两种颜色分别对应于 “正 “联系(比独立情况下的联合概率高)或 “负 “联系(比独立情况下的联合概率低)。
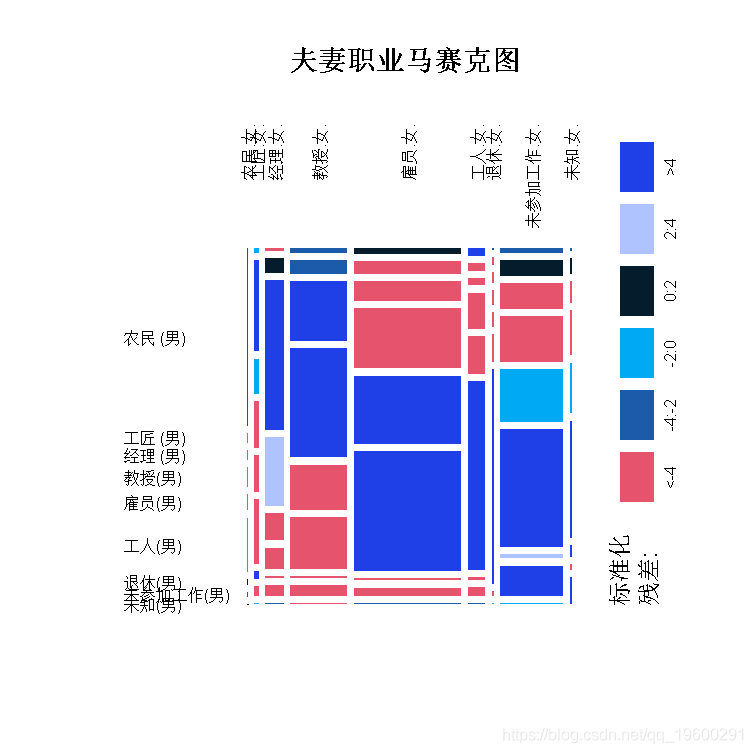
在另一个方向
plot(M)但结论与之前一样:对角线上有很强的蓝色数值。
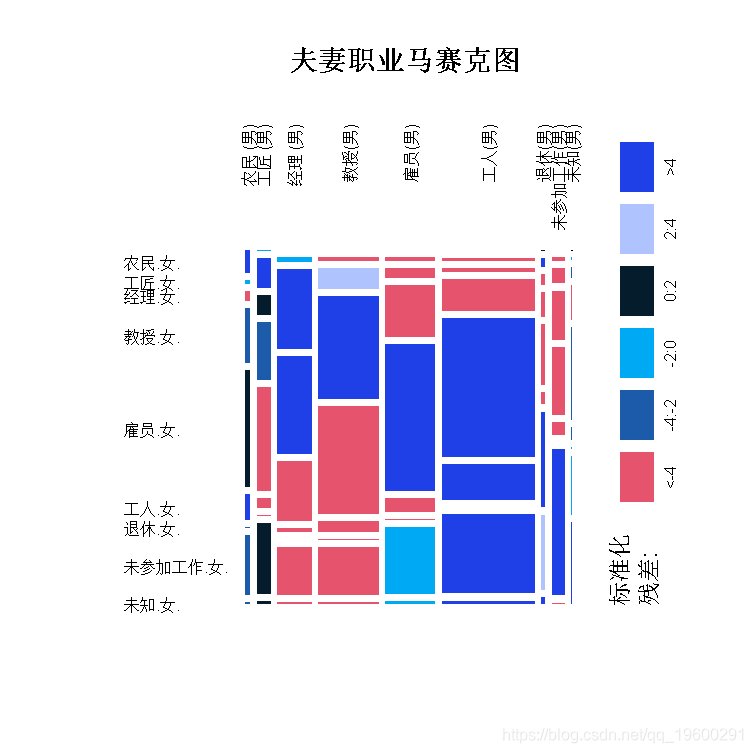
换句话说,这些夫妻在职业方面是相对相似和单一的。
主成分分析和对应分析
在对应分析中,我们查看概率表,在行或列中。例如,我们可以定义行,它是概率向量
随时关注您喜欢的主题
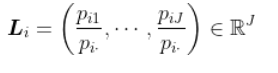
N/apply(N,1,sum)注意到 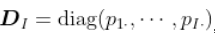 ,我们可以写出
,我们可以写出
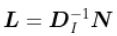
我们的线向量的重心在这里

同样,注意到 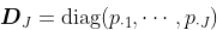 , 我们可以用矩阵的方式来写,
, 我们可以用矩阵的方式来写, 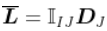 .
.
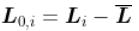
L0=(t(L)-Lbar)对于每一个点,我们都将(相对)频率作为权重进行关联,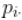 这相当于使用矩阵 。为了测量两点之间的距离
这相当于使用矩阵 。为了测量两点之间的距离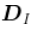 ,我们将通过概率的倒数对欧氏距离进行加权,
,我们将通过概率的倒数对欧氏距离进行加权,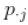 。两条线之间的距离是
。两条线之间的距离是
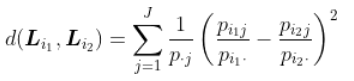
然后我们将用这些不同的权重做主成分分析。从矩阵的角度来看
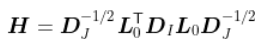
我们注意到特征向量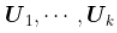 ,我们定义了主成分
,我们定义了主成分
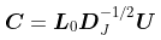
对线条的前两个成分的投影,在此给出了
PCA(L0,scal=FALSE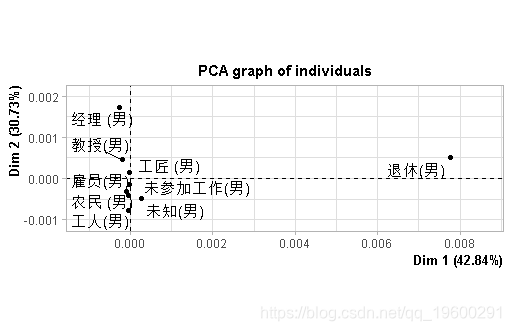
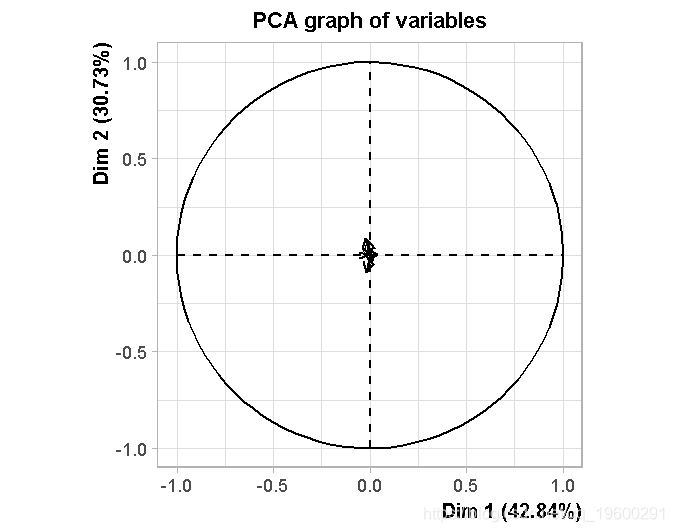
我们的想法是将对应于行的个体进行可视化。在第二步中,我们做相同的事情,在列中
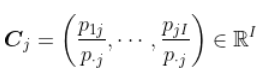
N/apply(N,2,sum))中心:
![]()
C0=C-Cbar然后我们可以做一个主成分分析,看个人的可视化。
主成分分析
PCA(matC0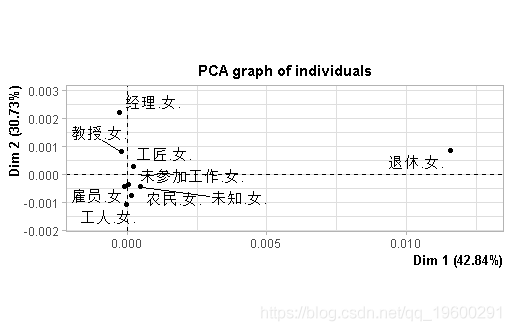
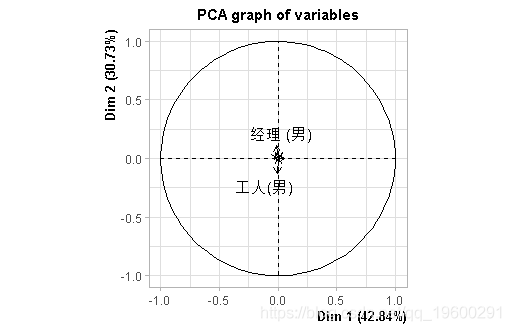
对应分析
对应分析的奇妙之处在于,我们 “可以 “在同一平面上表示个人的两个投影。
> plot(C\[,1:2\])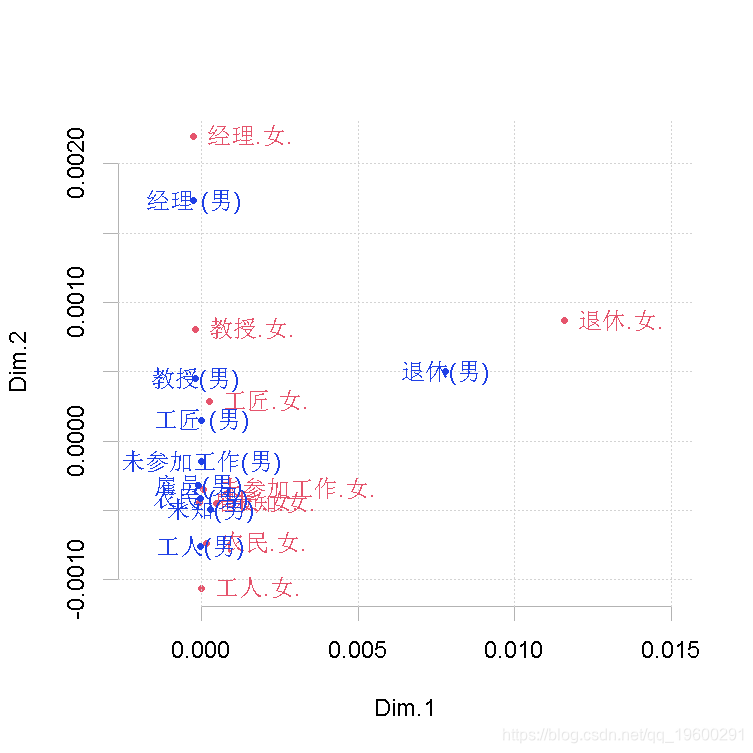
结果如下
> afc=CA(N)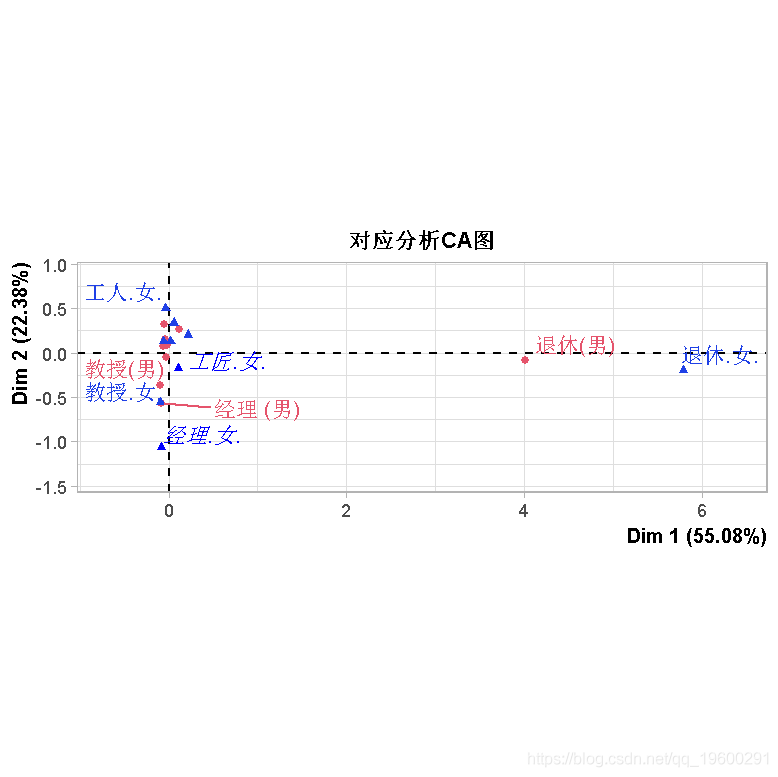
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载
2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载
