我们在研究人口数据集，可以观察到很多波动性。

由Kaizong Ye，Sherry Deng撰写

我们得到这样的结果：

可下载资源

Lee-Carter模型的主要思路是将死亡率的变化分解为时间因子t和年龄因子x。如果用表示x岁的人群在第t年的中心死亡率，那么满足以下函数关系式。

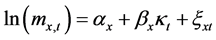(1)

其中，反应x岁年龄组别的对数中心死亡率的平均水平，为人口死亡率随时间变化的速度，为年龄因子对的敏感度，即x岁年龄组别的死亡率随着时间变化的大小，为随机误差项，假设其服从正态分布。为了得到唯一确定的参数估计值，加入约束条件以及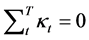。是为了保证参数的平均值的含义，即。

模型的求解

Lee-Carter模型参数的估计方法主要包括矩阵奇异值分解法(SVD)、最小二乘(OLS)和加权最小二乘法(WLS)；奇异值分解法和最小二乘法对不同年龄人群的死亡率赋予了相同的权重，但Koissi [2] 证明了，在现实情况下，不同年龄人群对应的人口数和死亡人口数都存在较大的差异，因此这两种方法在死亡率很低的条件下使用效果较差。为此，本文采用加权最小二乘法来估计Lee-Carter模型。

加权最小二乘法通过以下两个步骤求得，

第一步，将式(1)两边对年龄x 求和，得到。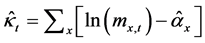

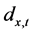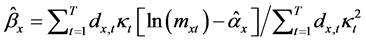第二步，Wilmoth [3] 证明的方差近似等于死亡人数的倒数，因此可以将作为残差平方和的权重。最小化经加权处理后的残差平方和，即得到 [4] 。

由于我们缺少一些数据，因此我们想使用一些广义非线性模型。因此，让我们看看如何获得死亡率曲面图的平滑估计。我们编写一些代码。


D=DEATH$Male
E=EXPO$Male
A=as.numeric(as.character(DEATH$Age))
Y=DEATH$Year
I=(A<100)
base=data.frame(D=D,E=E,Y=Y,A=A)
subbase=base[I,]
subbase=subbase[!is.na(subbase$A),]

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

第一个想法可以是使用Poisson模型，其中死亡率是年龄和年份的平稳函数，类似于

可以使用


persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

死亡率曲面图

还可以提取年份的平均值，这是 $a_x$ Lee-Carter模型中系数的解释

predAx=function(a) mean(predict(regbsp,newdata=data.frame(A=a,
Y=seq(min(subbase$Y),max(subbase$Y)),E=1)))
plot(seq(0,99),Vectorize(predAx)(seq(0,99)),col="red",lwd=3,type="l")

我们有以下平滑的死亡率

回顾下李·卡特模型是

最受欢迎的见解

1.用SPSS估计HLM层次线性模型模型

2.R语言线性判别分析（LDA），二次判别分析（QDA）和正则判别分析（RDA）

3.基于R语言的lmer混合线性回归模型

4.R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

5.在r语言中使用GAM（广义相加模型）进行电力负荷时间序列分析

6.使用SAS，Stata，HLM，R，SPSS和Mplus的分层线性模型HLM

7.R语言中的岭回归、套索回归、主成分回归：线性模型选择和正则化

8.R语言用线性回归模型预测空气质量臭氧数据

9.R语言分层线性模型案例

可以使用以下方法获得参数估计值

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

粗略的死亡率曲面图是

有以下 $a_x$ 系数。

plot(seq(1,99),coefficients(regnp)[2:100],col="red",lwd=3,type="l")

这里我们有很多系数，但是，在较小的数据集上，我们具有更多的可变性。我们可以平滑李·卡特模型：

R语言Lee-Carter模型对年死亡率建模预测期望寿命

阅读文章 ➜

代码片段


persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)", 
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

现在的死亡人数是

得出多年来随年龄变化的平均死亡率，

随时关注您喜欢的主题

BpA=bs(seq(0,99),knots=knotsA,Boundary.knots=range(subbase$A),degre=3)
Ax=BpA%*%coefficients(regsp)[2:8]
plot(seq(0,99),Ax,col="red",lwd=3,type="l")

然后，我们可以使用样条函数的平滑参数，并查看对死亡率曲面的影响

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言预测人口死亡率：用李·卡特（Lee-Carter）模型、非线性模型进行平滑估计

R语言Lee-Carter模型对年死亡率建模预测期望寿命

随时关注您喜欢的主题

相关文章

R语言预测人口死亡率：用李·卡特（Lee-Carter）模型、非线性模型进行平滑估计

R语言Lee-Carter模型对年死亡率建模预测期望寿命

随时关注您喜欢的主题

相关文章

关注有关新文章的微信公众号