变量重要性图是查看模型中哪些变量有趣的好工具。
由于我们通常在随机森林中使用它，因此它看起来非常适合非常大的数据集。
可下载资源
大型数据集的问题在于许多特征是“相关的”，在这种情况下，很难比较可变重要性图的值的解释。例如，考虑一个非常简单的线性模型。
在这里，我们使用一个随机森林的特征之间的关系模型，但实际上，我们考虑另一个特点-不用于产生数据X2，即相关X1。我们考虑这三个特征的随机森林 。
为了获得更可靠的结果，我生成了100个大小为1,000的数据集。
library(mnormt)
RF=randomForest(Y~.,data=db)
plot(C,VI[1,],type="l",col="red")
lines(C,VI[2,],col="blue")
lines(C,VI[3,],col="purple")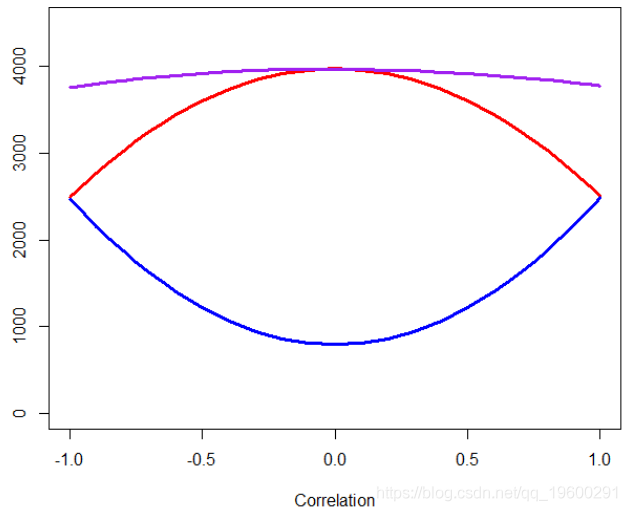
顶部的紫色线是的可变重要性值 X3，该值相当稳定（作为一阶近似值，几乎恒定）。红线是的变量重要性函数， X1 蓝线是的变量重要性函数 X2。例如，具有两个高度相关变量的重要性函数为
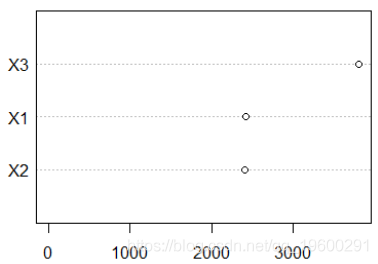
看起来 比其他两个X3 要 重要得多，但事实并非如此。只是模型无法在X1 和 之间选择 X2：有时会 X1 被选择，有时会被选择X2。我想我发现图形混乱，因为我可能会想到的 重要性 的 X1 恒定。考虑到其他变量的存在，我们已经掌握了每个变量的重要性。
实际上，我想到的是当我们考虑逐步过程时以及从集合中删除每个变量时得到的结果，
apply(IMP,1,mean)}在这里，如果我们使用与以前相同的代码，
我们得到以下图
plot(C,VI[2,],type="l",col="red")
lines(C,VI2[3,],col="blue")
lines(C,VI2[4,],col="purple")
删除时会显示紫线 X3 ：这是最差的模型。我们保持X1 和时 X3，我们得到了蓝线。而且这条线是恒定的：并不取决于 X2 （这在上一张图中，有 X2 确实会对X1重要性产生影响）。红线是移除后得到的 X1。关联为0时，它与紫色线相同，因此模型很差。关联度接近1时，与具有相同 X1，并且与蓝线相同。
然而，当我们拥有很多相关特征时，讨论特征的重要性并不是那么直观。
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
郑州地铁站点客流量预测：随机森林极限梯度提升回归器XGBoost
SPSS、Python员工满意度问卷调查激励保健理论研究：决策树、随机森林和AdaBoost|附代码数据
【视频讲解】CatBoost、LightGBM和随机森林的海域气田开发分类研究
