roc=function(s,print=FALSE){
Ps=(S<=s)*1
 
FP=sum((Ps==1)*(Y==0)/sum(Y==0)
 
TP=sum((Ps==1)*(Y==1)/sum(Y==1)
 
if(print==TRUE){
 
print(table(Observed=Y,Predicted=Ps))
 
 
vect=c(FP,TP)
 
names(vect)=c("FPR","TPR")
 

或R包

performance(prediction(S,Y),"tpr","fpr")

我们可以在这里同时绘制两个

 points(V[1,],V[2,])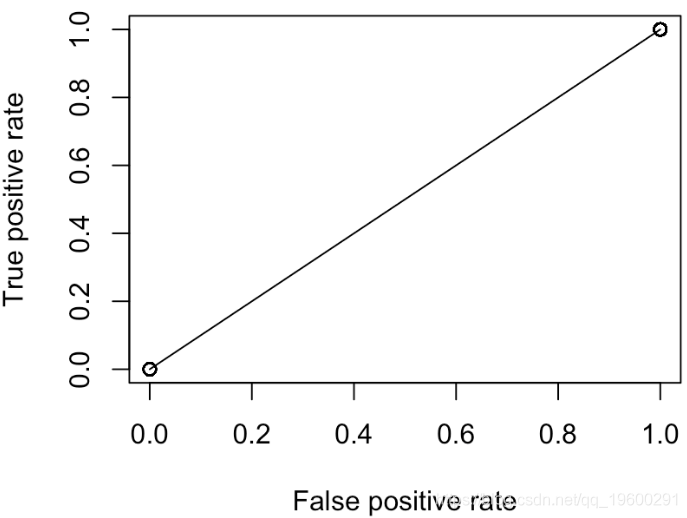

但是，我们这里只有两点：（0,0）和（1,1）。实际上，无论我们选择何种概率，都是这种情况

 
plot(performance(prediction(S,Y),"tpr","fpr"))
points(V[1,],V[2,])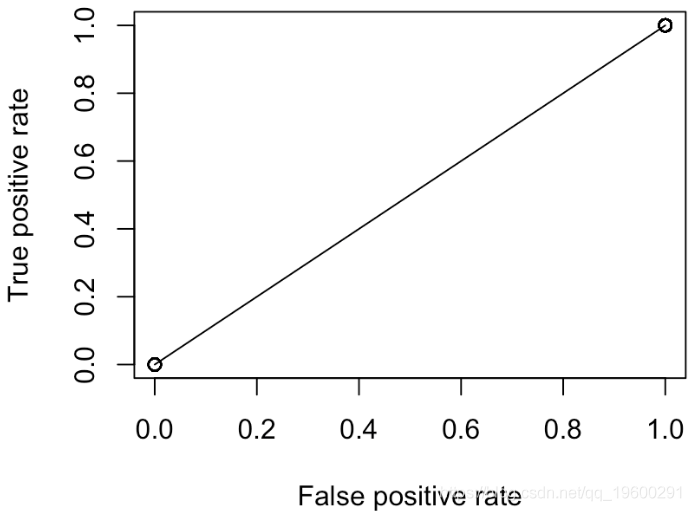

---

---

我们可以尝试另一种策略，例如“通过扔无偏硬币进行预测”。我们得到

 segments(0,0,1,1,col="light blue")

我们还可以尝试“随机分类器”，在其中我们随机选择分数

  S=runif(10)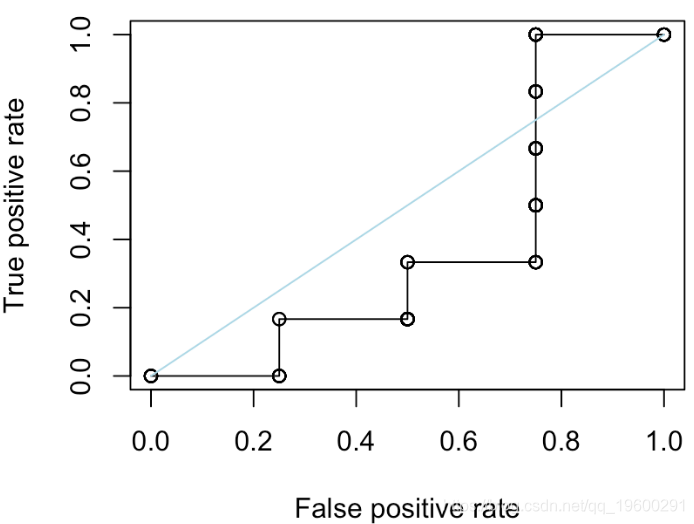

更进一步。我们考虑另一个函数来绘制ROC曲线

y=roc(x) 
lines(x,y,type="s",col="red")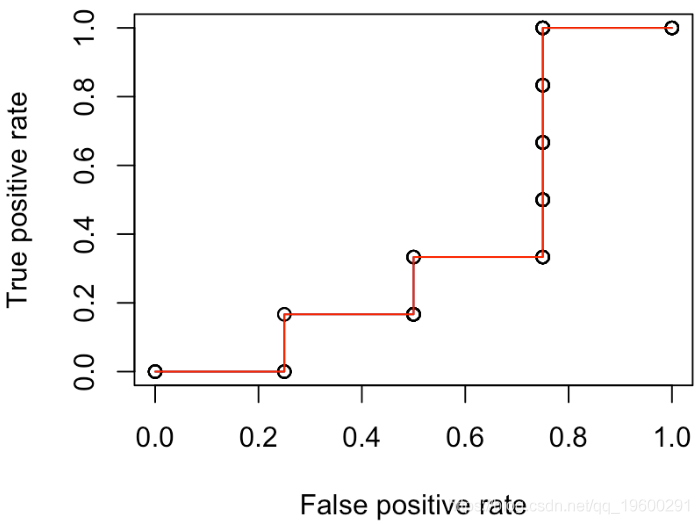

但是现在考虑随机选择的策略

 
for(i in 1:500){
S=runif(10)
V=Vectorize(roc.curve)(seq(0,1,length=251)
MY[i,]=roc_curve(x)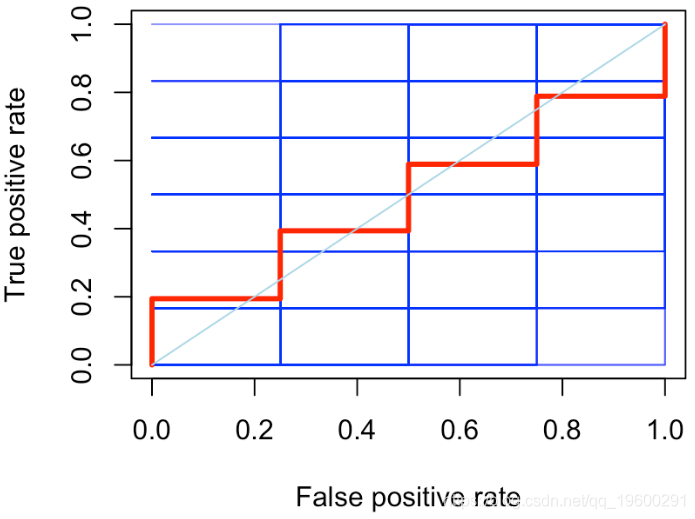

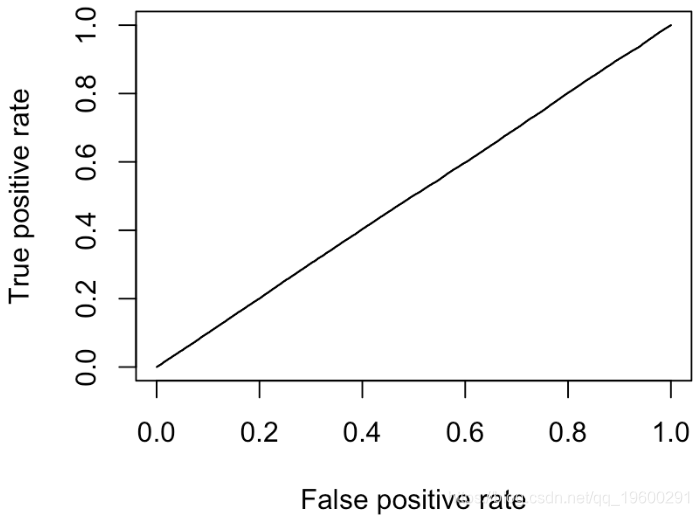
红线是所有随机分类器的平均值。它不是一条直线，我们观察到它在对角线周围的波动。

 
 
reg = glm(PRO~.,data=my,family=binomial(link = "logit"))
 
 
plot(performance(prediction(S,Y),"tpr","fpr"))
 
 
segments(0,0,1,1,col="light blue")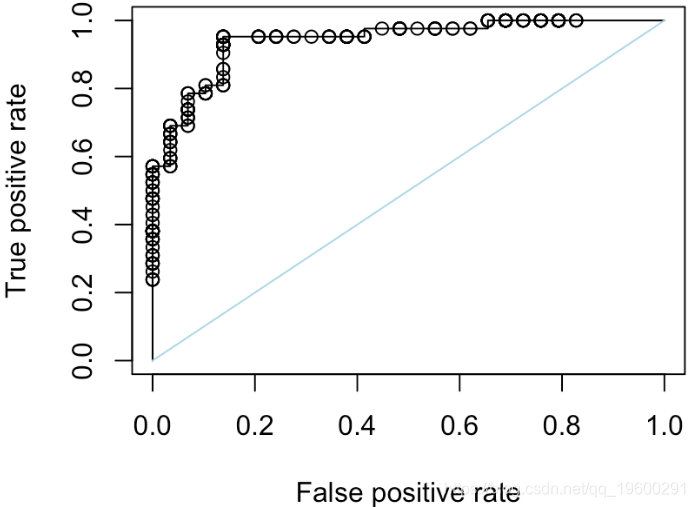

这是一个“随机分类器”，我们在单位区间上随机绘制分数

  segments(0,0,1,1,col="light blue")

如果我们重复500次，我们可以获得

 
for(i in 1:500){
S=runif(length(Y))
MY[i,]=roc(x)
}
lines(c(0,x),c(0,apply(MY,2,mean)),col="red",type="s",lwd=3)
segments(0,0,1,1,col="light blue")

因此，当我在单位区间上随机绘制分数时，就会得到对角线的结果。给定Y，我们可以绘制分数的两个经验累积分布函数

 
 
plot(f0,(0:(length(f0)-1))/(length(f0)-1))
 
lines(f1,(0:(length(f1)-1))/(length(f1)-1))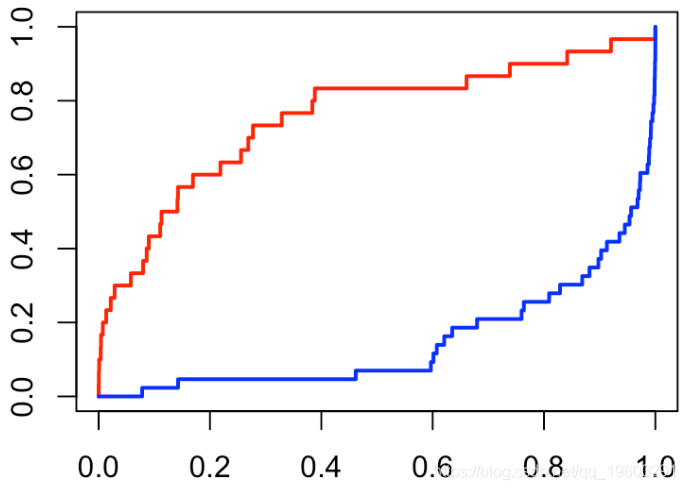

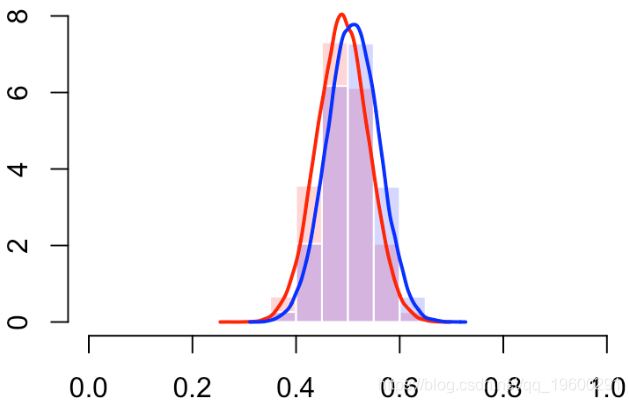
我们还可以使用直方图（或密度估计值）查看分数的分布

hist(S[Y==0],col=rgb(1,0,0,.2),
 probability=TRUE,breaks=(0:10)/10,border="white")
 

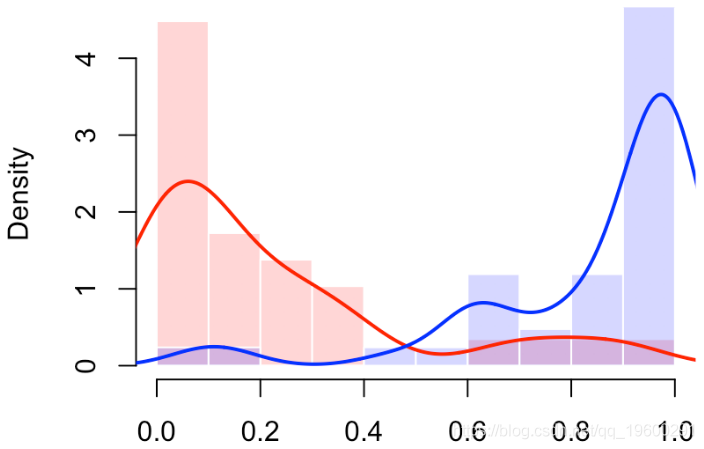
我们确实有一个“完美的分类器”（曲线靠近左上角）

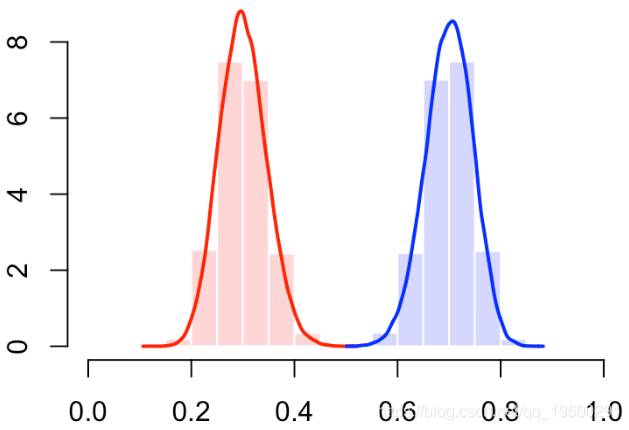
有错误。那应该是下面的情况

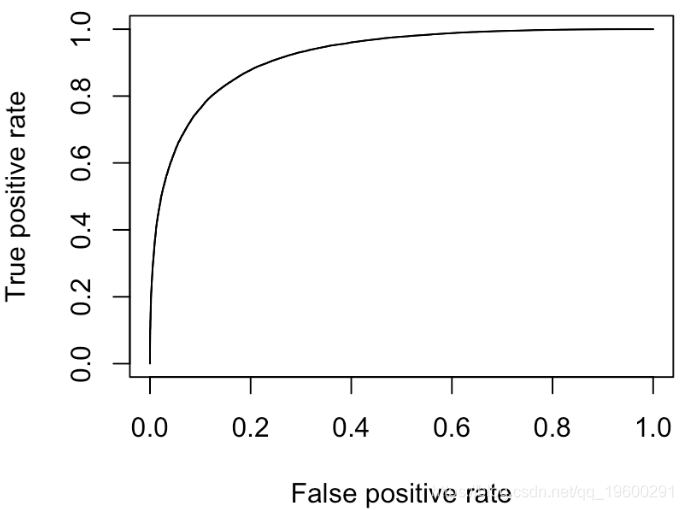
在10％的情况下，我们可能会分类错误

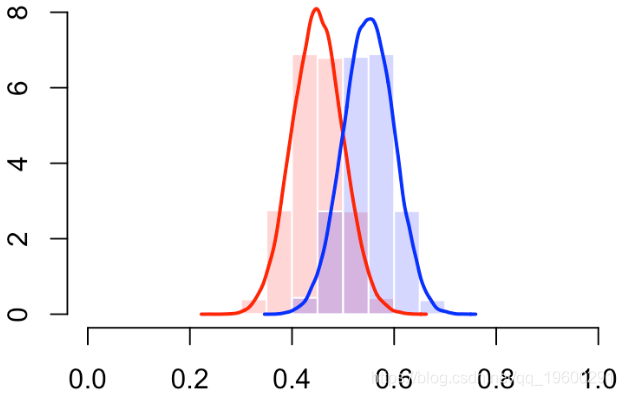
更多的错误分类

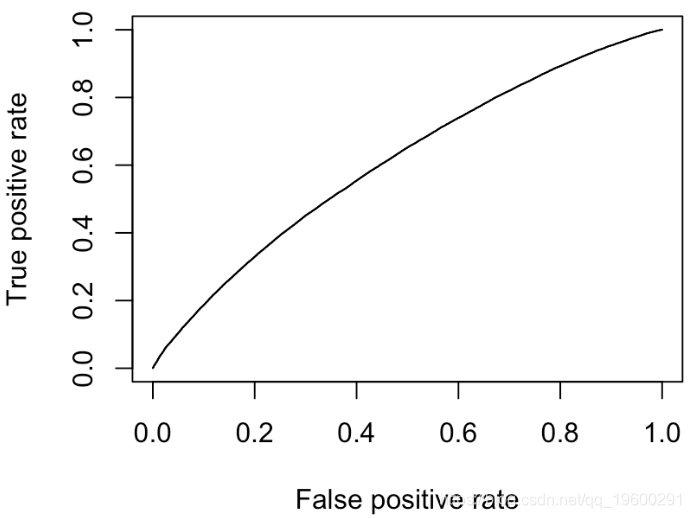
最终我们有对角线