为了找出影响价格波动的主要因素，我们使用逐步回归法来剔除一些对于应变量即把对价格影响很小的自变量剔除出我们的模型
我们分别把WTI Price Field 等自变量的名称改为x1，x2……
最后的突发事件需要用到哑变量，哑变量只需要2个即可，我们将其作为X49，X50，X51,三个参数并将它们的值”正影响”、”无影响”、”负影响”分别改为-1,0,1.。
可下载资源
经过R语言处理以后我们得到模型：
Y~x1 + x2 + x4 + x5 + x7 + x13 + x14 + x15 + x16 + x17 + x18 + x20 + x21 + x23 + x34 + x25 + x26 + x29 + x30 + x33 + x35 + x36 + x37 + x39 + x40 + x42 + x44 + x46 + x47 + x48 + x49 + x50
数据服从正态分布是许多统计方法的基本条件。下面介绍统计分析中验证数据正态性常用的三种方法。
1. 带正态分布概率密度曲线的直方图。 其基本原理是画出样本数据的频数分布（即直方图），然后该组数据的理论分布（密度曲线）进行比较，视觉上判断二者的吻合水平，以对数据的正态性做出初步评判。
当样本含量较小时，由于数据分组太少，可能会产生较大的偏差，对结果造成影响，因此该法适合用于大样本数据。
2. QQ plot。 以样本的分位数取值作为横坐标，其对应的正态分布理论分位数为纵坐标，画散点图，借以比较二者的拟合度。当数据与正态分布拟合较好时，图上的点会大致分布于一条直线上。
3. 利用假设检验。 用于正态性检验的假设检验类型，最常用的是D-W检验。D即 Kolmogorov-Smirnov检验法，该法计算D统计量。W即Shapiro-Wilk检验法，计算W统计量。
此外，偏度和峰度系数也常被用来作为评估数据正态性的参考。
峰度系数（Kurtosis）
当峰度 α >0时，表示分 布比正态分布更集中在平均数周围，分布呈尖峰状态；
α =0分布为正态分布；
α <0时，表示分布比正态分布更分散，分布呈低峰态
偏度系数(Skewness）
偏态系数的数值一般在0与±3之间，越接近0，分布的偏斜度越小；越接近±3，分布的偏斜度越大。
由此可得，影响较小的已经被剔除了。
Garch模型预测波动性
我们通过使用Garch模型来预测波动性，
先检验数据正态性，可以计算得出数据分布函数，QQ图，对数收益率序列折线图
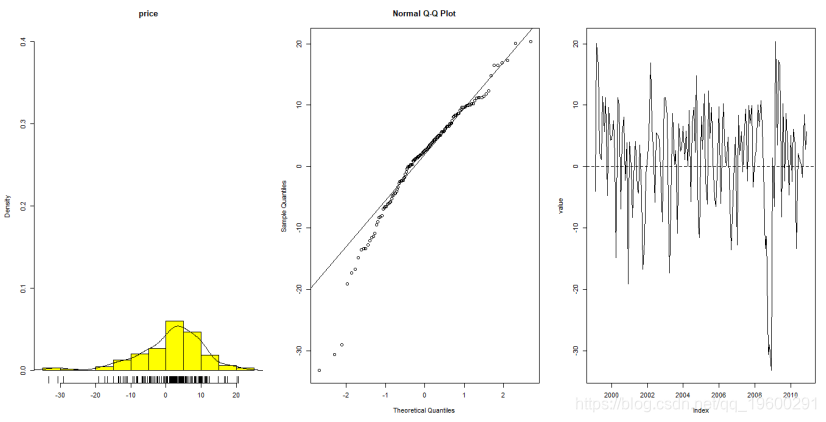
> shapiro.test(rlogdiffdata)
Shapiro-Wilk normality test
data: rlogdiffdata
W = 0.94315, p-value = 1.458e-05由QQ图以及p值可见，数据大致上符合正态分布。
最后用VaR曲线来进行预警剧烈波动。
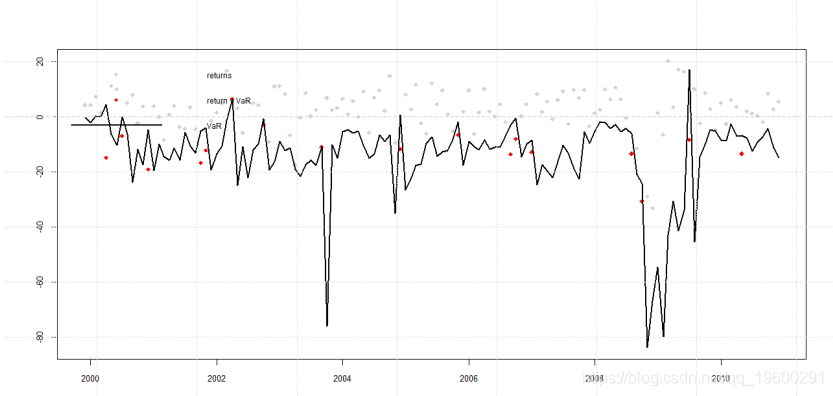
红色的点就是剧烈波动前的预警点。
强影响点分析
我们可以通过使用cook统计量来寻找强影响点，因此我们用R语言的influence.measures()函数来进行影响分析。
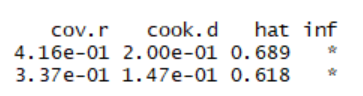
右侧带有*号的表示强影响点。
我们通过学生化残差来构造F检验，最终得到t检验，以此来检测异常点。通过
stdres<-rstudent(lm.sol)来得到学生化残差，然后通过公式
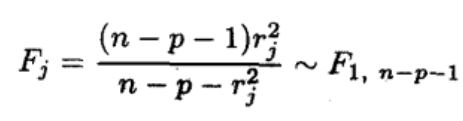
来计算Fj，并且最终转化为tj，
t=sqrt((144-51-1)*stdres^2/(144-51-stdres^2))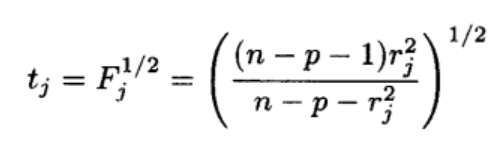
最后我们可以检查，如果
则它为异常点。
R语言执行
res<-t>abs(qt(.025, df=92)) 可以直接得到大于对应t值的布尔值。
值为True的则可能为异常点。
预测
我们使用了HoltWinters来进行预测我们的价格区间
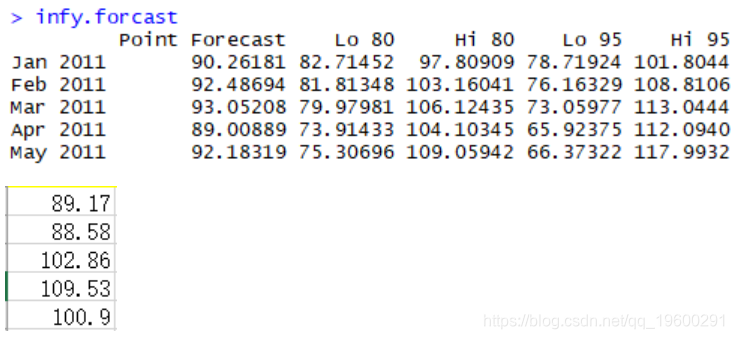
真实值基本都在预测的范围内，但是想要净赚预测还是比较困难的。
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据：旅游市场差异、价格预测
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
