最近我们被客户要求撰写关于线性混合效应模型的研究报告，包括一些图形和统计输出。线性混合效应模型与我们已经知道的线性模型有什么不同？
线性混合模型（有时被称为 “多层次模型 “或 “层次模型”，取决于上下文）是一种回归模型，它同时考虑了（1）被感兴趣的自变量（如lm()）所解释的变化–固定效应，以及（2）不被感兴趣的自变量解释的变化–随机效应。
可下载资源
由于该模型包括固定效应和随机效应的混合，所以被称为混合模型。这些随机效应本质上赋予误差项ϵ结构。
多层线性模型（Hierarchical Linear Model，HLM），也叫多水平模型（Multilevel Model，MLM），是社会科学常用的高级统计方法之一，它在不同领域也有一些近义词或衍生模型：
线性混合模型（Linear Mixed Model）
混合效应模型（Mixed Effects Model）
随机效应模型（Random Effects Model）
随机系数模型（Random Coefficients Model）
方差成分模型（Variance Components Model）
增长曲线模型（Growth Curve Model）
……
1 / 什么是HLM
子曾经曰过：“HLM是众多统计方法的「幕后主谋」。”什么意思呢？一般我们收集完数据之后会做什么分析？做实验的人会说：方差分析（ANOVA）；做调查的人会说：多元回归（multivariate regression）；做文献综述的人会说：元分析（meta-analysis）……但其实，这一切都可以视为HLM的特例：
t检验是ANOVA的一个特例（自变量只有两水平）
ANOVA是回归分析的一个特例（自变量为分类变量）
回归分析的实质是一般线性模型GLM（其推广则是广义线性模型）
GLM是HLM的一个特例（只有Level 1）
元分析可以视为只有组间模型的HLM（只有Level 2）
简而言之：回归分析是几乎所有统计模型的基础，而回归分析的最一般形式则可以归为多层线性模型HLM。
当然，除去上面这些HLM的特例，HLM本身关注的焦点其实是“多层嵌套数据”。
HLM会把多层嵌套结构数据在因变量上的总方差进行分解：
总方差 = 组内方差（Level 1）+ 组间方差（Level 2）
我们既可以用R语言lme4、lmerTest包的lmer函数，也可以用SPSS的MIXED语句进行建模：
# R语言 - 固定斜率:model = lmer(GPA ~ IQ + (1|School), data=data)# SPSS - 固定斜率:MIXED GPA WITH IQ
/METHOD=REML
/PRINT=DESCRIPTIVES SOLUTION TESTCOV
/FIXED=IQ | SSTYPE(3)
/RANDOM=INTERCEPT | SUBJECT(School) COVTYPE(VC).
或者可以设置IQ为随机斜率（即理论上假定IQ与GPA之间的关系在不同学校是不一样的）：
# R语言 - 随机斜率:model = lmer(GPA ~ IQ + (IQ|School), data=data)# SPSS - 随机斜率:MIXED GPA WITH IQ
/METHOD=REML
/PRINT=DESCRIPTIVES SOLUTION TESTCOV
/FIXED=IQ | SSTYPE(3)
/RANDOM=INTERCEPT IQ | SUBJECT(School) COVTYPE(UN).
我们来看HLM的一般式：
Level 1（组内/个体水平，或重复测量/追踪设计中的时间水平；p个自变量，i个样本量）：
Level 2（组间/群体水平，或重复测量/追踪设计中的个体水平；q个自变量，j个样本量）：
以上就是关于HLM的入门级科普。我不确定是不是所有读者都对HLM有足够的了解，因为很多同学其实是没有接触过HLM的，我自己也是2017年暑假才开始学习HLM。不仅如此，一些实验取向、认知取向的同学甚至会怀疑回归分析的意义，因为在他们的研究中，t检验和ANOVA就足够用了——而这些分析的本质其实都是回归分析，回归分析的更一般形式则是HLM。
另外，也有不少同学把“多层线性模型”与“分层/逐步多元回归”搞混淆——请注意：
-
多层线性模型HLM解决的是多层嵌套结构数据（落脚点是数据结构）
-
分层/逐步多元回归本身是普通的回归分析，解决的是不同自变量的重要性的优先程度（落脚点是变量重要性）
2 / HLM的自由度计算问题
前面这些都只是铺垫，因为下面的内容才是重点。我们来谈谈HLM的自由度计算问题。
自由度（degree of freedom, df），简单来说就是“能够独立变化的数据量”。比如一组有N个数据的样本，其总体平均值是确定的，那么在参数估计中，我们说它的自由度是N – 1，这里的1代表已经确定了的均值，也就是说无论你的数据怎么变，只要给我N – 1个数，我就能知道剩下的那个数是几，因为均值已经确定了。
而在普通的回归分析中，同样道理，截距相当于一个已经确定了的均值，是我们要估计的一个参数，并且每增加一个自变量，都会相应增加一个回归系数，这些回归系数也是我们要估计的参数，也视为确定值，因此剩下的那些不确定的、能够独立变化的数据的个数就是自由度，主要用于假设检验（对回归系数的检验：t = b/SE，服从df = N – k的t分布，其中N为总样本量，k为所有的参数个数，截距也占一个参数）。
一言以蔽之：
df （能够独立变化的数据量）= N（总数据量）– k（待估计的参数个数 [包括截距]）
事实上任何一个回归方程都有且仅有一个截距，就好比任何一组数据都有且仅有一个平均值，所以很多时候上面这个表达式也可以用“自变量/预测变量”的个数来表示：
df = N – k = N – p – 1（p表示自变量/预测变量的个数，1表示截距这个参数）
然而，这么一目了然的事情在HLM里面却是一件比较复杂的议题，因为前面我们已经看到，HLM的回归方程不止一个，不仅有Level 1的一个方程，还有Level 2的一系列以Level 1的每个参数（包括截距和斜率）为因变量建立的方程，因此不同的回归系数因其对应的变量有不同的性质（或者说在HLM中所处的不同层级），其自由度也不尽相同。
固定效应和随机效应的定义可能会有所不同，所以要注意你在文献中的解释。
但是，对于大多数目的来说，如果从所有感兴趣的层面收集了数据，你可以把一个变量视为固定效应因素（例如 性别：男/女，条件：易/中/难，剂量：低/高），如果变量有一堆可能的水平，但你只对一个随机的集合（如受试者、刺激物、教室）进行采样，尽管这些样本会有一些特异性，但你一般不会关心它们，目的是对更广泛的人群进行概括（如所有的人、所有的场景、所有的教室）。
例子
比方说，你对语言感兴趣，更确切地说，是对声音的高低与礼貌态度的关系感兴趣。你要求你的受试者对假设的场景（IV，受试者内部）做出反应，这些场景要么是需要礼貌态度的正式场合（例如，给教授一个迟到的借口），要么是比较非正式的场合（例如，向朋友解释你为什么迟到），并测量他们的音调（DV）。每个受试者都会得到一份所有场景的清单，因此每个受试者都会给出多个礼貌态度的或非正式的回答。你还注意到每个受试者的性别（IV，受试者之间），因为这是对声调的另一个重要影响。
在迄今为止我们所看到的线性模型中，我们将建立这样的模型。
声调=礼貌态度+性别+ϵ
其中最后一项是我们的误差项。这个误差项代表了由于我们无法在实验中控制的 “随机 “因素而导致的与我们预测的偏差。
对于这种数据，由于每个受试者都给出了多个反应（”重复测量 “设计），我们可以看到，这将违反线性建模中重要的独立性假设：同一受试者的多个反应不能被视为彼此独立。在我们的方案中，每个人的声调都略有不同，这将成为影响同一受试者所有反应的特异性因素，从而使这些不同的反应相互依赖（相关）而非独立。
随机效应
我们要处理这种情况的方法是为主体添加一个随机效应。这使我们能够通过为每个受试者假设不同的 “基准 “音高值来解决这种非独立性。因此，受试者1在不同的话语中可能有233赫兹的平均声调，而受试者2可能有210赫兹的平均声调。在我们的模型中，我们通过对受试者的随机效应来解释这些声调的个体差异。
我们将一些数据为例进行分析。
table(subject)
把数据可视化。
qplot(condition, pitch, facets = . ~ subject)
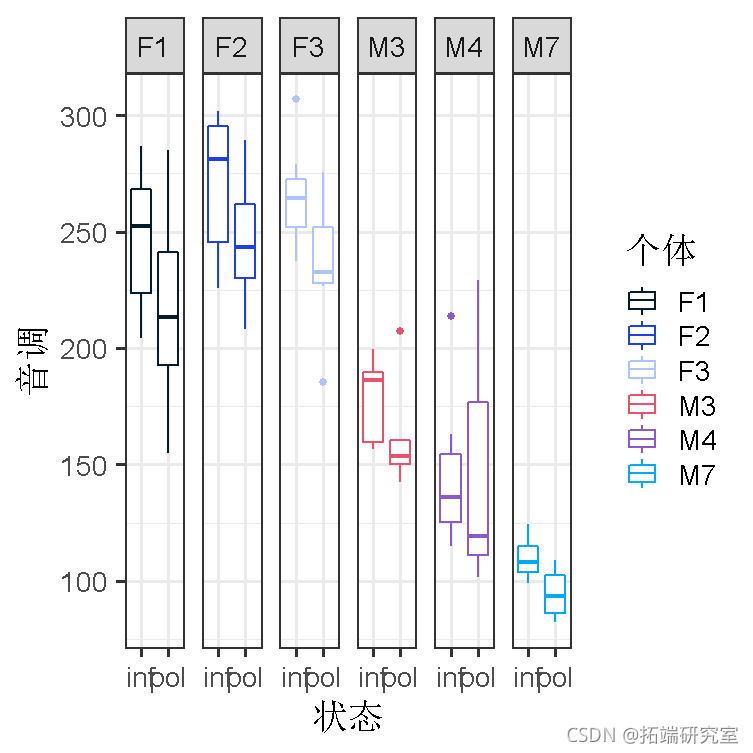
受试者 “F#”为女性受试者。对象 “M#”是男性对象。你马上就会发现，男性的声音比女性低（这是可以预期的）。但除此之外，在男性和女性群体中，你会看到很多个体差异，一些人的性别值相对较高，而另一些人的性别值相对较低。
来自同一主体的样本的相关性
另一种说法是，在受试者内部，不同条件下的音高存在着相关性。让我们把它形象化。
用随机截距对个体平均值进行建模
我们可以通过为每个参与者假设不同的随机截距来建立这些个体差异的模型；每个参与者都被分配了不同的截距值（即不同的平均声调），而混合模型基本上是为你估计这些截距。
随时关注您喜欢的主题
回过头来看我们的模型，我们以前的公式是。
声调=截距+礼貌+性别+ϵ
我们更新后的公式是这样的。
声调=截距+礼貌+性别+(1|个体)+ϵ
“(1|subject) “是随机截距的R语法。这句话的意思是 “假设每个主体的截距都不同”……而 “1 “代表这里的截距。你可以认为这个公式是告诉你的模型，它应该期望每个受试者会有多个反应，而这些反应将取决于每个受试者的基准水平。这就有效地解决了因同一受试者有多个反应而产生的非独立性问题。
请注意，该公式仍然包含一个一般误差项ϵ。这是必要的，因为即使我们考虑到了每个主体的变化，同一主体的不同音高之间仍然会存在 “随机 “差异。
对不同条件下的不同参与者的平均值有一个概念。
aggregate(pitch ~ subject, FUN = "mean")
现在用lmer() ，我们可以估计每个参与者的平均值。为了做到这一点，我们将为每个受试者包含一个随机截距，然后看一下估计的截距。
coef(lmer(pitch ~ (1 | subject))
#固定效应+随机效应的主体 \['（截距）'\] + subject
请注意，估计值与实际平均音高相当接近，我们可以看到，各受试者的实际平均音高是估计值（Intercept），而各受试者平均音高的标准差是随机效应的标准差（Std.Dev）。
# 使用原始数据 mean
## \[1\] 193
sd
## \[1\] 63.47
# 使用每个子项目的估计截距 mean(subject\[1\]\[,'(Intercept)'\])
## \[1\] 193
sd
## \[1\] 62.4
# 这也是模型输出中的总结 summary(res1)
由于我们预测假设状态的条件（”非正式 “与 “礼貌态度”）会影响音调（也许在非正式状态下音调会更高）
包括固定效应
lmer(音调~礼貌+性别+(1|个体))
，此外还有受试者的性别（女性的音调可能会更高），让我们把这些条件纳入模型，同时也考虑到每个受试者的随机截距（让截距因受试者而异）。
音调j=截距+截距j+状态+性别
音调 A=截距+A截距的变动〔_Intercept_ _Shift_〕+状态+性别
ggplot(x=condition, y=mean)
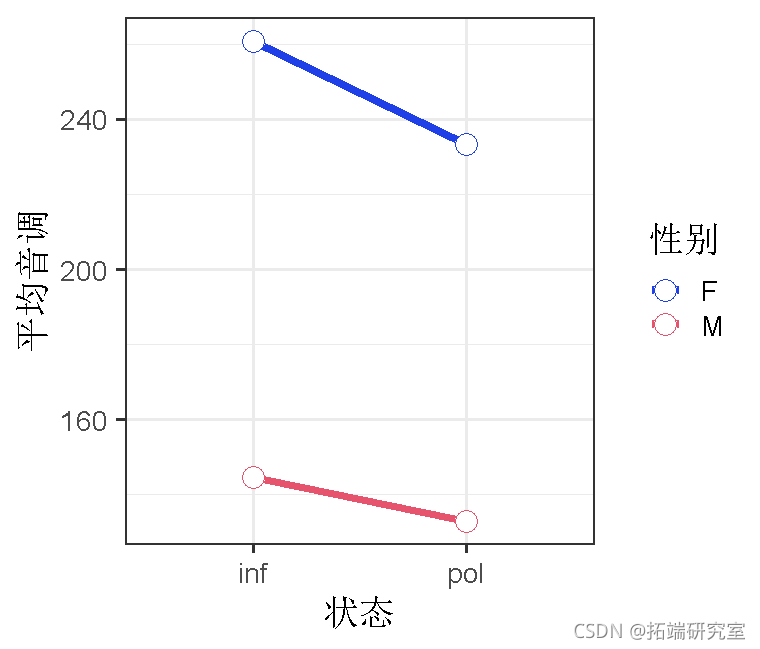
在这里，我们还将对比状态和性别，这样我们就可以看到条件在女性和男性之间的 “平均值 “的影响，以及性别在 “非正式 “和 “不礼貌 “之间的平均值的影响。
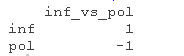
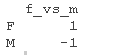
可以看到，我们的平均音调是192.88，非正式状态的音调比礼貌状态的音调高，b=9.71，t=3.03，女性的音调比男性高，b=54.10，t=5.14。我们可以使用一个经验法则，如果t大于2，就可能是显著的。
更多模型信息
我们可以用许多不同类型的信息来评估模型。在比较模型的时候，这些信息可能很有用 一个有用的衡量标准是AIC，即偏差+2∗(p+1)，其中p是模型中的参数数量（这里，我们将参数分解，所以1是估计的残差，p是所有其他参数，例如，固定效应系数+估计的随机效应的方差等）。较低的AIC比较好，因为较高的偏差意味着模型不能很好地拟合数据。由于AIC随着p的增加而增加，所以AIC会因为更多的参数而受到惩罚。
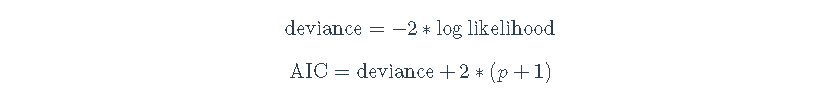
deviance = -2*logLikelihood; deviance
## \[1\] 789.5
# 用手计算AIC p = 4 # 参数 = 3（固定效应）+1（随机效应 deviance + 2*(p+1) # 总参数 = 4 + 1 用于估计残差
## \[1\] 799.5
AIC(res2)
## \[1\] 799.5
提取所有系数
ggplot(aes(x=factor(subject), y=mean_pitch))
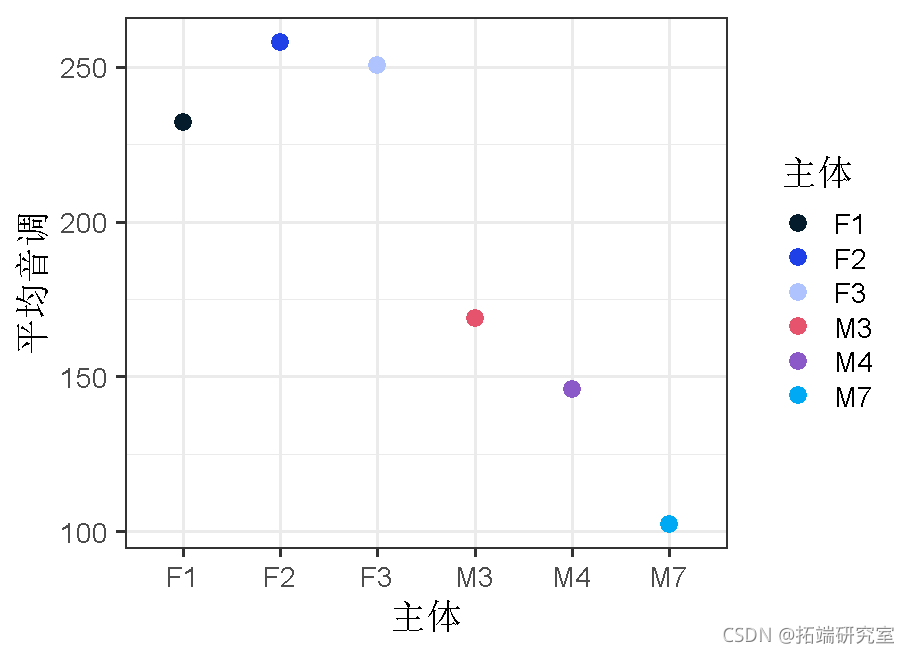
coef(res2)
在这里，我们可以看到，这个模型为每个受试者产生了一个单独的截距，此外还有一个参数估计值/斜率的条件和性别，在各受试者中是恒定的。从这里，我们可以尝试根据这些系数来估计一个给定样本的平均音高 。例如，让我们尝试用他们估计的截距和作为女性的影响来估计受试者F1的平均数（x¯=232.0357）。
179.3003 + 0*(9.7) + 1*(54.10244)
## \[1\] 233.4
相当接近
现在是M3（x¯=168.9786）:
220.3196 + 0*(9.7) + -1*(54.10244)
## \[1\] 166.2
还不错
随机斜率
在上面的模型中，我们假设礼貌态度的影响对所有被试都是一样的，因此，礼貌态度的系数是一个。然而，礼貌态度的影响对于不同的受试者主体可能是不同的；也就是说，可能存在着受试者主体礼貌态度的相互作用。例如，我们可以预期，有些人在有需要礼仪的场景下更有礼貌，有些人则不那么有礼貌。因此，我们需要的是一个随机斜率模型，在这个模型中，不仅允许主体有不同的截距，而且还允许它们对礼貌的影响有不同的斜率（即状态对音调的不同影响）。
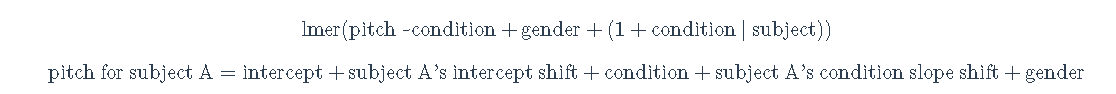
让我们开始将数据可视化。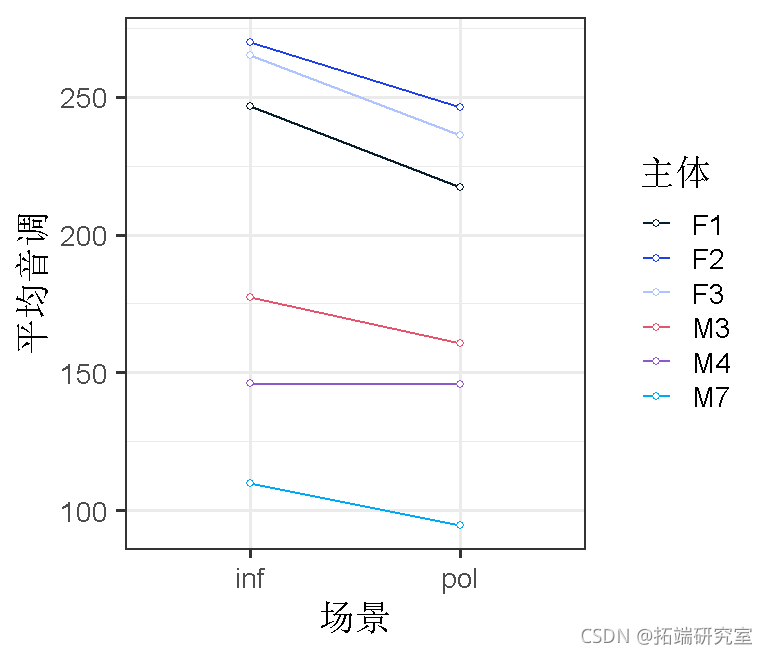
根据这幅图，看起来各受试者的斜率是否很不稳定？
现在加入随机斜率。
coef(res3)
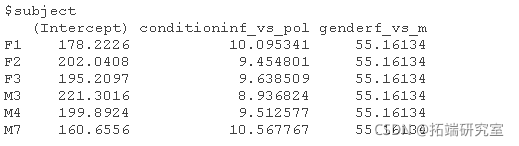
anova(res2, res3, refit=FALSE)
增加每个受试者的随机斜率又占用了2个自由度，并没有明显改善模型拟合，χ2(2)=0.024,P=0.99。注意df=2，因为我们同时加入了斜率方差和截距与斜率之间的相关关系。看一下AIC值，更复杂的模型的AIC值更高，所以我们想用不太复杂（更简明）的模型。如果我们看一下估计的斜率，我们可以看到它们在不同的样本中是非常相似的。所以，我们不需要在模型中加入条件的随机斜率。
然而，其他人会认为，我们应该保持我们的模型最全面，并且应该包括随机斜率，即使它们没有改善模型!
测试显著性
虽然对是否应该获得lmer()模型的p值有一些争论（例如，这个；大多数争论围绕着如何计算dfs），但你可以使用{lmerTest}包获得df的近似值（以及因此获得p值）。
获取P值
summary(res3b)
将模型输出与SS/Kenward-Roger appox进行比较
anova
anova(res2b)
模型比较
另一方面，有些人认为，用似然比检验进行模型比较是检验一个参数是否显著的更好方法。也就是说，如果在你的模型中加入该参数能显著提高模型的拟合度，那么该参数就应该被纳入模型中。
似然比检验本质上告诉我们，数据在更复杂模型下的可能性比在简单模型下的可能性大多少（这些模型需要嵌套！）：
D的分布大约是χ2，自由度为df2-df1。我们要么 “手动 “做这个计算，要么就直接使用anova()函数!
anova(res4, res4b)
# 手动计算 dev0 <- -2*logLik(res4) # 较简单的偏差模型 devdiff <- (dev0-dev1) # 偏差差值 dfdiff # 参数的差异（使用dfs）。
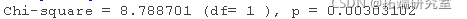
在这里，我们比较了两个嵌套模型，一个没有条件，另一个有条件。通过模型比较，我们得出结论，在我们的模型中加入条件是有必要的，因为它明显改善了模型的拟合，χ2(1)=8.79,P<0.01。
REML与ML
让我们从一个统计模型开始，指定（i）固定效应和（ii）各种随机效应的正态分布的变异和协方差。
- 在ML（最大似然）估计中，我们计算上述（i）和（ii）组中任意选择的参数值的数据的对数（似然）（LL）。然后，我们寻找能使L最大化（或最小化-L）的参数值。这些最佳参数值被称为ML参数估计值。L的最大值（-2倍）被称为模型的偏差。对于某些目的，如描述数据，我们关注ML参数估计值；对于其他目的，如模型比较，我们关注偏差。在比较固定效应不同的模型时，你应该使用ML，而且你必须包括lmer(, REML=FALSE)。此外，如果你要比较一个lm()和lmer()模型（即测试是否有必要使用任何随机效应），你也应该使用ML估计。
- 在REML（REstricted ML）估计中，我们的主要兴趣是估计随机效应，而不是固定效应。想象一下，我们通过将上面第(i)组中的固定效应参数设置为某些合理的值来限制我们的参数空间。在这个限制的空间里，我们寻找集(ii)中的随机效应参数值，使数据的LL值最大化；同时注意LL值的最大值。然后多次重复这个过程。然后对固定效应参数值、随机效应参数的估计值和LL的最大值进行平均。这种平均法可以得到REML参数估计值和REML偏差值。因为这个过程对固定效应参数的关注度很低，所以它不应该被用来比较固定效应结构不同的模型。你应该在比较随机效应不同的模型时使用这个方法。要做到这一点，你应该养成在运行模型比较时包括lmer(, REML=TRUE)，并使用anova(, refit=FALSE)的习惯。
例子
测试随机效应是否有必要
dev1 <- -2*logLik(res5) dev0 <- -2*logLik(res5b) devdiff <- as.numeric(dev0-dev1); devdiff
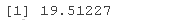
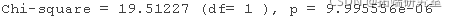
# 比较AICs AIC(res5b, res5)
AICtab(res5b, res5) # AIC
用anova直接比较lm和nlme模型
看起来，是的，纳入受试者的随机截距是有道理的，χ2(1) = 19.51, P < 0.001.
在这里，χ2分布并不总是一个很好的无效分布的近似值（在测试一些随机效应时过于保守，而在测试一些固定效应时不够保守）。
场景效应
不同的场景可能会引起不同的 “音调 “值；因此，在不同的受试者之间，甚至在一个受试者内部，在礼貌和非正式的状态下，特定场景的音调可能是相关的。我们可以把这作为一个随机效应的模型。
ggplot(d, aes(x=scenario, y=pitch)
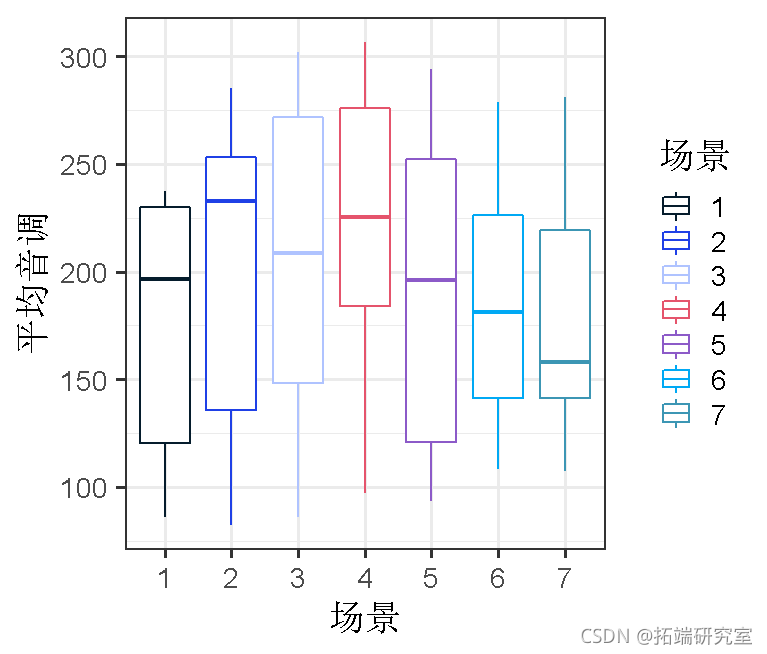
anova
coef(res4)
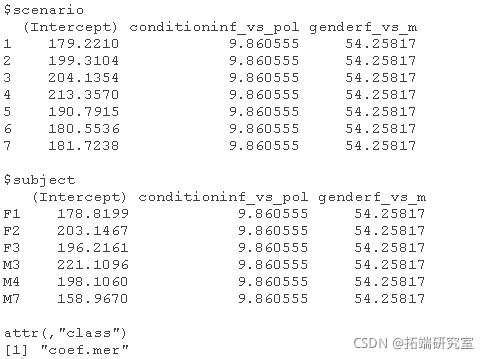
与受试者的随机截距相似，现在我们有了每种场景下的平均音高水平。
那么，每个场景的斜率变化呢？
ggplot(byscenario, aes(x=condition, y=pitch))
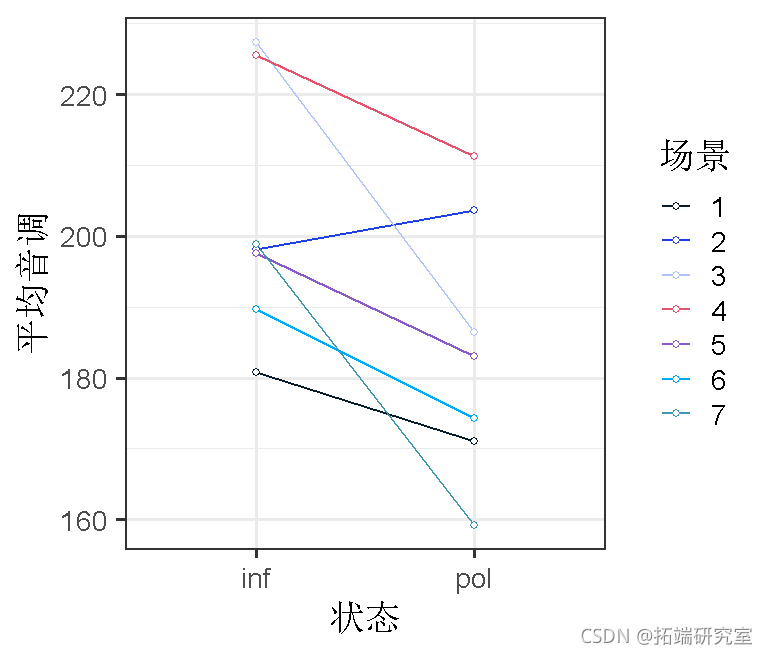
anova
没有改善模型。这说明我们的方案在非正式和礼貌状态下的差异方面可能是相似的。
混合模型说明
这里有几件重要的事情要讲。你可能会问 “我应该指定哪些随机斜率？” 甚至是 “随机斜率到底有没有必要？”
从概念上讲，将随机斜率和随机截距一起包括进来是非常有意义的。毕竟，你可以认为人们对实验操纵的反应不同！同样，你可以认为人们对实验操纵的反应不同。同样，你总是可以认为，实验操纵的效果对实验中的所有项目都不一样。
在上述模型中，我们的整个研究关键在于说明有关礼貌的东西。我们对性别差异不感兴趣，但它们是很值得控制的。这就是为什么我们对礼貌态度的影响有随机斜率（按被试和项目），而不是性别。换句话说，在礼貌态度对音调的影响方面，我们只模拟了按主体和按项目的变化。
在线性模型背景下讨论的一切都直接适用于混合模型。因此，你还必须担心共线性和异常值。你还得担心同方差（方差相等）和潜在的正态性缺失问题。
独立性，作为最重要的假设，需要一个特殊的词。我们转向混合模型而不是仅仅使用线性模型的主要原因之一是为了解决我们数据中的非依赖性。然而，混合模型仍然可以违反独立性。如果你缺少重要的固定或随机效应。因此，例如，如果我们用一个不包括随机效应 “主体 “的模型来分析我们的数据，那么我们的模型就不会 “知道 “每个主体有多个反应。这就相当于违反了独立假设。因此，要仔细选择你的固定效应和随机效应，解决非独立性问题。
其他一些说明。
如果你的因变量是…
- 连续：使用混合效应的线性回归模型
- 二元：使用混合效应的Logistic回归模型
函数lmer用于拟合线性混合模型，函数glmer用于拟合广义（非高斯）线性混合模型。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
R语言MCMC的lme4二元对数Logistic逻辑回归混合效应模型分析吸烟、喝酒和赌博影响数据
python可视化探索新冠疫情病毒与失业率是否存在线性关系
