本文，我通过两个种群生态学家可能感兴趣的例子来说明使用“JAGS”来模拟数据：首先是线性回归，其次是估计动物存活率（公式化为状态空间模型）。
最近，我一直在努力模拟来自复杂分层模型的数据。我现在正在使用 JAGS。
模拟数据 JAGS 很方便，因为你可以使用（几乎）相同的代码进行模拟和推理，并且你可以在相同的环境（即JAGS）中进行模拟研究（偏差、精度、区间覆盖 ）。
可下载资源
线性回归示例
我们首先加载本教程所需的包：
library(R2jags)
然后直接切入正题，让我们从线性回归模型生成数据。使用一个 data 块，并将参数作为数据传递。
data{
# 似然函数:
for (i in 1:N){
y\[i\] ~ # tau是精度（1/方差）。
}
这里， alpha 和 beta 是截距和斜率、 tau 方差的精度或倒数、 y 因变量和 x 解释变量。
我们为用作数据的模型参数选择一些值：
# 模拟的参数 N # 样本 x <- 1:N # 预测因子 alpha # 截距 beta # 斜率 sigma# 残差sd 1/(sigma*sigma) # 精度 # 在模拟步骤中，参数被当作数据处理
现在运行 JAGS; 请注意，我们监控因变量而不是参数，就像我们在进行标准推理时所做的那样：
# 运行结果 out
输出有点乱，需要适当格式化：
# 重新格式化输出 mcmc(out)
dim
dat
现在让我们将我们用来模拟的模型拟合到我们刚刚生成的数据中。不再赘述，假设读者熟悉 JAGS 线性回归。
# 用BUGS语言指定模型
model <-
for (i in 1:N){
y\[i\] ~ dnorm(mu\[i\], tau) # tau是精度(1/方差)
alpha 截距
beta # 斜率
sigma # 标准差
# 数据
dta <- list(y = dt, N = length(at), x = x)
# 初始值
inits
# MCMC设置
ni <- 10000
# 从R中调用JAGS
jags()
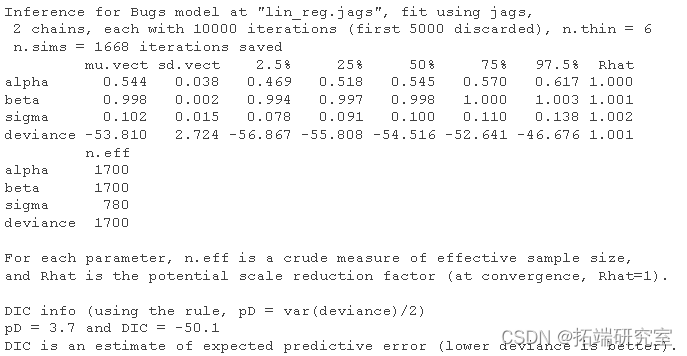
让我们看看结果并与我们用来模拟数据的参数进行比较（见上文）：
# 总结后验 print(res)
随时关注您喜欢的主题
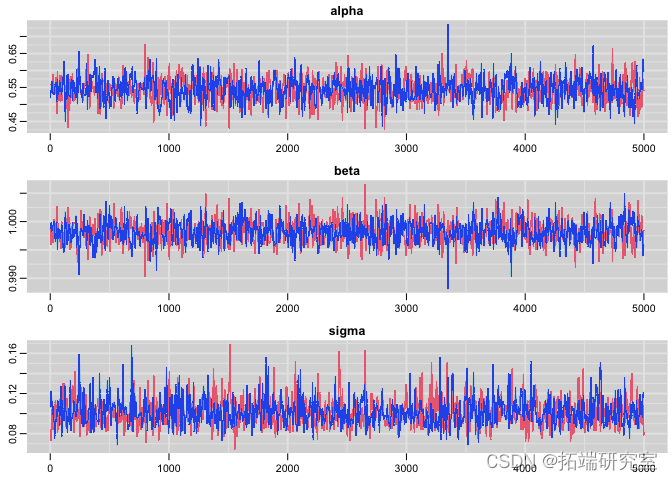
检查收敛：
# 追踪图 plot(res)
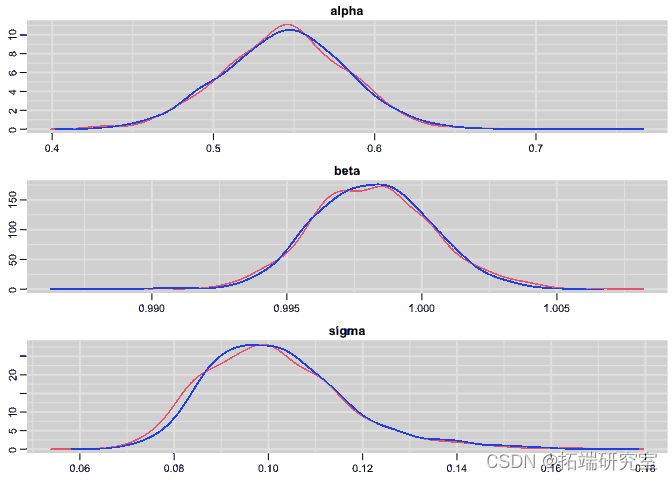
绘制回归参数和残差标准差的后验分布：
# 后验分布 plot(res)
模拟示例
我现在说明如何使用 JAGS 来模拟来自具有恒定生存和重新捕获概率的模型的数据。我假设读者熟悉这个模型及其作为状态空间模型的公式。
让我们模拟一下！
# 恒定的生存和重新捕获概率
for (i in 1:nd){
for (t in f:(on-1)){
#概率
for (i in 1:nid){
# 定义潜伏状态和第一次捕获时的观察值
z\[i,f\[i\] <- 1
mu2\[i,1\] <- 1 * z\[i,f\[i\] # 在第一次捕获时检测为1（"以第一次捕获为条件"）。
# 然后处理以后的情况
for (t in (f\[i\]+1):non){
# 状态进程
mu1\[i,t\] <- phi * z
# 观察过程
mu2\[i,t\] <- p * z
# 用于模拟的参数 n = 100 # 个体的数量 meanhi <- 0.8 # 存活率 meap <- 0.6 # 重捕率 data<-list
让我们为参数选择一些值并将它们存储在数据列表中：
现在运行 JAGS：
out
格式化输出：
as.mcmc(out)
head(dat)
我只监测了检测和非检测，但也可以获得状态的模拟值，即个人在每种情况下是生是死。你只需要修改对JAGS 的调用 monitor=c("y","x") 并相应地修改输出。
现在我们将 Cormack-Jolly-Seber (CJS) 模型拟合到我们刚刚模拟的数据中，假设参数不变：
# 倾向性和约束
for (i in 1:nd){
for (t in f\[i\]:(nn-1)){
mehi ~ dunif(0, 1) # 平均生存率的先验值
Me ~ dunif(0, 1) # 平均重捕的先验值
# 概率
for (i in 1:nd){
# 定义第一次捕获时的潜伏状态
z\[i\]\] <- 1
for (t in (f\[i\]+1):nions){
# 状态过程
z\[i,t\] ~ dbern(mu1\[i,t\])
# 观察过程
y\[i,t\] ~ dbern(mu2\[i,t\])
准备数据：
# 标记的场合的向量 gerst <- function(x) min(which(x!=0)) # 数据 jagta
# 初始值
for (i in 1:dim\]){
min(which(ch\[i,\]==1))
max(which(ch\[i,\]==1))
function(){list(meaphi, mep , z ) }
我们想对生存和重新捕获的概率进行推断：
标准 MCMC 设置：
ni <- 10000
准备运行 JAGS！
# 从R中调用JAGS jags(nin = nb, woy = getwd() )
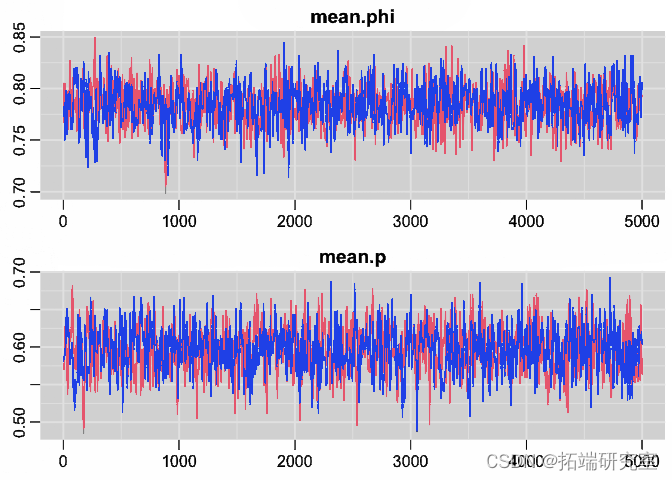
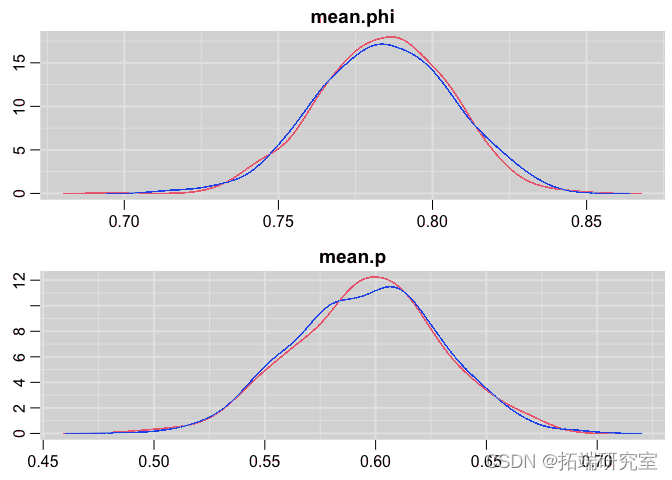
总结后验并与我们用来模拟数据的值进行比较：
print(cj3)
非常接近！
跟踪图
trplot
后验分布图
denplot
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
R语言极值分析：GEV与GPD模型与MCMC的海洋观测数据极值模拟可视化研究
Python预测体重变化：决策树、tf神经网络、随机森林、梯度提升树、线性回归可视化分析吸烟与健康调查数据
