
此示例显示如何用R语言进行特征选择——逐步回归
选择在满足一些明确的客观标准时做得最好的预测变量的子集,例如具有最大R2值或最小MSE, Cp或AIC。
可下载资源
变量选择方法
所有可能的回归
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
ols_all_subset(model)
## # A tibble: 15 x 6
## Index N Predictors `R-Square` `Adj. R-Square` `Mallow's Cp`
##
## 1 1 1 wt 0.75283 0.74459 12.48094
## 2 2 1 disp 0.71834 0.70895 18.12961
## 3 3 1 hp 0.60244 0.58919 37.11264
## 4 4 1 qsec 0.17530 0.14781 107.06962
## 5 5 2 hp wt 0.82679 0.81484 2.36900
## 6 6 2 wt qsec 0.82642 0.81444 2.42949
## 7 7 2 disp wt 0.78093 0.76582 9.87910
## 8 8 2 disp hp 0.74824 0.73088 15.23312
## 9 9 2 disp qsec 0.72156 0.70236 19.60281
## 10 10 2 hp qsec 0.63688 0.61183 33.47215
## 11 11 3 hp wt qsec 0.83477 0.81706 3.06167
## 12 12 3 disp hp wt 0.82684 0.80828 4.36070
## 13 13 3 disp wt qsec 0.82642 0.80782 4.42934
## 14 14 3 disp hp qsec 0.75420 0.72786 16.25779
## 15 15 4 disp hp wt qsec 0.83514 0.81072 5.00000
逐步回归主要解决的是多变量共线性问题,也就是不是线性无关的关系,它是基于变量解释性来进行特征提取的一种回归方法。
逐步回归的主要做法有三种:
(一)Forward selection:将自变量逐个引入模型,引入一个自变量后要查看该变量的引入是否使得模型发生显著性变化(F检验),如果发生了显著性变化,那么则将该变量引入模型中,否则忽略该变量,直至所有变量都进行了考虑。即将变量按照贡献度从大到小排列,依次加入。
步骤:
(1)建立每个自变量与因变量的一元回归方程:
(2)分别计算m个一元回归方程中的回归系数的检验统计量F,并求出最大值为,
若,停止筛选,否则将
选入变量集,此时可以将
看做
,进入步骤(3)
(3)分别将自变量组与因变量建立二元回归方程,(此时
是步骤2中的
)计算方程中
的回归系数检验统计量F,取
,若
则停止筛选,否则将
选入变量集,此时将
看做
….如此迭代直到自变量的最大的F值小于临界值,此时回归方程就是最优的回归方程。
特点:自变量一旦选入,则永远保存在模型中;不能反映自变量选进模型后的模型本身的变化情况。
(2)Backward elimination:与Forward selection选择相反,在这个方法中,将所有变量放入模型,然后尝试将某一变量进行剔除,查看剔除后对整个模型是否有显著性变化(F检验),如果没有显著性变化则剔除,若有则保留,直到留下所有对模型有显著性变化的因素。即将自变量按贡献度从小到大,依次剔除。
步骤:
(1)建立全部对因变量y的回归方程,对方程中的m个自变量进行F检验,取最小值为:
,若
,在此时可另
为
,进入步骤(2)
(2)建立与因变量y的回归方程,对方程中的回归系数进行F检验,取最小值
,若
剔除,此时设
为
,…,一直迭代下去,直到各变量的回归系数F值均大于临界值,即方程中没有变量可以剔除为止,此时的回归方程就是最优的回归方程。
特点:自变量一旦剔除,则不再进入模型;开始把全部自变量引入模型,计算量过大。
(3)Bidirectional elimination:逐步筛选法。是在第一个的基础上做一定的改进,当引入一个变量后,首先查看这个变量是否使得模型发生显著性变化(F检验),若发生显著性变化,再对所有变量进行t检验,当原来引入变量由于后面加入的变量的引入而不再显著变化时,则剔除此变量,确保每次引入新的变量之前回归方程中只包含显著性变量,直到既没有显著的解释变量选入回归方程,也没有不显著的解释变量从回归方程中剔除为止,最终得到一个最优的变量集合。
该plot方法显示了所有可能的回归方法的拟合 。
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
k <- ols_all_subset(model)
plot(k)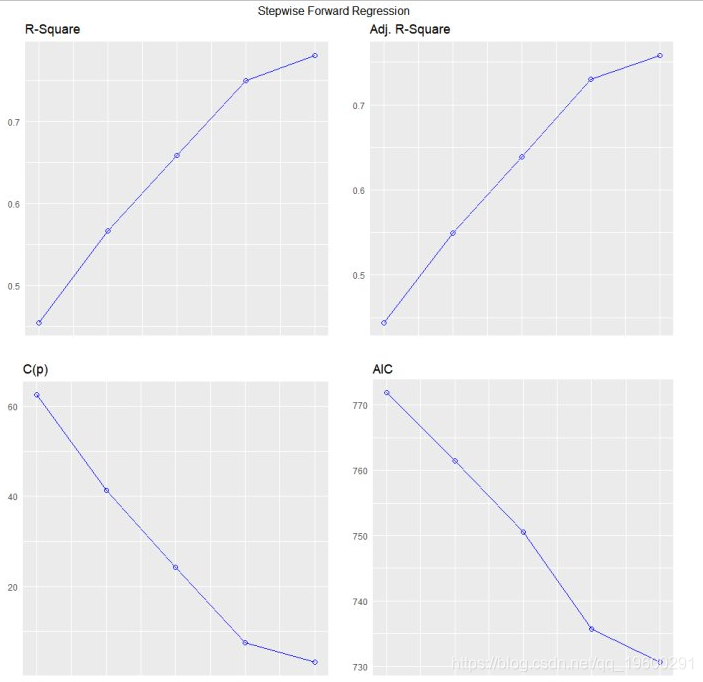
最佳子集回归
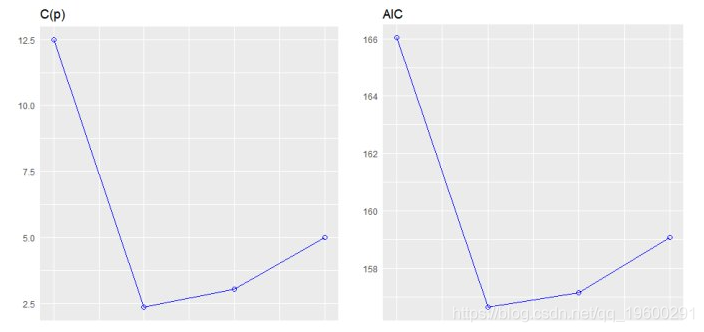
选择在满足一些明确的客观标准时做得最好的预测变量的子集,例如具有最大R2值或最小MSE, Cp或AIC。
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
ols_best_subset(model)
## Best Subsets Regression
## ------------------------------
## Model Index Predictors
## ------------------------------
## 1 wt
## 2 hp wt
## 3 hp wt qsec
## 4 disp hp wt qsec
## ------------------------------
##
## Subsets Regression Summary
## -------------------------------------------------------------------------------------------------------------------------------
## Adj. Pred
## Model R-Square R-Square R-Square C(p) AIC SBIC SBC MSEP FPE HSP APC
## -------------------------------------------------------------------------------------------------------------------------------
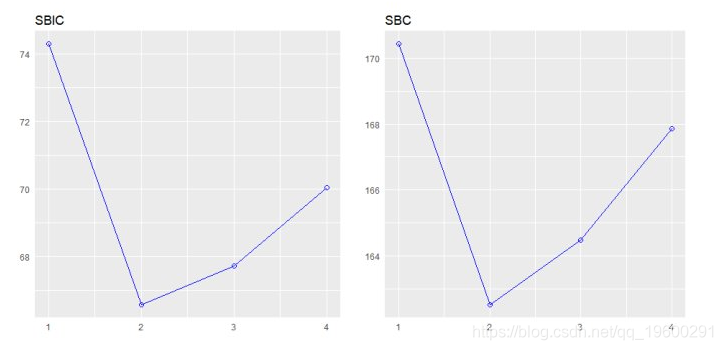
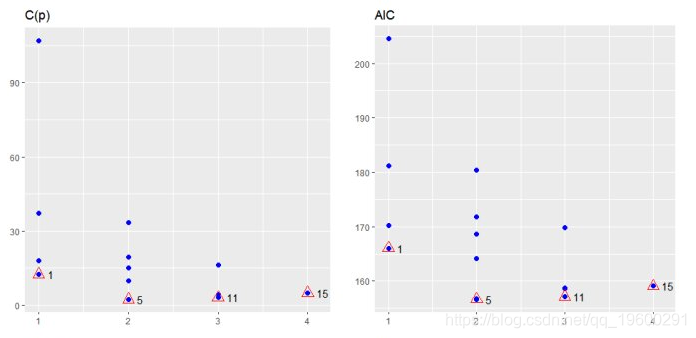
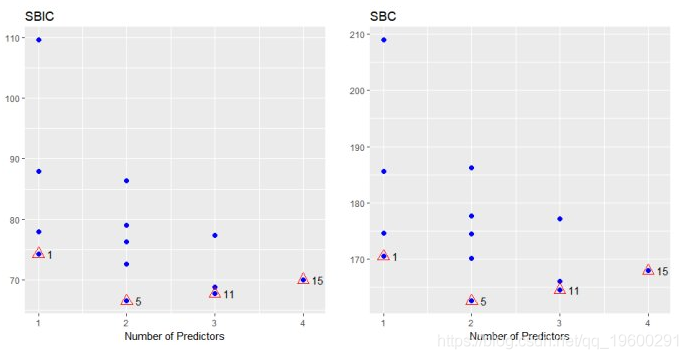
## 1 0.7528 0.7446 0.7087 12.4809 166.0294 74.2916 170.4266 9.8972 9.8572 0.3199 0.2801
## 2 0.8268 0.8148 0.7811 2.3690 156.6523 66.5755 162.5153 7.4314 7.3563 0.2402 0.2091
## 3 0.8348 0.8171 0.782 3.0617 157.1426 67.7238 164.4713 7.6140 7.4756 0.2461 0.2124
## 4 0.8351 0.8107 0.771 5.0000 159.0696 70.0408 167.8640 8.1810 7.9497 0.2644 0.2259
## -------------------------------------------------------------------------------------------------------------------------------
## AIC: Akaike Information Criteria
## SBIC: Sawa's Bayesian Information Criteria
## SBC: Schwarz Bayesian Criteria
## MSEP: Estimated error of prediction, assuming multivariate normality
## FPE: Final Prediction Error
## HSP: Hocking's Sp
## APC: Amemiya Prediction Criteriamodel <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
k <- ols_best_subset(model)
plot(k)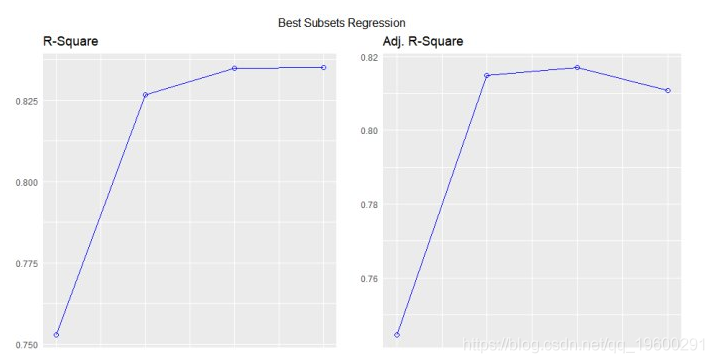

逐步前进回归
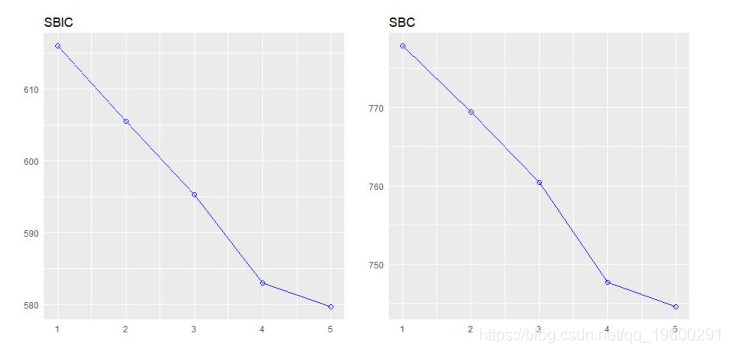
从一组候选预测变量中建立回归模型,方法是逐步输入基于p值的预测变量,直到没有变量进入变量。该模型应该包括所有的候选预测变量。如果细节设置为TRUE,则显示每个步骤。
变量选择
#向前逐步回归
model <- lm(y ~ ., data = surgical)
ols_step_forward(model)
## We are selecting variables based on p value...
## 1 variable(s) added....
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## No more variables satisfy the condition of penter: 0.3
## Forward Selection Method
##
## Candidate Terms:
##
## 1 . bcs
## 2 . pindex
## 3 . enzyme_test
## 4 . liver_test
## 5 . age
## 6 . gender
## 7 . alc_mod
## 8 . alc_heavy
##
## ------------------------------------------------------------------------------
## Selection Summary
## ------------------------------------------------------------------------------
## Variable Adj.
## Step Entered R-Square R-Square C(p) AIC RMSE
## ------------------------------------------------------------------------------
## 1 liver_test 0.4545 0.4440 62.5119 771.8753 296.2992
## 2 alc_heavy 0.5667 0.5498 41.3681 761.4394 266.6484
## 3 enzyme_test 0.6590 0.6385 24.3379 750.5089 238.9145
## 4 pindex 0.7501 0.7297 7.5373 735.7146 206.5835
## 5 bcs 0.7809 0.7581 3.1925 730.6204 195.4544
## ------------------------------------------------------------------------------
model <- lm(y ~ ., data = surgical)
k <- ols_step_forward(model)
## We are selecting variables based on p value...
## 1 variable(s) added....
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## No more variables satisfy the condition of penter: 0.3
plot(k)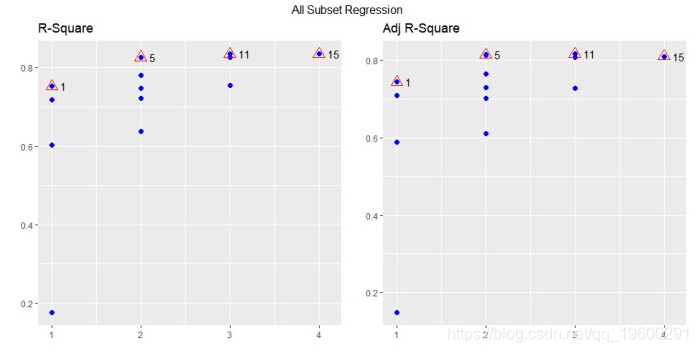
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析




2 comments on “R语言特征选择——逐步回归”