在保险定价中，风险敞口通常用作模型索赔频率的补偿变量。
如果我们必须使用相同的程序，但是一个程序的暴露时间为6个月，而另一个则是一年，那么自然应该假设平均而言，第二个驾驶员的事故要多两倍。
可下载资源
这是使用标准（均匀）泊松过程来建模索赔频率的动机。人们在这里还可以看到法律问题，因为如果（部分）退还保费，则可以按比例进行。风险与暴露成正比。因此，如果 Yi表示被保险人的理赔数量i，则具有特征Xi和风险敞口Ei，通过泊松回归，我们写
或等同
根据该表达式，曝光量的对数是一个解释变量，不应有系数（此处的系数取为1）。我们不能使用暴露作为解释变量吗？我们会得到一个单位参数吗？
当然，在进行费率评估的过程中，这可能不是一个相关的问题，因为精算师需要预测年度索赔频率（因为保险合同应提供一年的保险期）。但是，更好地了解人们为什么会离开我们的投资组合（例如，在任期前取消保险单，或者某天不续签）可能会很有趣。
为了更具体和更好地理解，请考虑以下模型：考虑使用Poisson流程对索赔到达进行建模，以及专职于其保险公司的人员。
> n=983
> D1=as.Date("01/01/1993",'%d/%m/%Y')
> D2=as.Date("31/12/2013",'%d/%m/%Y')
> for(i in 1:n){
+ expo=D2-arrival[i]
+ w=0
+ while(max(w)<expo) w=c(w,max(w)+1+trunc(rexp(1,1/1000)))
+ exposure[i]=departure[i]-arrival[i]
+ N[i]=max(0,length(w)-2)}
> df=data.frame(N=N,E=exposure/365)在这里，两次索赔之间的预期时间为1000天。泊松过程的（年度）强度在这里
> 365/1000
[1] 0.365因此，如果我们对曝光的对数进行Poisson回归，我们应该获取一个相近参数
> log(365/1000)
[1] -1.007858在这里，具有偏移量的常数的回归为
> summary(reg)
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-3.4145 -0.4673 0.2367 0.8770 3.6828
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.04233 0.02532 -41.17 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1116.9 on 982 degrees of freedom
Residual deviance: 1116.9 on 982 degrees of freedom
AIC: 3282.9
Number of Fisher Scoring iterations: 5这与我们刚才所说的一致。如果我们以曝光量的对数作为可能的解释变量进行回归，则我们期望其系数接近1。
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-3.0810 -0.8373 -0.1493 0.5676 3.9001
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.03350 0.08546 -12.09 <2e-16 ***
log(E) 1.00920 0.03292 30.66 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2553.6 on 982 degrees of freedom
Residual deviance: 1064.2 on 981 degrees of freedom
AIC: 3762.7
Number of Fisher Scoring iterations: 5如果我们保留偏移量并添加变量，我们可以看到它变得无用（对单位参数的测试）
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-3.0810 -0.8373 -0.1493 0.5676 3.9001
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.033503 0.085460 -12.093 <2e-16 ***
log(E) 0.009201 0.032920 0.279 0.78
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1064.3 on 982 degrees of freedom
Residual deviance: 1064.2 on 981 degrees of freedom
AIC: 3762.7
Number of Fisher Scoring iterations: 5在这里，我们确实具有纯泊松过程，因此曝光至关重要，因为泊松分布的参数与曝光成正比。但是我们不能从曝光中学到其他东西。
考虑一些真实数据。
nocontrat exposition zone puissance agevehicule
1 27 0.87 C 7 0
2 115 0.72 D 5 0
3 121 0.05 C 6 0
4 142 0.90 C 10 10
5 155 0.12 C 7 0
6 186 0.83 C 5 0
ageconducteur bonus marque carburant densite region nbre
1 56 50 12 D 93 13 0
2 45 50 12 E 54 13 0
3 37 55 12 D 11 13 0
4 42 50 12 D 93 13 0
5 59 50 12 E 73 13 0
6 75 50 12 E 42 13 0如果考虑暴露的对数的泊松回归，将会得到什么？
> summary(reg)
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-0.3988 -0.3388 -0.2786 -0.1981 12.9036
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.83045 0.02822 -100.31 <2e-16 ***
log(exposition) 0.53950 0.02905 18.57 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 12931 on 49999 degrees of freedom
Residual deviance: 12475 on 49998 degrees of freedom
AIC: 16150
Number of Fisher Scoring iterations: 6如果将曝光量添加到偏移量中，会发生什么情况？（我们使用非参数转换，可视化发生的情况）
plot(reg,se=TRUE)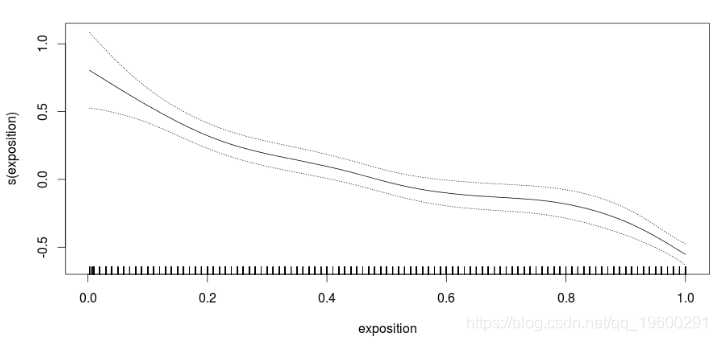
有明显而显着的效果。时间越长，他们获得索赔的可能性就越小。实际上，无需进行回归即可观察到它。
> plot(h1$mids,h1$density,type='s',lwd=2,col="red")
> lines(h0$mids,h0$density,type='s',col='blue',lwd=2)
蓝色为没有索赔人的风险密度，红色为有一个或多个索赔人的风险密度。
因此，在这里，我们不能假设参数的单位值。这意味着什么 ？我们可以重现这种行为吗？
为了更好地理解被保险人，请考虑两种可能的行为。第一个是：如果公司在没有索赔的几年后没有提供大幅折扣，则被保险人可能会离开公司。例如，如果被保险人在5年内没有索偿，那么5年后，他将离开公司（例如，获得更高的价格）。该代码
> df=data.frame(N=N,E=exposure/365)如果我考虑的是1500天而不是5年。
> summary(reg)
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5684 -0.9668 -0.2321 0.4244 3.6265
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.50844 0.10286 -24.39 <2e-16 ***
log(E) 1.65738 0.04494 36.88 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2567.31 on 982 degrees of freedom
Residual deviance: 885.71 on 981 degrees of freedom
此处，系数（明显）大于1。
> summary(reg)
Call:
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5684 -0.9668 -0.2321 0.4244 3.6265
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.50844 0.10286 -24.39 <2e-16 ***
log(E) 0.65738 0.04494 14.63 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1114.24 on 982 degrees of freedom
Residual deviance: 885.71 on 981 degrees of freedom
AIC: 2897.9这里显然存在偏见：长时间待在办公室的人更可能发生事故。这与我们的想法一致，因为客户的风险较低。
第二种行为是：有时，被保险人对索赔的处理方式不满意，他们可能会在第一次索赔后离开。考虑一种情况，在一项索赔之后，被保险人很可能（例如，概率为50％）离开公司。与其假设被保险人不喜欢理赔管理，不如考虑汽车被严重损坏以至于他不能再开车了。因此，支付保险费将毫无用处。这里的代码
> for(i in 1:n){
+ expo=D2-arrival[i]
+ w=0
+ exposure[i]=departure[i]-arrival[i]}
> df=data.frame(N=N,E=exposure/365)在这里，在每次索赔之后，被保险人扔硬币查看他是否取消合同。
Deviance Residuals:
Min 1Q Median 3Q Max
-2.28402 -0.47763 -0.08215 0.33819 2.37628
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.09920 0.04251 2.334 0.0196 *
log(E) 0.30640 0.02511 12.203 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 666.92 on 982 degrees of freedom
Residual deviance: 498.29 on 981 degrees of freedom
AIC: 2666.3这次，参数（再次显着）小于1。
Deviance Residuals:
Min 1Q Median 3Q Max
-2.28402 -0.47763 -0.08215 0.33819 2.37628
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.09920 0.04251 2.334 0.0196 *
log(E) -0.69360 0.02511 -27.625 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1116.87 on 982 degrees of freedom
Residual deviance: 498.29 on 981 degrees of freedom
AIC: 2666.3现在的情况已经大不相同了，因为那些待久的人应该不会遇到很多离开的机会。显然，他们没有太多要求。如果某人的风险敞口很大，那么上面输出中的负号表示该人平均应该没有太多债权。
如我们所见，这些模型产生了相当大的差异输出。注意，可能有更多的解释。例如，根据提取数据的方式，
- 在过去的二十年中，所有遵守的政策，
- 到现在为止所有在特定日期生效的政策
- 在某个特定日期生效的所有政策，直到之后的一年
- 现在生效的所有政策
到目前为止，我们一直在使用第一种方法，但是其他方法会产生不同的解释。
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言分类回归分析考研热现象分析与考研意愿价值变现
【专题】2024商业健康险与医药协同创新模式研究报告合集PDF分享（附原数据表）
