你们可能知道，实际极值分析有两种常用方法：分块极大值Blockmaxima、阈值超额法threshold excess。
今天，我们将分别介绍这两种方法。
分块极大值Block-maxima
分块样本极大值的极值理论(_Block_-_maxima_)。这种对（时间）观测序列的极值建模的方法是基于在一定的恒定长度序列内利用这些观测值的最大值或最小值。对于足够多 的_n个已建立块，这__n_个等长块 的所得峰值 可用于将合适的分布拟合到这些数据。虽然块大小基本上可以自由选择，但必须在偏差（小块）和方差（大块）之间进行权衡。通常，序列的长度通常选择对应于某个熟悉的时间段，在大多数情况下为一年。
EVT：Extreme Value Theory；预测小概率时间发生的可能，如大洪水，评估海事安全等。
EVT 中心思想是概率分布，可给出事件发生概率的数学公式。
例如常用的高斯分布，通常绝大多数数据不会偏离均值很多，但是对分布两端的极端值很难预测；属于小概率事件，事件越极端发生概率越低；此时计算发生概率可使用以往此类极端事件发生情况拟合曲线。
使用EVT流式检测异常值：Anomaly Detectionin Streams with Extreme Value Theory
检测流中的极端值问题可表述为，Xt是一段时间内的观测值，设置阈值zq，对任何>=0的时间 t，可观测到Xt > zq 的概率小于q(q很小)
之前常用的方法需要假设：正常数据发生有很高概率而异常发生概率很低，需要假设数据分布；而极值理论不需要假设样本数据的分布，通过理论结果推测低概率区域并找出异常点，这种单参数的方法适用于稳定样本和移动的样本。
在数学上，X是随机变量，F代表积累分布函数；F(X)=P(X<=x)；函数F的尾部分布为F(X)=1-F(X)=P(X>x)；用Xi代表随机变量和结果，通过上下文可明确它们的意思。对一个随机变量X和给定的概率q，记zq为它在1-q层的分位数，zq是最小值，P(X<=zq)>=1-q，P(X>zq)<q。
年度最大值（或最小值）的结果向量称为“年度最大值（最小值）系列”或简称为 AMS。
根据 Fisher-Tippett-Gnedenko 定理，块最大值的分布可以通过广义极值分布来近似。
以下代码显示了一个简短的实际示例，该示例使用 R 将广义极值分布拟合到降水数据的时间序列。样本数据集包含 1971 年至 2014 年 降水数据。
# 加载所需的包
# 获取数据
prexts <- rehyd
# 导出 AMS 以获得最大降水量
ams <- apprly
# GEV 分布的最大似然拟合
evd
# 诊断图
plotrl_mle <- reevel # 基于 L- 拟合 GEV 分布矩估计 # 诊断图 plot(fiom) # 重现水平： rm <- retvel # 重现水平图 plot loc <- as.numeric(retvel) # 带 LMOM 图的重现水平 loc <- as.numeric(return.level)
在这种情况下，两个结果非常相似。在大多数情况下，L 矩估计比最大似然估计更稳健。除了这些经典估计方法之外，还提供广义最大似然估计（GMLE， Martins 和 Stedinger，2000 年）和贝叶斯估计方法（Gilleland 和 Katz，2016 年）。
阈值超额法threshold excess
我们现在来看看阈值超额法。
根据 Coles (2001) 的说法，如果可以使用没有间隙的完整（时间）序列，则阈值方法比块最大值方法更有效，因为所有超过某个阈值的值都可以作为模型拟合的基础。在某些情况下，将分布拟合到块最大值数据是一种浪费的方法，因为每个块只有一个值用于建模，而阈值过剩方法可能会提供更多关于极端值的信息。
然而，类似于块最大值方法中块大小的选择，部分持续时间模型的阈值选择也受到偏差（低阈值）和方差（高阈值）之间的权衡。
Coles (2001) 描述了两种不同的阈值选择方法。首先，有一种基于平均_残差_寿命图的探索性方法。该技术在实际模型拟合之前应用。其次，另一种方法是评估参数估计的稳定性。因此，模型拟合的这种敏感性分析是在一系列不同的阈值范围内进行的。
随时关注您喜欢的主题
但是，选择合适的阈值可能是使用部分持续时间序列执行极值分析的最关键部分。Scarrott 和 MacDonald 在其 2012 年的文章A review of极值阈值估计和不确定性量化(REVSTAT 10(1): 33-59)中对阈值估计方法进行了很好的概述 。
找到合适的阈值后，超过该阈值的极值子集将用于拟合广义帕累托分布。
根据 Pickands-Balkema-de Haan 定理，超过阈值的值的分布可以近似为广义帕累托分布。
以下代码显示了一个简短的实际示例，该示例将广义帕累托分布拟合到降水数据的时间序列。样本数据集以 1981 年至 2014 年降水数据为特征。
# 平均剩余寿命图： lplot(prects) # 平均剩余寿命图描绘了阈值 (u) 与平均过剩流量。 # 这个想法是找到图几乎是线性的最低阈值； # 考虑到 95% 的置信范围。 # 在一系列阈值上拟合 GPD 模型 threplot(prxts) fitrange (prts) # 设置阈值 th <- 40 # 最大似然估计 pole <- fe # 诊断图 rl_mle <- retvel(po) # L-矩估计 d(as.vector(prmethod = "moments") # 诊断图 retel(pom) # 重现水平图 # 使用 MLE 的重现水平图 loc <- as.numeric # 带 LMOM 的重现水平图 plmom
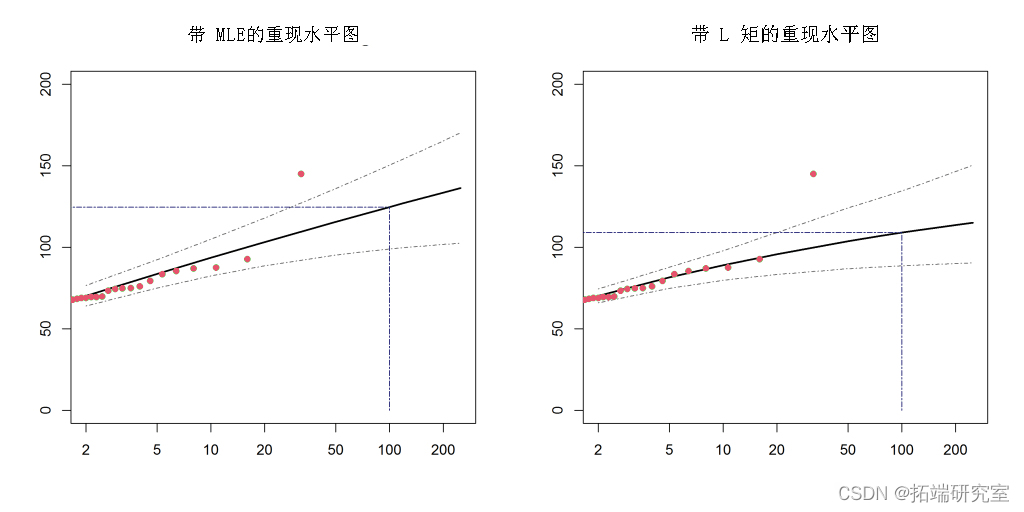
这个例子很好地说明了为什么基于 L 矩的方法可能优于最大似然估计，因为右图清楚地证明了使用 L 矩估计时异常值的影响要小得多。
除了这些经典估计方法之外，还有广义最大似然估计（GMLE， Martins 和 Stedinger，2000 年）和贝叶斯估计方法（Gilleland 和 Katz，2016 年）。
在最近关于分块最大值法和阈值超额法的文章中，我们简单地假设了极值分析的所有假设都得到了满足。然而，在处理环境变量时，情况很可能不是这样的。特别是平稳性的假设在很多情况下可能被违反。在全球气候变化的背景下，气象或其他环境变量的时间序列中很可能有一个相当大的趋势。当然，这种趋势必须被纳入分析中，因为由此产生的回归水平随时间而变化。
广义帕累托分布拟合
下面的代码显示了一个简短的实际例子，即使用R对降水数据的时间序列进行广义帕累托分布的拟合。样本数据集是从1971年到2013年的降水数据。
拟合线性模型的结果和图给人的印象都表明年最大降水量有上升趋势。
# 推导出最大降水的AMS值 as <- apprly(preax) # 检查AMS的平稳性。 # 简单的线性模型 summary(lm) p <- ggplot
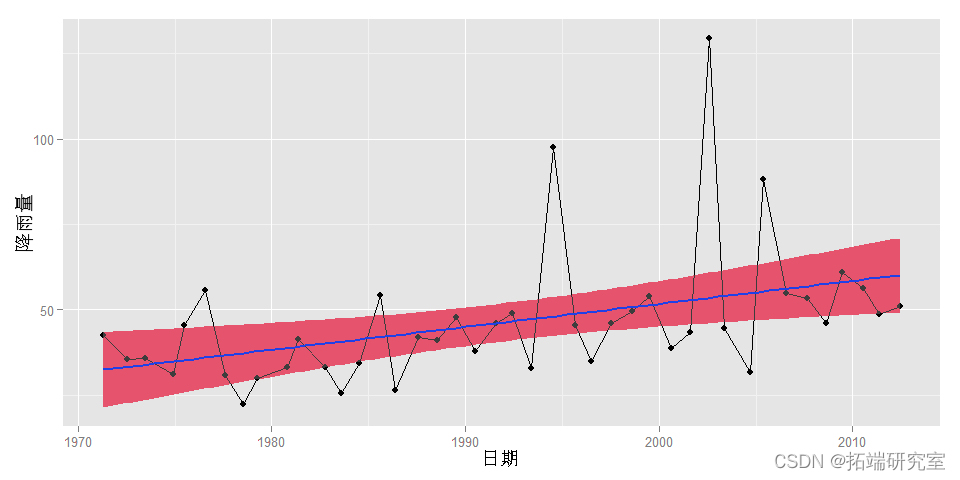
Mann-Kendall趋势检验的结果是一个非常小的P值，证实了这一趋势。因此，必须进行趋势校正，以说明随时间变化的回归水平。
# 最大似然估计 d( method = "MLE") # 重现水平图 plot(mend)
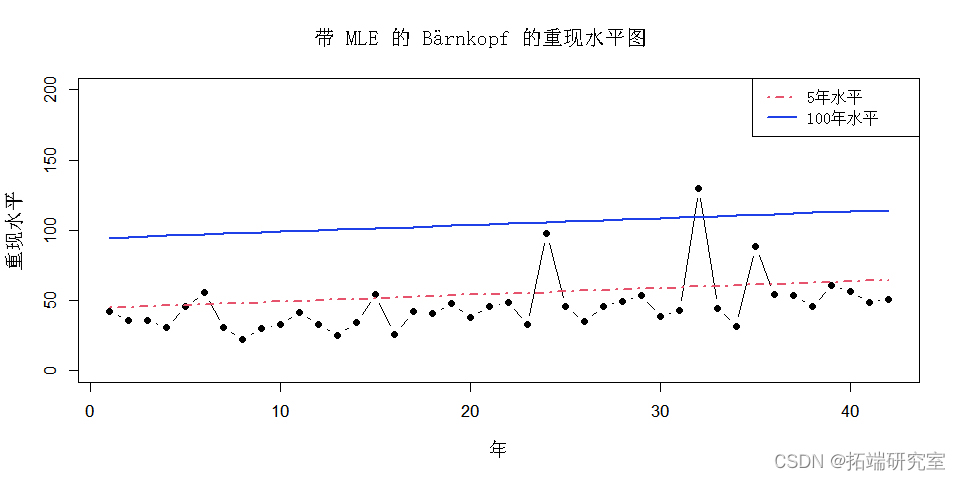
与前面的重现水平图（没有趋势）相比，这个重现水平图看起来有所不同。它显示的是5年和100年回归水平随时间的变化。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
