最近我们被客户要求撰写关于有限正态混合模型在r软件中的实现的研究报告，用于基于模型的聚类、分类和密度估计。
提供了通过EM算法对具有各种协方差结构的正态混合模型进行参数估计的函数，以及根据这些模型进行模拟的函数。
此外，还包括将基于模型的分层聚类、混合分布估计的EM和贝叶斯信息准则（BIC）结合在一起的功能，用于聚类、密度估计和判别分析的综合策略。其他功能可用于显示和可视化拟合模型以及聚类、分类和密度估计结果。
一个例子
高斯混合模型（Gaussian Mixed Model）指的是多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布但参数不一样，或者是不同类型的分布，比如正态分布和伯努利分布）。
如图1，图中的点在我们看来明显分成两个聚类。这两个聚类中的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM，那么只能用一个的二维高斯分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理，毕竟肉眼一看就觉得应该把它们分成两类。
图1
这时候就可以使用GMM了！如图2，数据在平面上的空间分布和图1一样，这时使用两个二维高斯分布来描述图2中的数据，分别记为 N ( μ 1 , Σ 1 ) \mathcal{N}(\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) N(μ1,Σ1)和 N ( μ 2 , Σ 2 ) \mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2) N(μ2,Σ2). 图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布 N ( μ 1 , Σ 1 ) \mathcal{N}(\boldsymbol{\mu_1}, \boldsymbol{\Sigma}_1) N(μ1,Σ1)和 N ( μ 2 , Σ 2 ) \mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2) N(μ2,Σ2)合成一个二维的分布，那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合，用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型（GMM）。
图2
聚类
head(X)
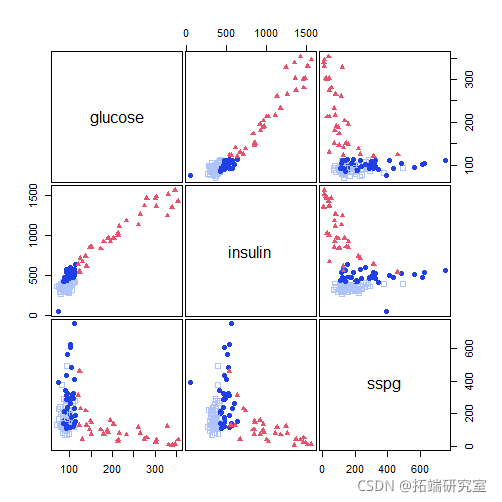
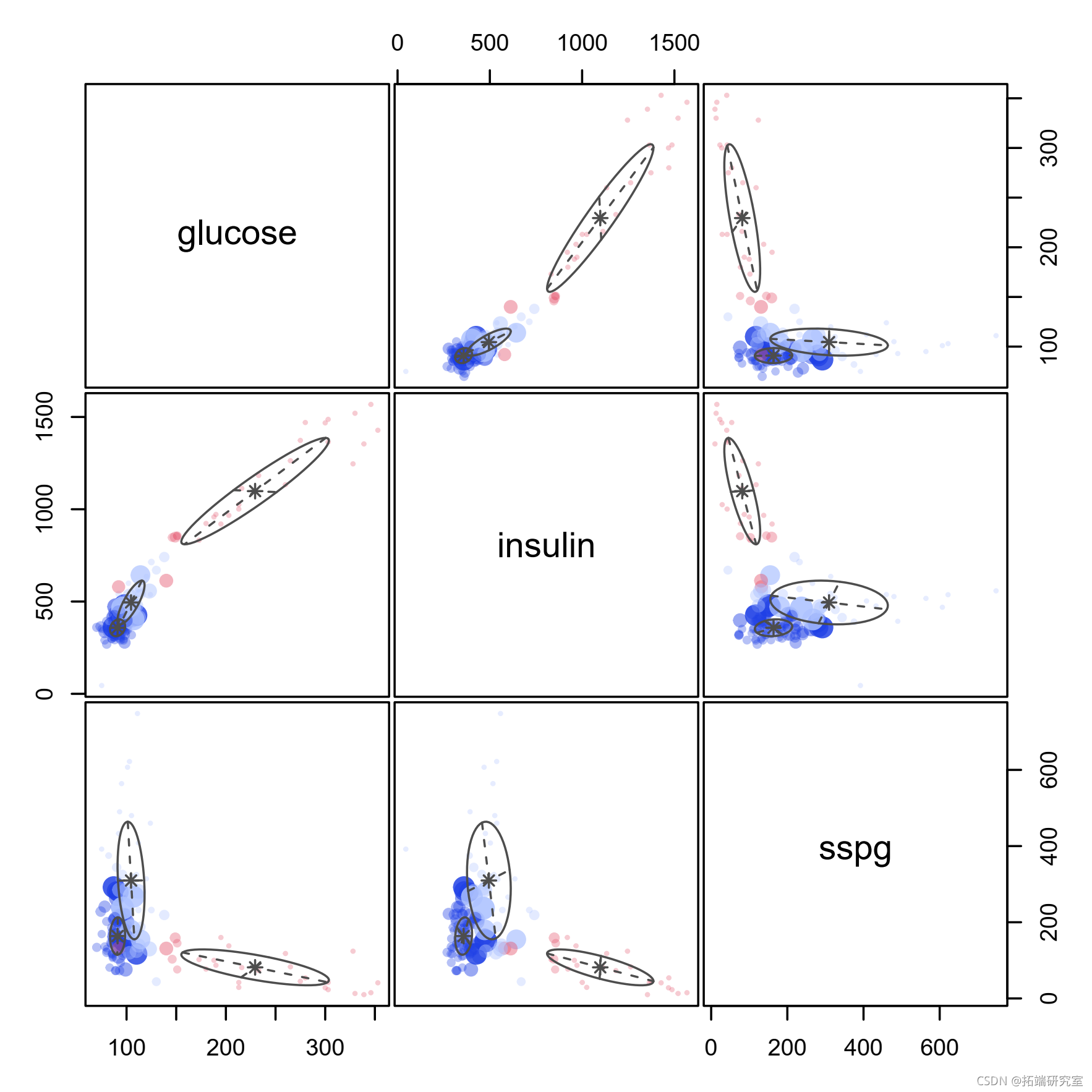
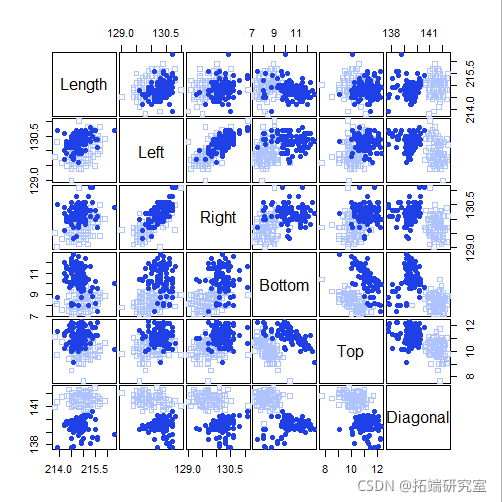
pairs(X)
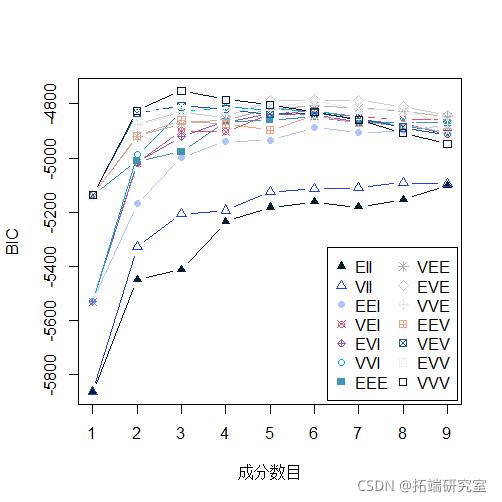
plot(BIC)
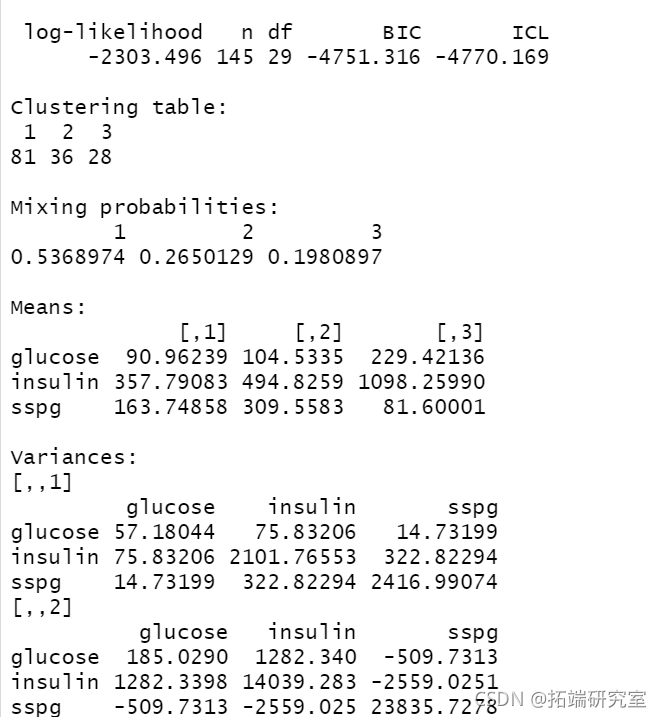
summary(BIC)
summary(mod1, parameters = TRUE)
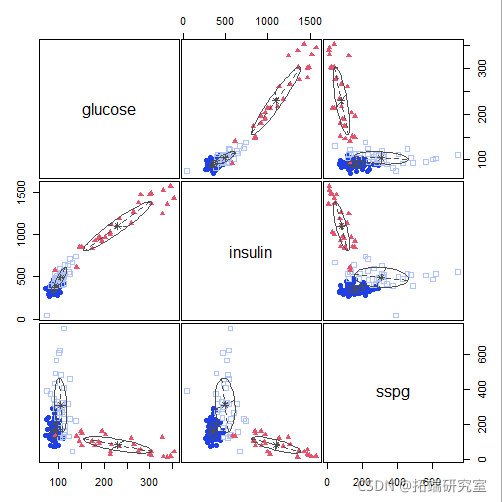
plot(mod1)
table(class, classification)
plot(mod1, what = "uncertainty")
随时关注您喜欢的主题
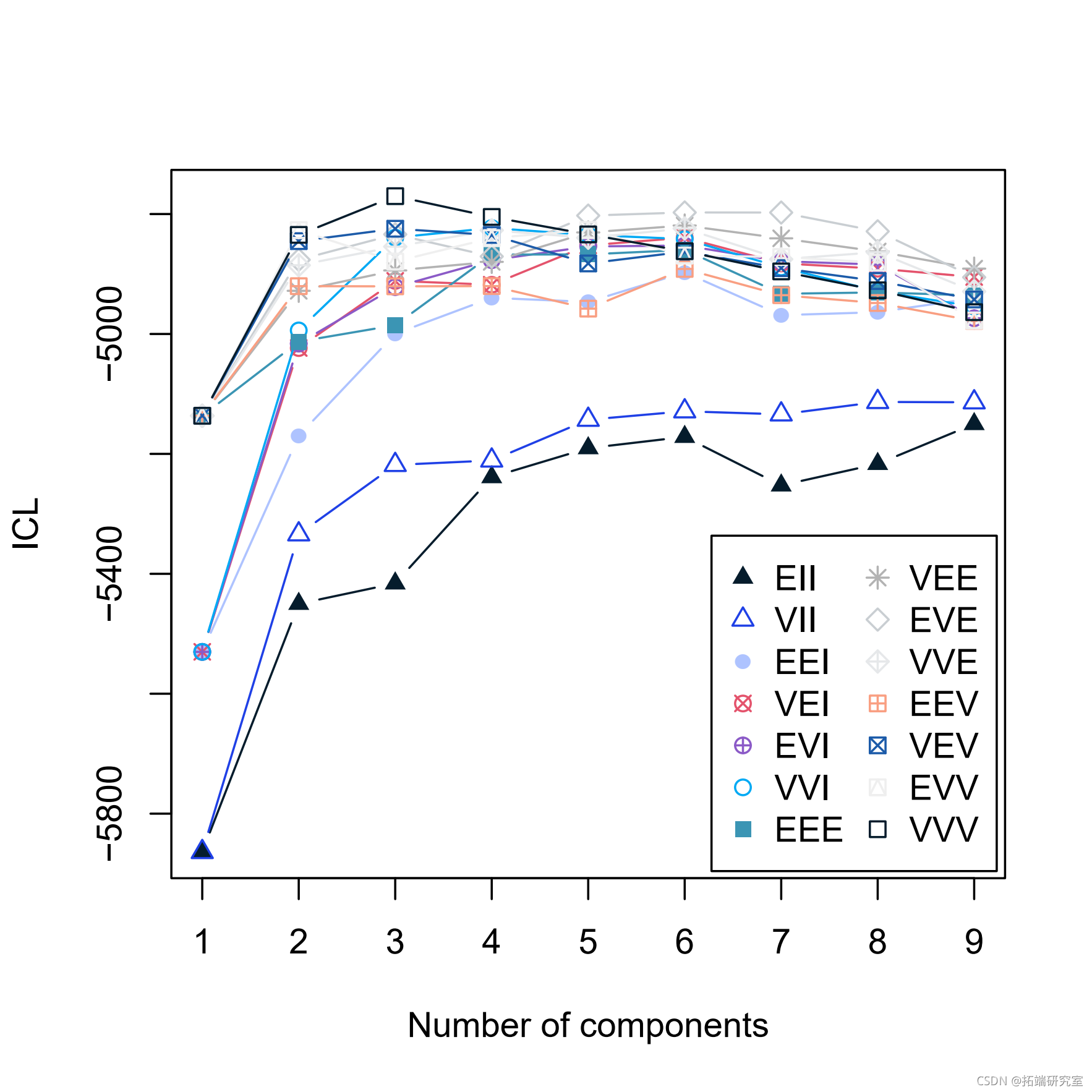
clustICL(X) summary(ICL)
BootstrapLRT(X)
初始化
使用EM算法进行最大似然估计。
EM的初始化是使用从聚类层次结构聚类中获得的分区来进行的。
hclust(X, use = "SVD"))
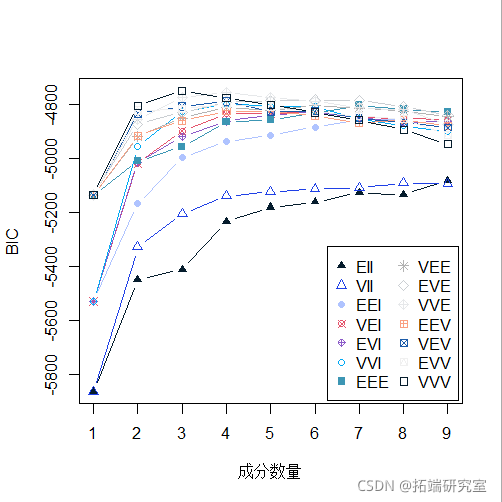
clustBIC(X, initialization )) # 默认
hc2
clustBIC(X, initialization )
hclust(X, model= "EEE"))
summary(BIC3)
通过合并最佳结果来更新BIC。
BIC(BIC1, BIC2, BIC3)
使用随机起点进行单变量拟合，通过创建随机集聚和合并最佳结果获得。
for(j in 1:20)
{
rBIC <- mclustBIC(
initi ))
BIC <- update(BIC, rBIC)
}
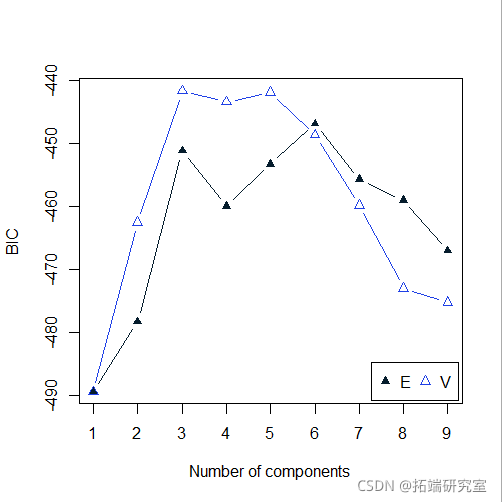
clust(ga, BIC)
分类
EDDA
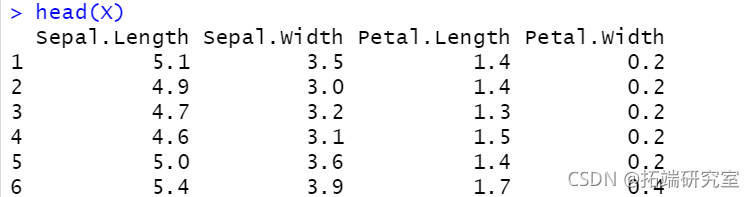
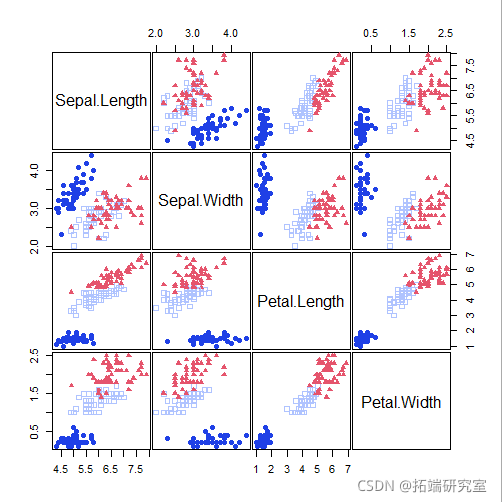
X <- iris\[,1:4\] head(X)
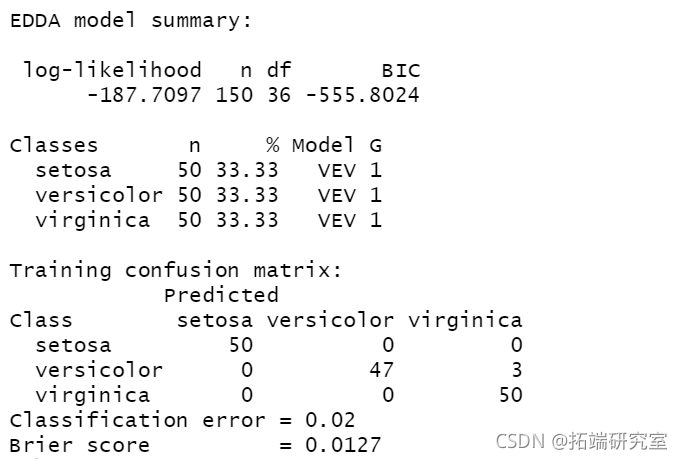
clustDA(X, class, "EDDA")
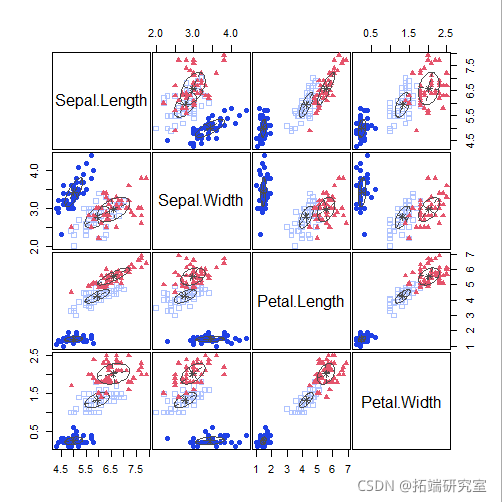
plot(mod2)
MclustDA
table(class)
head(X)
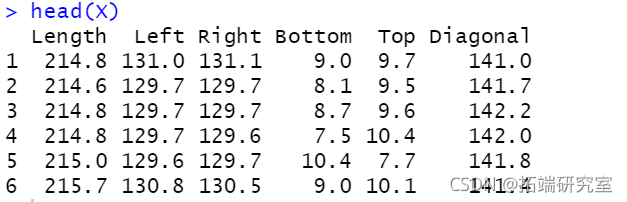
clustDA(X, class)
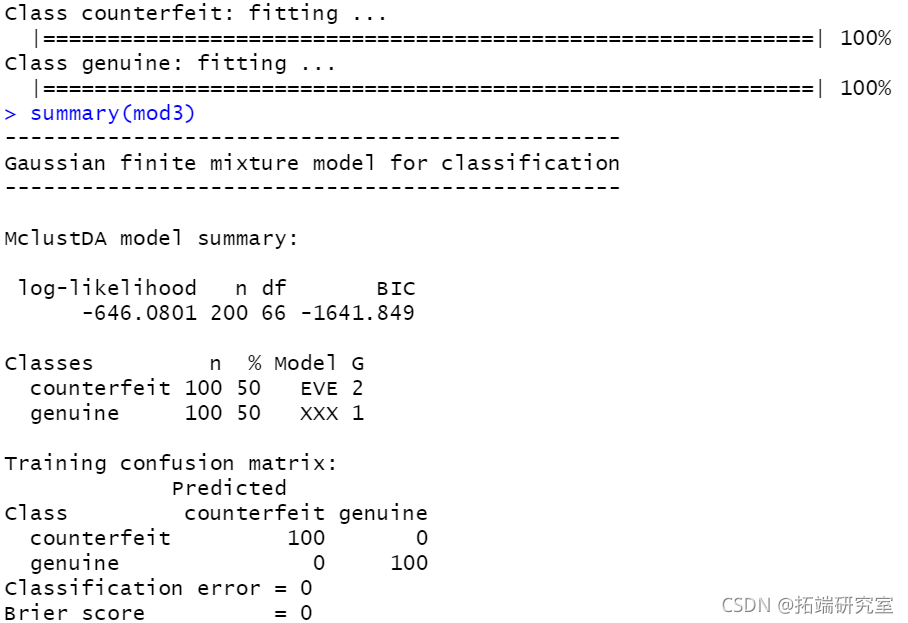
plot(mod3, 2)
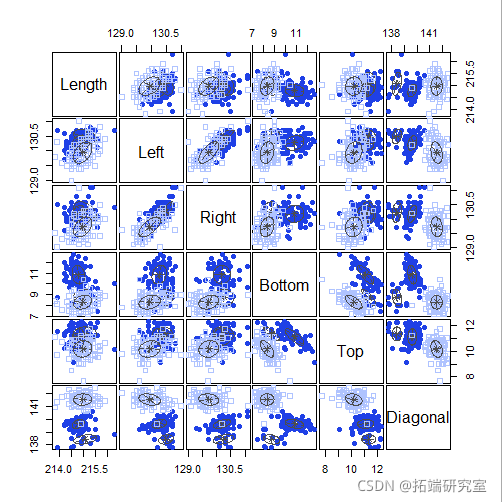
plot(mod3, 3)
交叉验证误差
cv(mod2, nfold = 10)
unlist(cv\[3:4\])
cv(mod3, nf = 10)
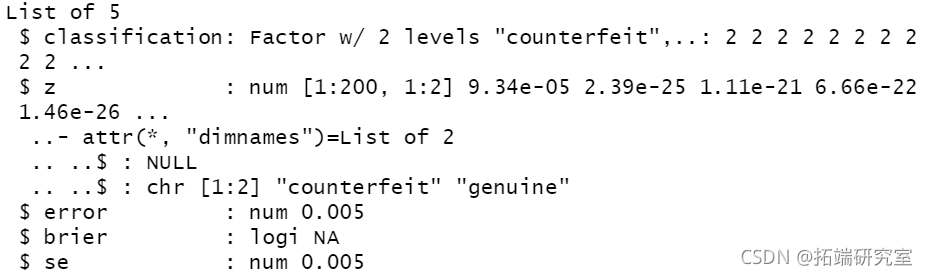
unlist(cv\[3:4\])
密度估计
单变量
clust(acid)
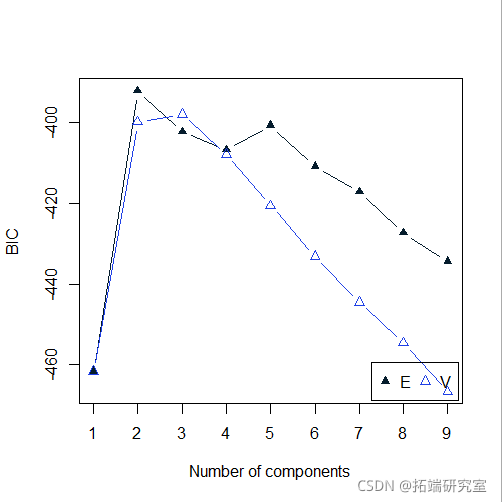
plot(mod4, "BIC")
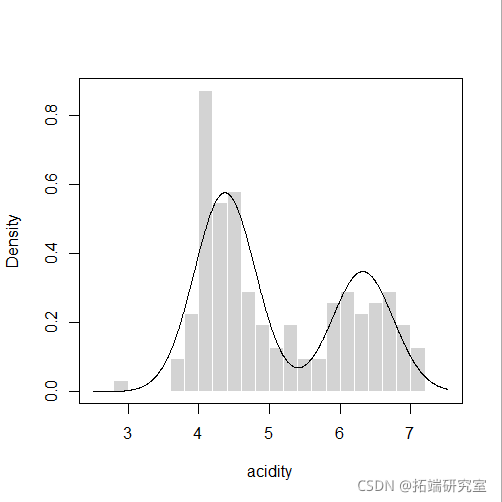
plot(mod4, "density", acidity)
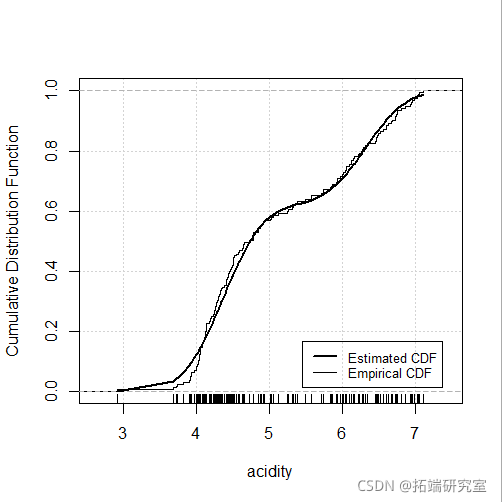
plot(mod4, "diagnostic", "cdf")
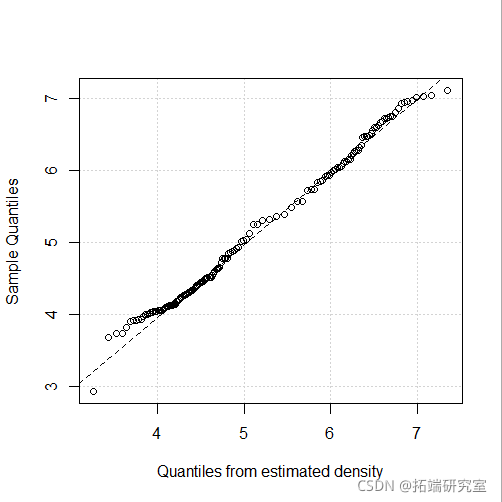
多变量
clu(faithful) summary(mod5)
plot(mod5, "BIC")
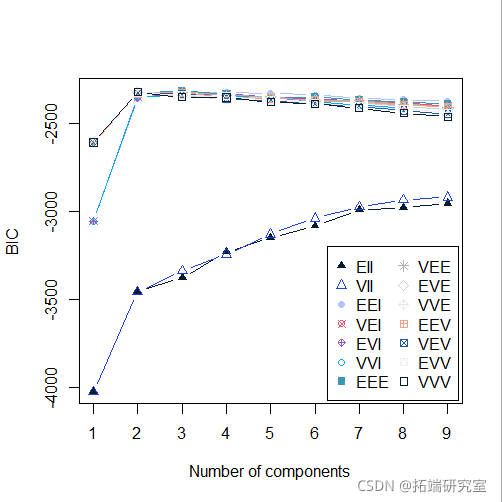
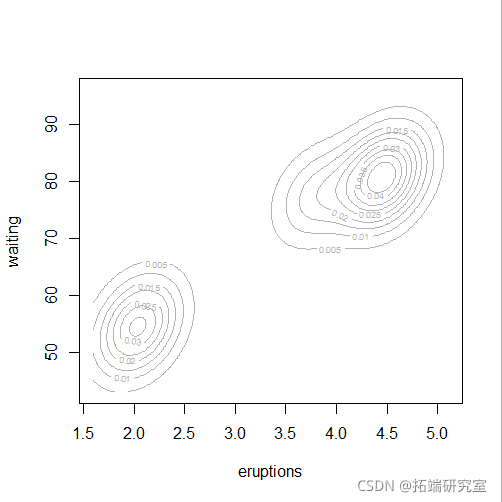
plot(mod5, "density",faithful)
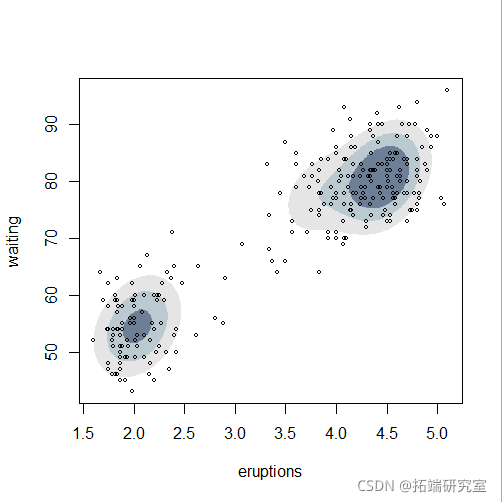
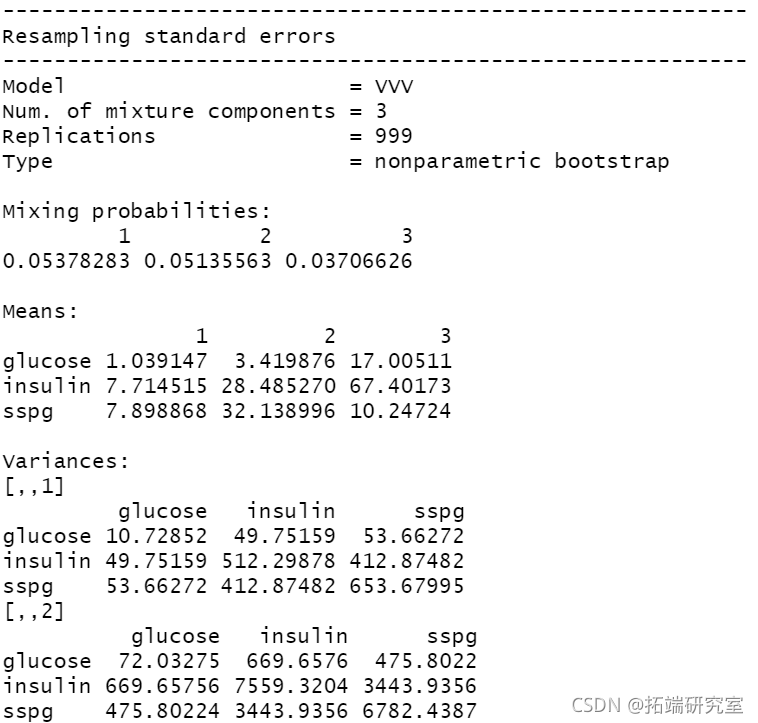
Bootstrap推理
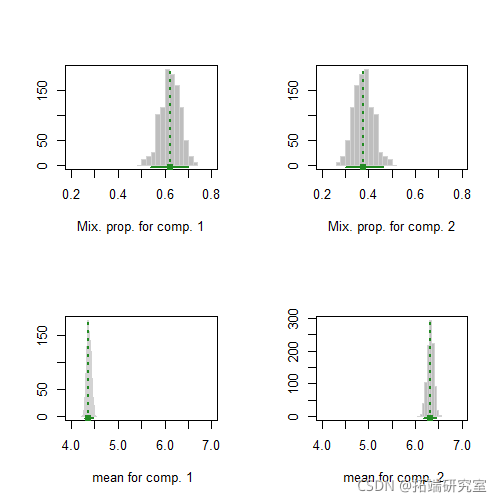
summary(boot1, what = "se")
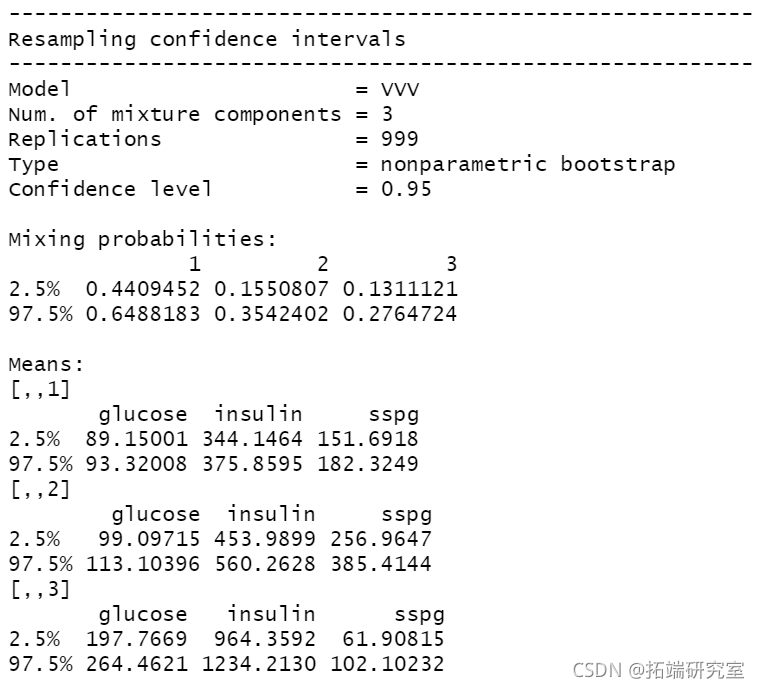
summary(boot1, what = "ci")
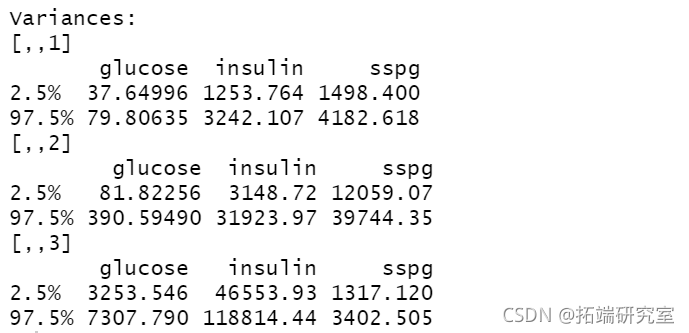
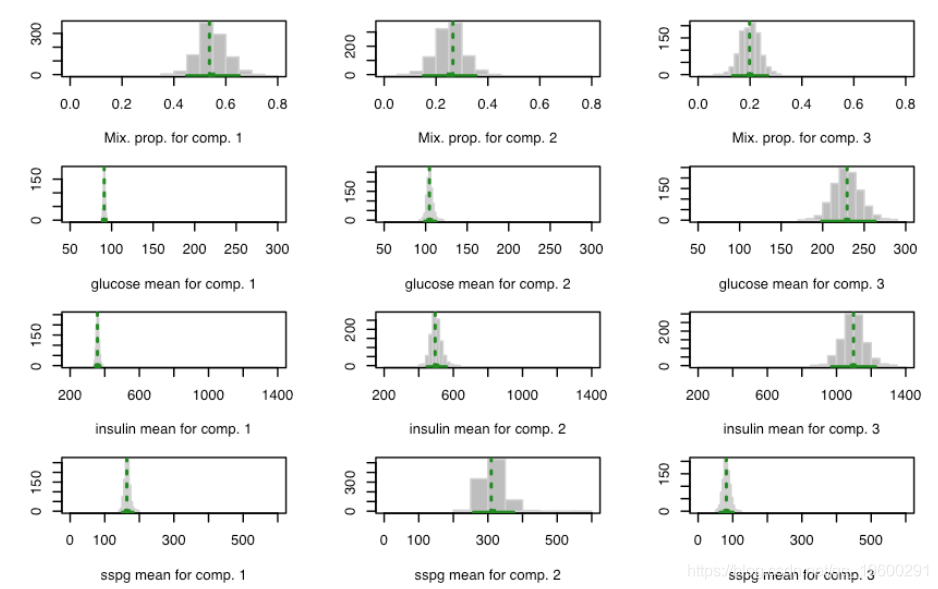
summary(boot4, what = "se") plot(boot4)
降维
聚类
plot(mod1dr, "pairs")
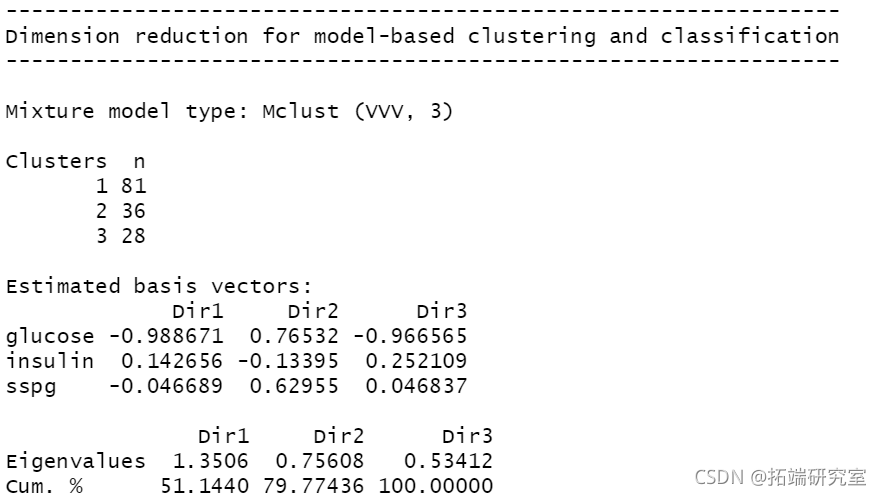
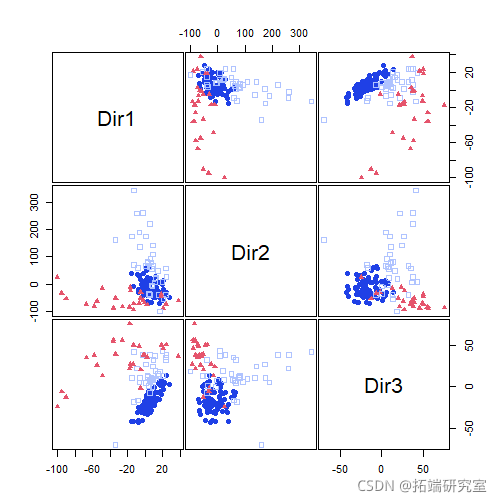
plot(mod1dr)
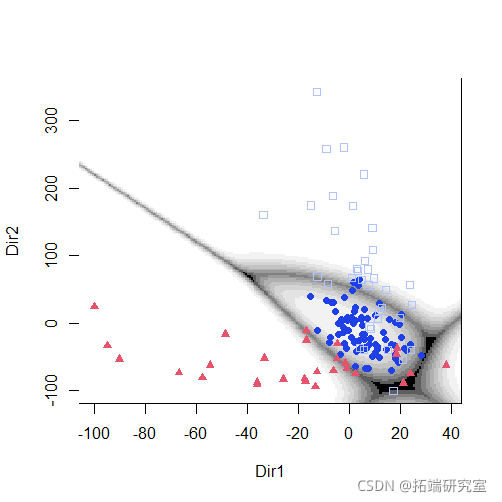
plot(mod1dr, "scatterplot")
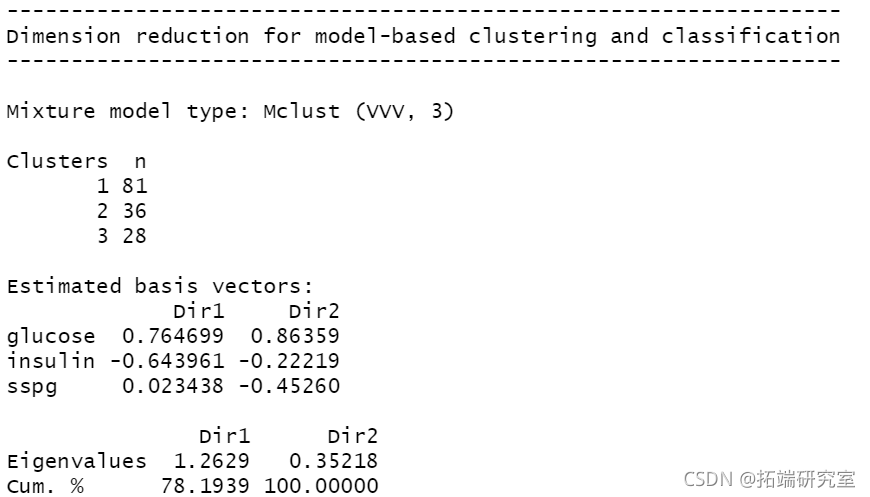
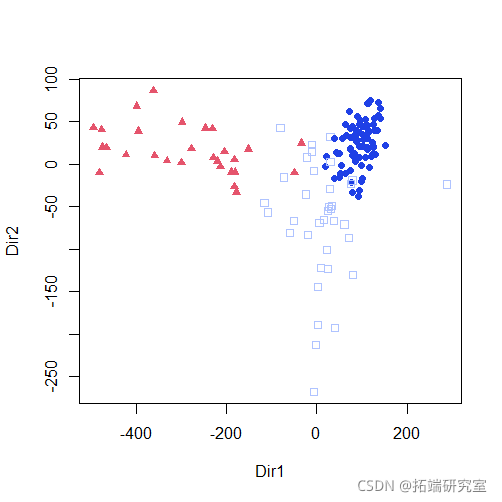
plot(mod1dr)
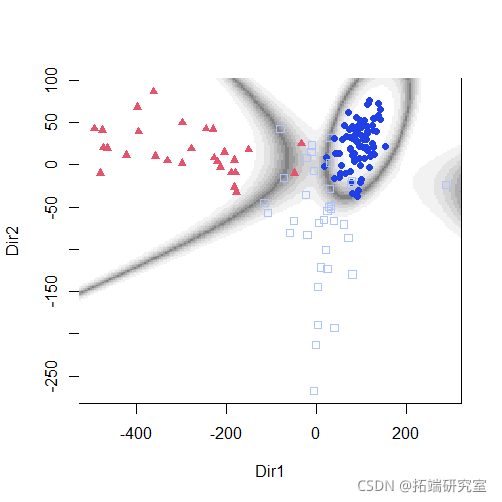
分类
summary(mod2dr) plot(mod2d)
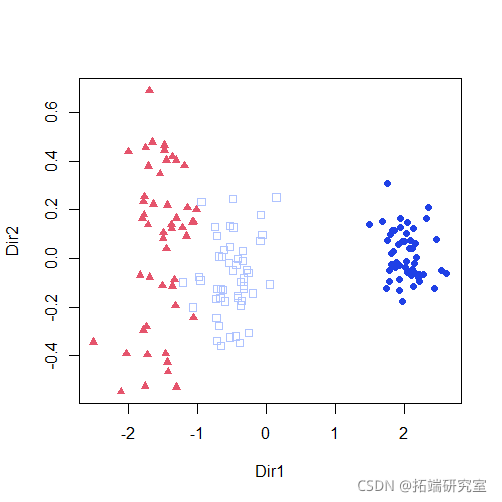
plot(mod2dr)
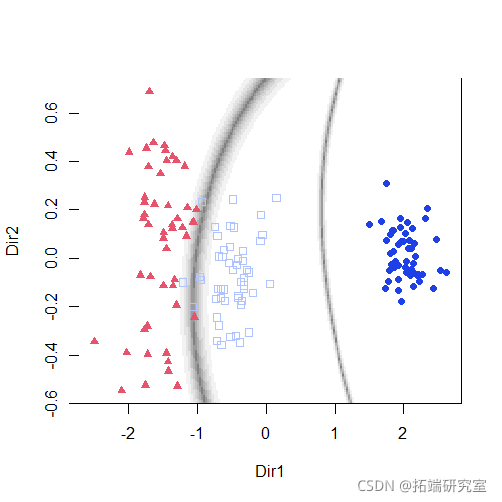
summary(mod3dr) plot(mod3dr)
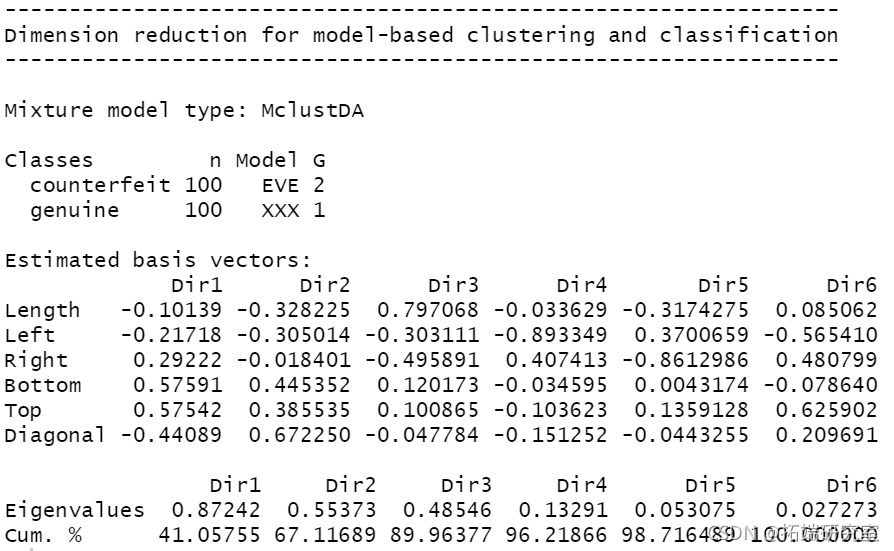
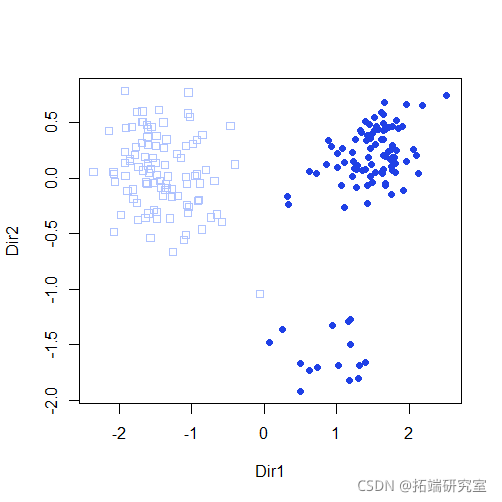
plot(mod3dr)
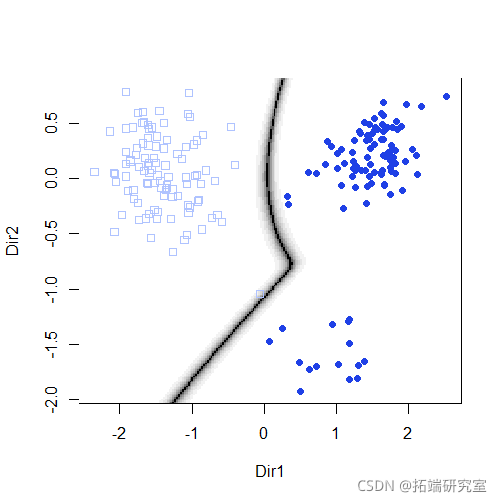
使用调色板
大多数图形都使用默认的颜色。
调色板可以定义并分配给上述选项，具体如下。
options("Colors" = Palette )
Pairs(iris\[,-5\], Species)
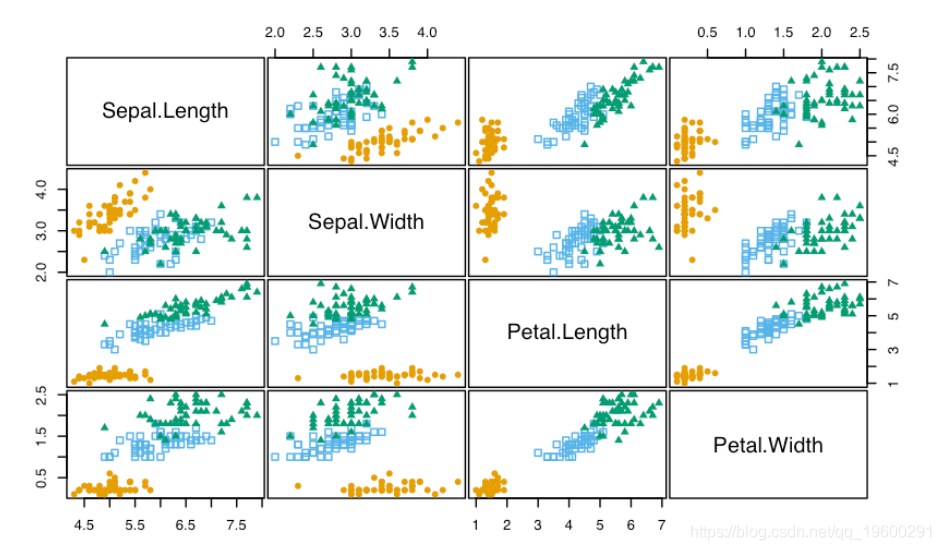
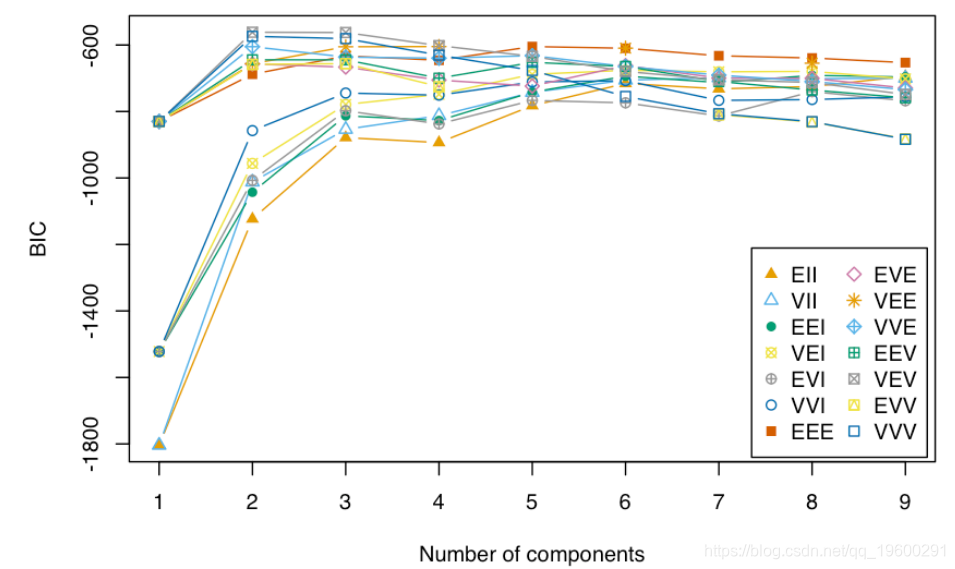
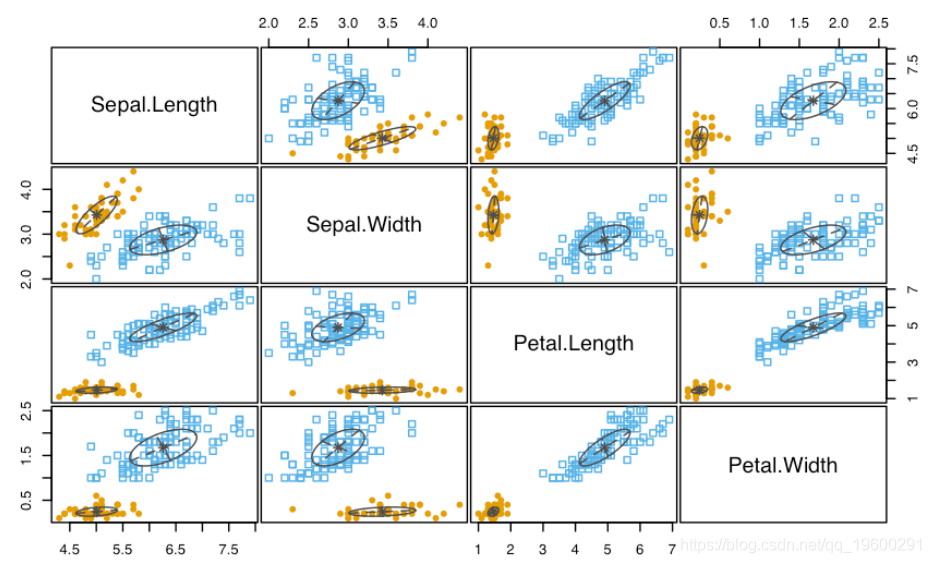
如果需要，用户可以很容易地定义自己的调色板。
参考文献
Fraley C. and Raftery A. E. (2002) Model-based clustering, discriminant analysis and density estimation, _Journal of the American Statistical Association_, 97/458, pp. 611-631.
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言层次聚类、多维缩放MDS分类RNA测序（RNA-seq）乳腺发育基因数据可视化|附数据代码
Python众筹项目结果预测：优化后的随机森林分类器可视化
SPSS大学生网络购物行为研究：因子分析、主成分、聚类、交叉表和卡方检验
R语言聚类分析、因子分析、主成分分析PCA农村农业相关经济指标数据可视化
