四种最常见的聚类方法模型是层次聚类，k均值聚类，基于模型的聚类和基于密度的聚类
可以基于两个主要目标评估良好的聚类算法：
- 高组内相似性
- 低组间相似性
可下载资源
混合模型（Mixture Model）
混合模型是一个可以用来表示在总体分布（distribution）中含有 K 个子分布的概率模型，换句话说，混合模型表示了观测数据在总体中的概率分布，它是一个由 K 个子分布组成的混合分布。混合模型不要求观测数据提供关于子分布的信息，来计算观测数据在总体分布中的概率。
高斯模型
单高斯模型
当样本数据 X 是一维数据（Univariate）时，高斯分布遵从下方概率密度函数（Probability Density Function）：
其中 为数据均值（期望），
为数据标准差（Standard deviation）。
当样本数据 X 是多维数据（Multivariate）时，高斯分布遵从下方概率密度函数：
其中， 为数据均值（期望），
为协方差（Covariance），D 为数据维度。
高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型，这 K 个子模型是混合模型的隐变量（Hidden variable）。一般来说，一个混合模型可以使用任何概率分布，这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。
举个不是特别稳妥的例子，比如我们现在有一组狗的样本数据，不同种类的狗，体型、颜色、长相各不相同，但都属于狗这个种类，此时单高斯模型可能不能很好的来描述这个分布，因为样本数据分布并不是一个单一的椭圆，所以用混合高斯分布可以更好的描述这个问题，如下图所示：
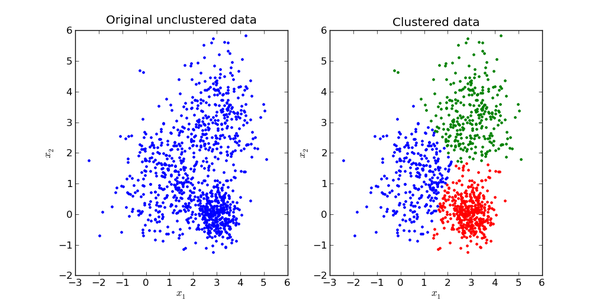
首先定义如下信息：
-
表示第
个观测数据，
-
是混合模型中子高斯模型的数量，
-
是观测数据属于第
个子模型的概率，
，
-
是第
。其展开形式与上面介绍的单高斯模型相同
-
表示第
高斯混合模型的概率分布为：
对于这个模型而言，参数 ，也就是每个子模型的期望、方差（或协方差）、在混合模型中发生的概率。
高斯混合模型
基于概率模型的聚类技术已被广泛使用，并且已经在许多应用中显示出有希望的结果，从图像分割，手写识别，文档聚类，主题建模到信息检索。基于模型的聚类方法尝试使用概率方法优化观察数据与某些数学模型之间的拟合。
生成模型通常使用EM方法求解，EM方法是用于估计有限混合概率密度的参数的最广泛使用的方法。基于模型的聚类框架提供了处理此方法中的几个问题的主要方法，例如密度（或聚类）的数量，参数的初始值（EM算法需要初始参数值才能开始），以及分量密度的分布（例如，高斯分布）。EM以随机或启发式初始化开始，然后迭代地使用两个步骤来解决计算中的循环：
- E-Step。使用当前模型参数确定将数据点分配给集群的预期概率。
- M-Step。通过使用分配概率作为权重来确定每个集群的最佳模型参数。
R中的建模
mb = Mclust(iris[,-5])
#或指定集群数
mb3 = Mclust(iris[,-5], 3)
# 或指定集群数
mb$modelName
# 或指定集群数
mb$G
# 在给定聚类中观察的概率
head(mb$z)
# 获取概率，均值，方差
summary(mb, parameters = TRUE)
table(iris$Species, mb$classification)
# 比较
table(iris$Species, mb3$classification)比较每个群集中的数据量
在将数据拟合到模型中之后，我们基于聚类结果绘制模型。
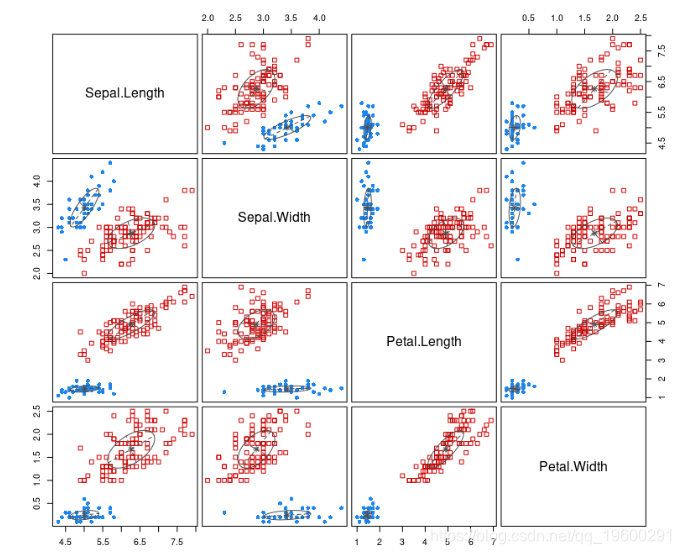
让我们绘制估计的密度。
plot(mb, "density")
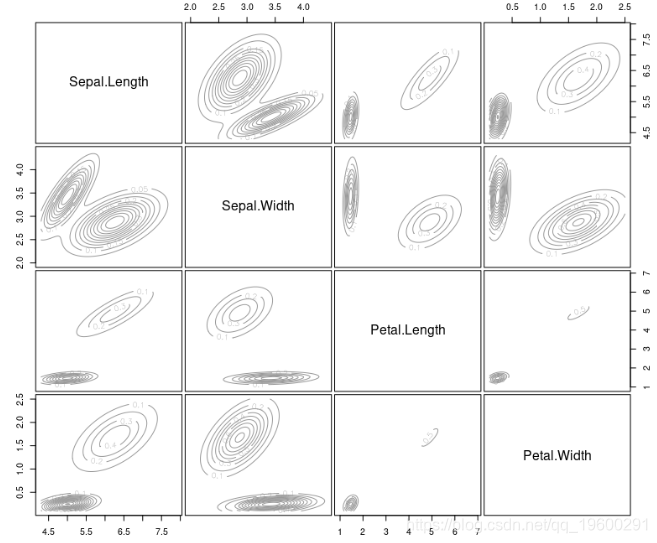
您还可以使用该summary()函数来获取最可能的模型和最可能数量的集群。对于此示例，最可能的簇数为5，BIC值等于-556.1142。
比较聚类方法
在使用不同的聚类方法将数据拟合到聚类中之后，您可能希望测量聚类的准确性。在大多数情况下，您可以使用集群内或集群间度量标准作为度量。集群间距离越高越好，集群内距离越低、越好。
接下来，检索聚类方法的集群验证统计信息：
通常，我们使用within.cluster.ss和avg.silwidth验证聚类方法。该within.cluster.ss测量表示所述簇内总和的平方，和avg.silwidth表示平均轮廓宽度。
within.cluster.ss测量显示了相关对象在群集中的紧密程度; 值越小，集群中的对象越紧密。avg.silwidth是一种度量，它考虑了群集中相关对象的紧密程度以及群集之间的区别程度。轮廓值通常为0到1; 接近1的值表明数据更好地聚类。
k-means和GMM之间的关系
K均值可以表示为高斯混合模型的特例。
通常，高斯混合有更好的表现力，因为数据的群集分配还取决于该群集的形状，而不仅仅取决于其接近度。
与k-means一样，用EM训练高斯混合模型可能对冷启动条件非常敏感。如果我们将GMM与k-means进行比较和对比，我们会发现前者的初始条件比后者更多。
结果
每个聚类被建模为多元高斯分布，并通过给出以下内容来指定模型：
- 集群数量。
- 每个群集中所有数据点的分数。
- 每个聚类的均值和它的协方差矩阵。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】Python深度神经网络DNNs-K-Means（K-均值）聚类方法在MNIST等数据可视化对比分析
Python量子计算聚类Q-means（量子k-means）算法分析电路数据实现可视化
TensorFlow深度学习框架改进K-means聚类、SOM自组织映射神经网络算法及上海招生政策影响分析研究
Python回归、聚类、相关分析上海公租房租金满意度影响因素数据可视化
