R语言曲线回归：多项式回归、多项式样条回归、非线性回归数据分析

本文将使用三种方法使模型适合曲线数据：1）多项式回归；2）用多项式样条进行B样条回归；3）进行非线性回归。

由Kaizong Ye，Coin Ge撰写

在此示例中，这三个中的每一个都将找到基本相同的最佳拟合曲线。

可下载资源

完整程序、数据和文档（word）

本文将使用三种方法使模型适合曲线数据：1）多项式回归；2）用多项式样条进行B样条回归；3）进行非线性回归。在此示例中，这三个中的每一个都将找到基本相同的最佳拟合曲线。

多项式回归

两个变数之间的关系不一定是简单的线性关系，可能是多种多样的曲线关系。

X在某一区间上，X和Y的关系有可能用线性描述，但X可能取值的区间而言，可能是非线性。

两个变数呈现曲线关系的回归称曲线回归（curvilinear regression）或非线性回归（non-linear regression）。

以最小二乘法分析曲线关系资料在数量变化上的特征和规律，称为曲线回归分析或非线性回归分析。

曲线角度看，线性回归仅是其中的一个特例：直线可看成是曲率为0的曲线。

一、曲线的类型与特点

根据曲线的性质和特点可大致分为6类：指数函数曲线，对数，幂函数，双曲，S型和多项式曲线。

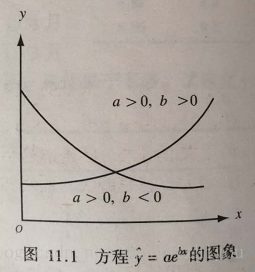
（1）指数函数曲线

指数函数（x 作为指数出现）方程形式： $\hat{y}=ae^{bx}$ 参数b一般用来描述增长或衰减的速度

$\hat{y}=ab^{x}$

$\hat{y}=ae^{bx}$ ,当 a>0、b>0时，y随x的增大而增大（增长），曲线凹向上；

当 a>0、b<0时，y随x的增大而减小（衰减），曲线也是凹向上。

（2）对数函数曲线

对数函数（x 作为自然对数出现）方程形式： $\hat{y}=a+bInx$ （x>0）

对数函数表示：x变数的较大变化可引起y变数的较小变化。

b>0时，y随x的增大而增大，曲线凸向上；

b<0时，y随x的增大而减小，曲线凹向上。

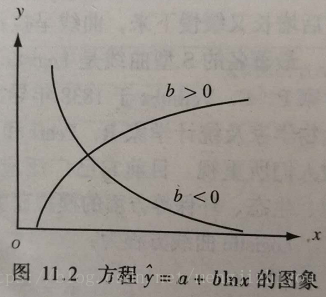
（3）幂函数曲线

对数函数（y是x某次幂的函数）方程形式： $\hat{y}=ax^{b}$

当 a>0、b>1时，y随x的增大而增大（增长），曲线凹向上；

当 a>0、0<b<1时，y随x的增大而增大（增长），但变化缓慢，曲线凸向上；

当 a>0、b<0时，y随x的增大而减小，曲线凹向上，且以x,y轴为渐近线。

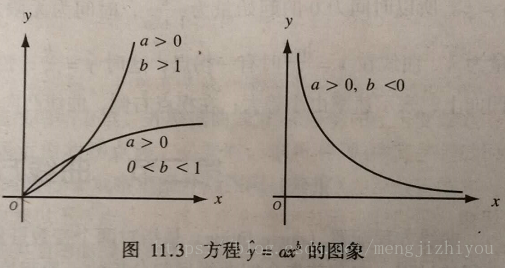
（4）双曲函数曲线：变形双曲线

方程形式：i: $\hat{y}=\frac{x}{a+bx}$

ii: $\hat{y}=\frac{a+bx}{x}$

iii: $\hat{y}=\frac{1}{a+bx}$

$\hat{y}=\frac{x}{a+bx}$ , 该曲线通过原点（0，0）

当 a>0、b>0时，y随x的增大而增大，但速率趋小，曲线凸向上，并向y=1/b渐进；

当 a>0、b<0时，y随x的增大而增大，速率趋大，曲线凹向上，并向x=-a/b渐进。

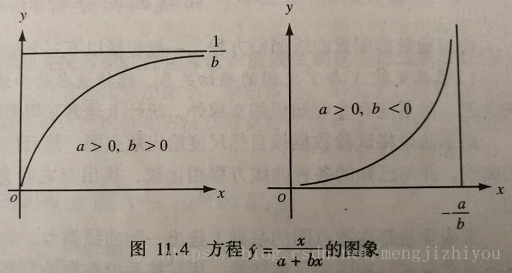
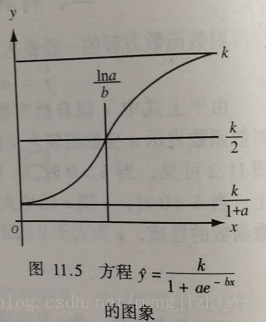
（5）S型曲线

主要描述动、植物的自然生长过程，又称生长曲线。

生长过程的基本特点是开始增长较慢，而在以后的某一范围内迅速增长，达到一定的限度后增长又缓慢下来，曲线呈拉长的‘S’型曲线。‘注明的S’型曲线是Logistic生长曲线。

Logistic曲线方程： $\hat{y}=\frac{k}{1+ae^{-bx}}$ (a、b、k均大于0)

x=0, $\hat{y}=\frac{k}{1+a}$ ; x $\rightarrow\infty$ , $\hat{y}=k$ ;

所以时间为0的起始量为 $\frac{k}{1+a}$ ，时间为无限延长的终极量为 k

曲线 $x=\frac{Ina}{b}$ 时有一个拐点，这时 $\hat{y}=\frac{k}{2}$ ，恰好是终极量k的一半

拐点左侧，曲线凹向上，速率由小趋大；拐点右侧，曲线凸向上，速率由大趋小。

二、曲线方程的配置

曲线方程配置（curve fitting）:指对两个变数资料进行曲线回归分析，获得一个显著的曲线方程的过程。

1、曲线回归分析的一般程序

由试验数据配置曲线回归方程，包括以下三个步骤：

（1）根据变数X和Y之间的确切关系，选择适当的曲线类型

确定曲线类型是曲线回归分析的关键。除了应有专业知识支撑外，统计上通常采用图示法和直线化法辅助选择。

图示法：将试验数据按自然尺度绘出散点图，然后按照散点趋势画出反映它们之间变化规律的曲线，并与已知的各种曲线方程相比较，找出与之最为相似的曲线图形，作为选定的曲线类型。

直线化法：是在散点图的基础上选出一种曲线类型，对该曲线方程进行尺度转换使之直线化，再将原数据进行相同的尺度转换，用转换后的数据绘出新的散点图。若此散点图具有直线趋势，即表明选取的曲线类型是恰当的。

（2）对选定的曲线类型，在线性化后按最小二乘法原理配置直线回归方程，并作显著性测验

求得两变数或转换后的新变数间的线性相关系数 $r_{yx}$ 。

若此 $r_{yx}$ 不显著，则分析结束，表明所选曲线方程不适合；

若 $r_{yx}$ 显著，则表明所选曲线方程在统计上是恰当的，可继续求解回归统计数，获得直线回归方程。

（3）将直线回归方程转换成相应的曲线方程，并对有关统计参数作出推断

获得显著的直线回归方程后，可直接反转换成相应的曲线回归方程，并根据曲线方程的特性估计有关参数，包括回归参数、极小值、极大值、渐进值和拐点等。必要时，可利用曲线方程进行x观察范围内的预测（内插），或在论据充足时进行x观察范围外的预测（外推）。

应用上述程序配置曲线方程，注意点如下：

（1）若同一资料用两种或两种以上不同类型的曲线方程配置，结果均为显著，则需选择其中最佳的曲线方程。判别的统计标准是不同曲线方程下离回归平方和 $\sum (y-\hat{y})^{2}$ 的大小， $\sum (y-\hat{y})^{2}$ 最小者当选。也可直接根据直线化后的 $r_{yx}$ 的绝对值大小直接确定。

（2）若进行转换后仍无法找出显著的直线化方程，可考虑采用多项式逼近。

（3）一些方程无法进行直线化转换，此时可直接采用最小二乘法拟合。所有曲线方程均可采用最小二乘法直接拟合，且一般预期可比线性化方法获得更好的拟合度。

2、指数曲线方程 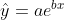$\hat{y}=ae^{bx}$ 的配置

若 y 观察值都大于 0，则可对两边取自然对数： $In\hat{y}=Ina+bx$

令 ${y}'=Iny$ , 则 ${\hat{y}}'=Ina+bx$

${y}'$ 与 x 的线性相关系数： $r_{y'x}=\frac{SP_{y'x}}{\sqrt{SS_{x}\cdot SS_{{y}'}}}$

若显著， $b=SP_{y'x}/SS_{x}$

$Ina={\bar{y}}'-b\bar{x}$

$a=e^{Ina}$

3、幂函数曲线方程 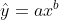$\hat{y}=ax^{b}$ 的配置

若 y 和 x 都大于0时可线性化： $In\hat{y}=Ina+bInx$

令 ${y}'=Iny$ , ${x}'=Inx$ , 则 ${\hat{y}}'=Ina+b{x}'$

${y}'$ 与 x 的线性相关系数： $r_{y'x'}=\frac{SP_{y'x'}}{\sqrt{SS_{{x}'}\cdot SS_{{y}'}}}$

若显著， $b=SP_{y'x'}/SS_{x'}$

$Ina={\bar{y}}'-b\bar{x}'$

$a=e^{Ina}$

4、Logistic曲线方程的配置

$\hat{y}=\frac{k}{1+ae^{-bx}}$ (a、b、k均大于0)

要对方程进行线性化处理，必须首先确定k值。

根据k是生长过程中的终极量的特点，有两种方法估计：

（1）如果y是累积频率，k=100%

（2）如果y是生长量或繁殖量，可取3对观察值 $(x_{1},y_{1})$ , $(x_{2},y_{2})$ , $(x_{3},y_{3})$ 分别带入方程得到联立方程：

$y_{1}=\frac{k}{1+ae^{-bx_{1}}}$

$y_{2}=\frac{k}{1+ae^{-bx_{2}}}$

$y_{3}=\frac{k}{1+ae^{-bx_{3}}}$

令 $x_{2}=(x_{1}+x_{3})/2$ ,则可解得: $k=\frac{y_{2}^{2}(y_{1}+y_{3})-2y_{1}y_{2}y_{3}}{y_{2}^{2}-y_{1}y_{3}}$

有了 k 的估值后，将方程移项并取自然对数得：

$In\left ( \frac{k-\hat{y}}{\hat{y}}\right )=Ina-bx$

令 ${y}'=In\left ( \frac{k-y}{y}\right )$ ,可得直线回归方程： ${\hat{y}}'=Ina-bx$

y和x对于Logistic方程的符合度可由 ${y}'$ 和x的相关系数给出： $r_{y'x}=\frac{SP_{y'x}}{\sqrt{SS_{x}\cdot SS_{{y}'}}}$

若显著， $-b=SP_{y'x}/SS_{x}$

$Ina={\bar{y}}'+b\bar{x}$

$a=e^{Ina}$

多项式回归实际上只是多元回归的一种特殊情况。

对于线性模型（lm），调整后的R平方包含在summary（model）语句的输出中。AIC是通过其自己的函数调用AIC（model）生成的。使用将方差分析函数应用于两个模型进行额外的平方和检验。

对于AIC，越小越好。对于调整后的R平方，越大越好。将模型a与模型b进行比较的额外平方和检验的非显着p值表明，带有额外项的模型与缩小模型相比，并未显着减少平方误差和。也就是说，p值不显着表明带有附加项的模型并不比简化模型好。



Data = read.table(textConnection(Input),header=TRUE)


### Change Length from integer to numeric variable
###   otherwise, we will get an integer overflow error on big numbers

Data$Length = as.numeric(Data$Length)


### Create quadratic, cubic, quartic variables

library(dplyr)

Data = 
mutate(Data, 
       Length2 = Length*Length,
       Length3 = Length*Length*Length,
       Length4 = Length*Length*Length*Length)

library(FSA)

headtail(Data)

 

   Length Clutch Length2  Length3     Length4

1     284      3   80656 22906304  6505390336

2     290      2   84100 24389000  7072810000

3     290      7   84100 24389000  7072810000

16    323     13  104329 33698267 10884540241

17    334      2  111556 37259704 12444741136

18    334      8  111556 37259704 12444741136

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

定义要比较的模型

model.1 = lm (Clutch ~ Length,                               data=Data)
model.2 = lm (Clutch ~ Length + Length2,                     data=Data)
model.3 = lm (Clutch ~ Length + Length2 + Length3,           data=Data)
model.4 = lm (Clutch ~ Length + Length2 + Length3 + Length4, data=Data)

生成这些模型的模型选择标准统计信息

summary(model.1)

 

Coefficients:

            Estimate Std. Error t value Pr(>|t|)

(Intercept)  -0.4353    17.3499   -0.03     0.98

Length        0.0276     0.0563    0.49     0.63

 

Multiple R-squared:  0.0148,  Adjusted R-squared:  -0.0468

F-statistic: 0.24 on 1 and 16 DF,  p-value: 0.631

 

 

AIC(model.1)

 

[1] 99.133

 

 

summary(model.2)

 

Coefficients:

             Estimate Std. Error t value Pr(>|t|)  

(Intercept) -9.00e+02   2.70e+02   -3.33   0.0046 **

Length       5.86e+00   1.75e+00    3.35   0.0044 **

Length2     -9.42e-03   2.83e-03   -3.33   0.0045 **

 

Multiple R-squared:  0.434,   Adjusted R-squared:  0.358

F-statistic: 5.75 on 2 and 15 DF,  p-value: 0.014

 

 

AIC(model.2)

 

[1] 91.16157

 

 

anova(model.1, model.2)

 

Analysis of Variance Table

 

  Res.Df    RSS Df Sum of Sq      F  Pr(>F)  

1     16 186.15                              

2     15 106.97  1    79.178 11.102 0.00455 **

其余模型继续此过程

四个多项式模型的模型选择标准。模型2的AIC最低，表明对于这些数据，它是此列表中的最佳模型。同样，模型2显示了最大的调整后R平方。最后，额外的SS测试显示模型2优于模型1，但模型3并不优于模型2。所有这些证据表明选择了模型2。

AIC	调整后的R平方	p值
99.1	-0.047
91.2	0.36	0.0045
92.7	0.33	0.55
94.4	0.29	0.64

对比与方差分析

AIC，AICc或BIC中的任何一个都可以最小化以选择最佳模型。



 

$Fit.criteria

  Rank Df.res   AIC   AICc    BIC R.squared Adj.R.sq p.value Shapiro.W Shapiro.p

1    2     16 99.13 100.80 101.80   0.01478  -0.0468 0.63080    0.9559    0.5253

2    3     15 91.16  94.24  94.72   0.43380   0.3583 0.01403    0.9605    0.6116

3    4     14 92.68  97.68  97.14   0.44860   0.3305 0.03496    0.9762    0.9025

4    5     13 94.37 102.00  99.71   0.45810   0.2914 0.07413    0.9797    0.9474

 

 

  Res.Df    RSS Df Sum of Sq       F   Pr(>F)  

1     16 186.15                                

2     15 106.97  1    79.178 10.0535 0.007372 **  ## Compares m.2 to m.1

3     14 104.18  1     2.797  0.3551 0.561448     ## Compares m.3 to m.2

4     13 102.38  1     1.792  0.2276 0.641254     ## Compares m.4 to m.3

最受欢迎的见解

1.R语言多元Logistic逻辑回归应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

研究最终模型



Coefficients:

             Estimate Std. Error t value Pr(>|t|)  

(Intercept) -9.00e+02   2.70e+02   -3.33   0.0046 **

Length       5.86e+00   1.75e+00    3.35   0.0044 **

Length2     -9.42e-03   2.83e-03   -3.33   0.0045 **

 

Multiple R-squared:  0.434,   Adjusted R-squared:  0.358

F-statistic: 5.75 on 2 and 15 DF,  p-value: 0.014

 

 

 

Anova Table (Type II tests)

 

Response: Clutch

          Sum Sq Df F value Pr(>F)  

Length      79.9  1    11.2 0.0044 **

Length2     79.2  1    11.1 0.0045 **

Residuals  107.0 15

模型的简单图解

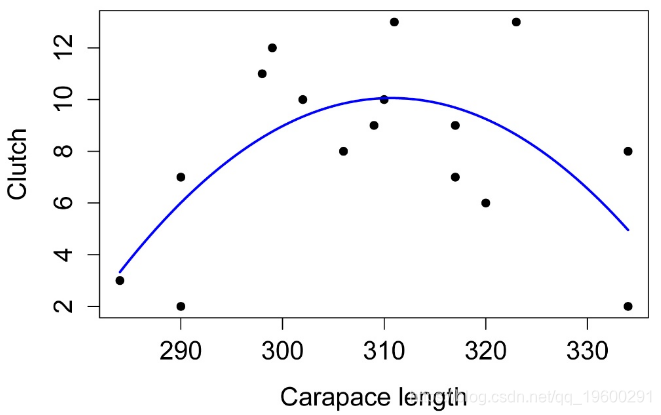
检查模型的假设

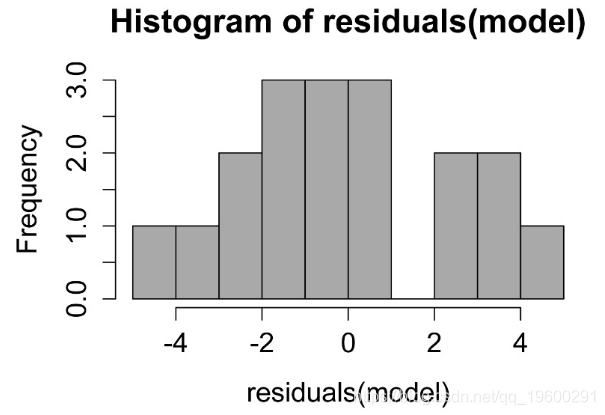
线性模型中残差的直方图。这些残差的分布应近似正态。

残差与预测值的关系图。残差应无偏且均等。

###通过以下方式检查其他模型：

具有多项式样条的B样条回归

B样条回归使用线性或多项式回归的较小部分。它不假设变量之间存在线性关系，但是残差仍应是独立的。该模型可能会受到异常值的影响。

### --------------------------------------------------------------
### B-spline regression, turtle carapace example
 ### --------------------------------------------------------------


summary(model)                         # Display p-value and R-squared

 

Residual standard error: 2.671 on 15 degrees of freedom

Multiple R-squared:  0.4338,  Adjusted R-squared:  0.3583

F-statistic: 5.747 on 2 and 15 DF,  p-value: 0.01403

模型的简单图解

检查模型的假设

线性模型中残差的直方图。这些残差的分布应近似正态。

残差与预测值的关系图。残差应无偏且均等。

非线性回归

非线性回归可以将各种非线性模型拟合到数据集。这些模型可能包括指数模型，对数模型，衰减曲线或增长曲线。通过迭代过程，直到一定的收敛条件得到满足先后找到更好的参数估计。

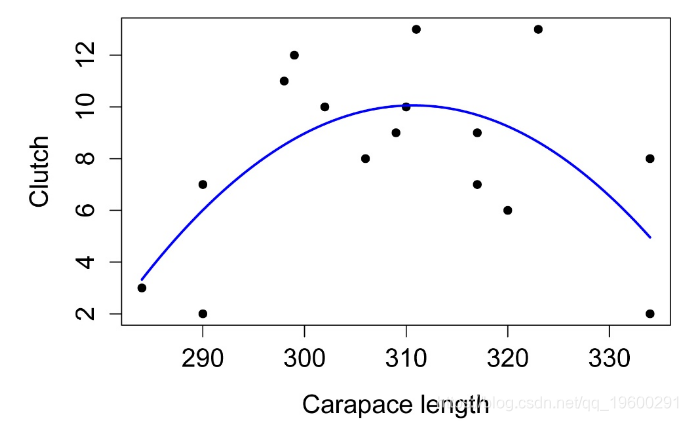
在此示例中，我们假设要对数据拟合抛物线。

数据中包含变量（Clutch和Length），以及我们要估计的参数（Lcenter，Cmax和a）。

没有选择参数的初始估计的固定过程。通常，参数是有意义的。这里Lcenter 是顶点的x坐标，Cmax是顶点的y坐标。因此我们可以猜测出这些合理的值。尽管我们知道参数a应该是负的，因为抛物线向下打开。

因为nls使用基于参数初始估计的迭代过程，所以如果估计值相差太远，它将无法找到解决方案，它可能会返回一组不太适合数据的参数估计。绘制解决方案并确保其合理很重要。

如果您希望模型具有整体p值，并且模型具有伪R平方，则需要将模型与null模型进行比较。从技术上讲，要使其有效，必须将null模型嵌套在拟合模型中。这意味着null模型是拟合模型的特例。

对于没有定义r平方的模型，已经开发了各种伪R平方值。

### --------------------------------------------------------------
### Nonlinear regression, turtle carapace example
### --------------------------------------------------------------


Data = read.table(textConnection(Input),header=TRUE)



 

Parameters:

         Estimate Std. Error t value Pr(>|t|)   

Lcenter 310.72865    2.37976  130.57  < 2e-16 ***

Cmax     10.05879    0.86359   11.65  6.5e-09 ***

a        -0.00942    0.00283   -3.33   0.0045 **

确定总体p值和伪R平方



anova(model, model.null)

 

  Res.Df Res.Sum Sq Df  Sum Sq F value  Pr(>F) 

1     15     106.97                            

2     17     188.94 -2 -81.971   5.747 0.01403 *

 

 

$Pseudo.R.squared.for.model.vs.null

                             Pseudo.R.squared

McFadden                             0.109631

Cox and Snell (ML)                   0.433836

Nagelkerke (Cragg and Uhler)         0.436269

确定参数的置信区间




              2.5 %        97.5 %
Lcenter 305.6563154 315.800988774
Cmax      8.2180886  11.899483768
a        -0.0154538  -0.003395949




------
Bootstrap statistics
            Estimate  Std. error
Lcenter 311.07998936 2.872859816
Cmax     10.13306941 0.764154661
a        -0.00938236 0.002599385

------
Median of bootstrap estimates and percentile confidence intervals
               Median         2.5%         97.5%
Lcenter 310.770796703 306.78718266 316.153528168
Cmax     10.157560932   8.58974408  11.583719723
a        -0.009402318  -0.01432593  -0.004265714

模型的简单图解

检查模型的假设

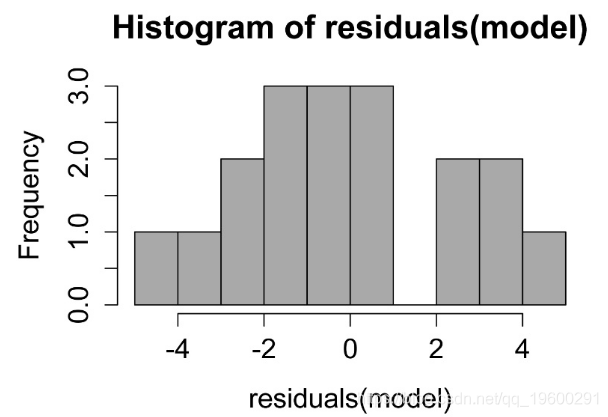
线性模型中残差的直方图。这些残差的分布应近似正态。


plot(fitted(model), 
     residuals(model))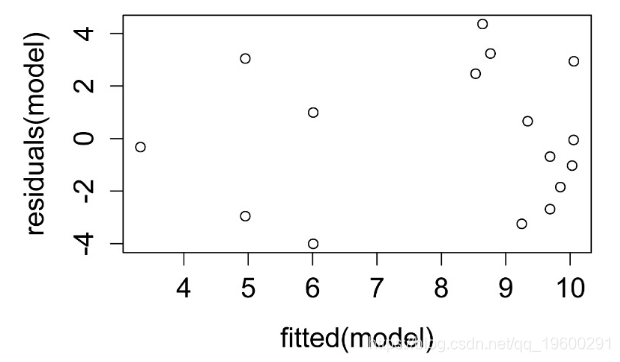

残差与预测值的关系图。残差无偏且均等。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言曲线回归：多项式回归、多项式样条回归、非线性回归数据分析

多项式回归

两个变数呈现曲线关系的回归称曲线回归（curvilinear regression）或非线性回归（non-linear regression）。

以最小二乘法分析曲线关系资料在数量变化上的特征和规律，称为曲线回归分析或非线性回归分析。

曲线角度看，线性回归仅是其中的一个特例：直线可看成是曲率为0的曲线。

一、曲线的类型与特点

（1）指数函数曲线

（2）对数函数曲线

（3）幂函数曲线

（4）双曲函数曲线：变形双曲线

（5）S型曲线

二、曲线方程的配置

1、曲线回归分析的一般程序

2、指数曲线方程 的配置

3、幂函数曲线方程 的配置

4、Logistic曲线方程的配置

对比与方差分析

具有多项式样条的B样条回归

非线性回归

相关文章

关注有关新文章的微信公众号

2、指数曲线方程 $\hat{y}=ae^{bx}$ 的配置

3、幂函数曲线方程 $\hat{y}=ax^{b}$ 的配置