方差分析是一种常见的统计模型，顾名思义，方差分析的目的是比较平均值。
为了说明该方法，让我们考虑以下样例，该样例为学生在硕士学位课程中的最终统计考试成绩（分数介于0到20之间）。
成绩是我们的变量 X。“分组”变量是学生参加辅导课的方式，采用“自愿参与”，“非自愿参与”的方式，最后是“不参与”（不参加或拒绝参加的学生）。
为了进行分组，我们有两个变量。
第一个分组变量是学生的性别（“ F”和“ M”），第二个分组变量是学生的身份（取决于他们是否获得许可）。
方差分析原理
对总体均值的假设检验，有三种情况：
1、总体均值与某个常数进行比较；
2、两个总体均值之间的比较；
3、两个以上总体均值之间的比较；
对于前两种情况，用Z分布和T分布就能快速得到假设检验结果。如果比较的总体大于三个，继续用它们也能够得到比较结果，只是需要两两比较，耗时耗力。这种情况下，使用方差分析能够一次性比较两个及两个以上的总体均值，看看它们之间是否有显著性差异。常用的方差分析方法包括：单因素方差分析、多因素方差分析、协方差分析、多元方差分析、重复测量方差分析、方差成分分析等。
方差分析原理
方差分析的原理通俗的解释就是将试验数据的总离散分解为来源于不同因素的离散，并作出数据估计，从而发现各个因素在总离散中所占的重要程度。
名词解释
因素：方差分析的研究变量；例如，研究裁判打分的差异，裁判就被称为因素；
水平：因素中的内容称为水平；例如，总共有3个裁判打分，则裁判因素的水平就是3；
观测因素：又称观测变量，指对影响总体的因素；
控制因素：又称控制变量，指影响观测变量的因素；
假设检验原理
以单因素方差分析为例，介绍方差分析原理，下图是单因素方差分析表格。
如果单个因素的不同水平对于数据总体没有影响，那么组间方差与组内方差没有显著性差异；如果单个因素的不同水平对于数据总体有影响，组间方差和组内方差就会有显著性的差异。用组间方差除以组内方差，得到F值，F值的分布服从F分布，所以F值在F分布上有对应的显著概率p值。当p值大于假设检验的显著性水平时，说明组间方差和组内方差没有显著性差异，也就是说因素的不同水平对于数据总体没有影响；反之，当p值小于假设检验的显著性水平，说明因素的不同水平对于数据总体有影响。
假定条件
1、多个样本来自的多个总体是正态分布的。方差分析运用的是F分布，只有服从正态分布的总体才适用F分布进行假设检验，否则，检验结果是没有意义的。
2、单个因素的不同水平分组的方差要求齐性。前面介绍了，方差分析假设的是单个因素的不同分组数据之间没有区别，换一种说法就是单个因素的不同分组对于数据总体没有影响，也就是说不同分组的数据都来自同一个数据总体，方差相同。
基于以上两个假设，方差分析才能将方差的差异性推断转换成对两个以上总体均值的差异性推断。
事后多重比较
经过方差分析以后，如果检验结果显示多个水平之间存在显著性差异，那么还需要进行事后多重比较。因为方差分析结果的显著只能说明两个以上总体的均值之间存在显著性，但是不能分析出具体是那几个总体的均值不相等，所以还需要进行两两总体均值的比较。
方差分析步骤
1、方差齐性减压；
2、计算各项平方和与自由度；
3、列出方差分析表，进行F检验，并依据F值对应的p值做出判断；
4、事后多重比较；
方差分析模型
方差分析的基本思路是将数据波动（变异）分解为若干部分，除了有一部分代表随机误差，其余每个部分的变异分别代表了某个影响因素的作用(包括交互作用形成的因素)。通过比较因素所致的变异与随机误差的大小，借助F分布和F统计量做出推断：该因素对因变量的影响是否显著存在。F统计量=组间方差/组内方差。
首先，我们 简单浏览一下数据
> tail(base)
PART GEN ORIG NOTE
112 vol F R1 16.50
113 non_vol. M R1 11.50
114 non_vol. F R1 10.25
115 non_vol. F R1 10.75
116 non_vol. F a 10.50
117 vol M R1 15.75我们浏览了数据的最后六行。
在开始多因素分析之前，让我们从单因素分析开始。我们可以查看分数的变化，具体取决于分组变量
> boxplot(base$NOTE~base$PAR
> abline(h=mean(base$NOTE),lty=2,col="re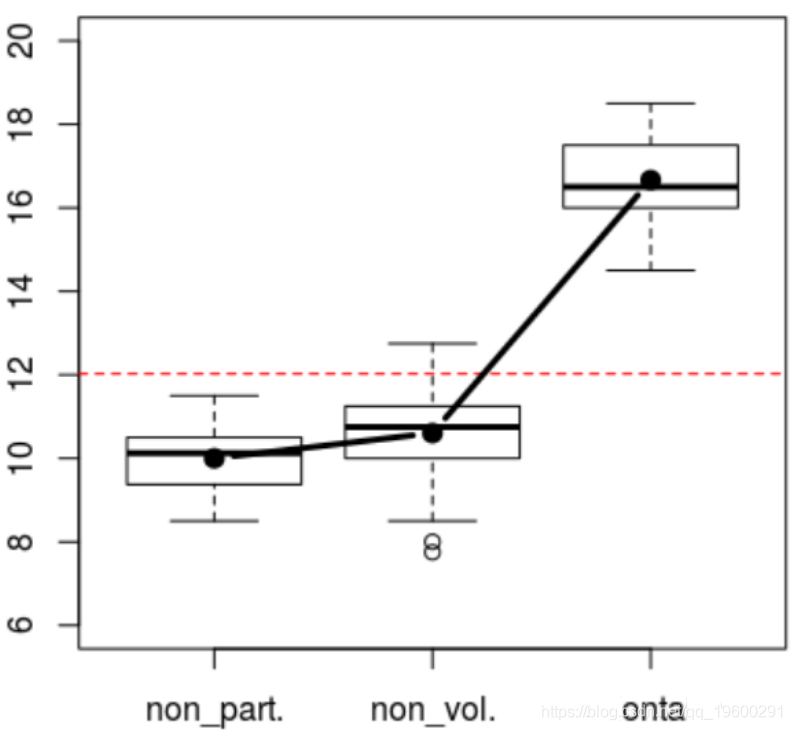
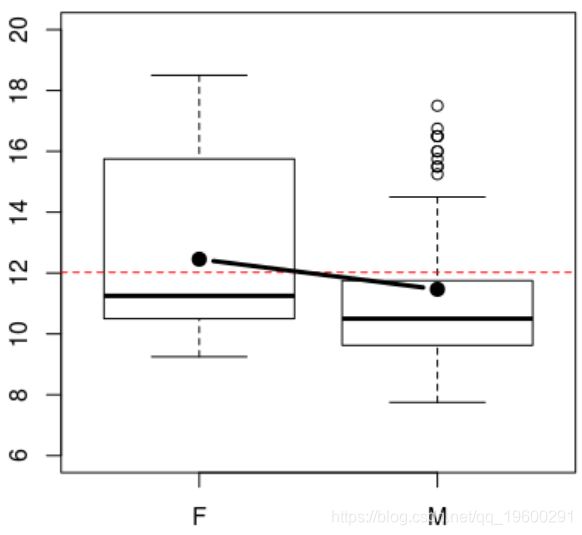
我们还可以根据性别来查看
> boxplot(NOTE~GEN,ylim=c(6,20))
在方差分析中，假设 ，
指定可能的处理方式（这里有3种）。
我们将考虑对 作为补充假设
。然后，我们将估计两个模型。
第一个是约束模型。
> sum(residuals(lm(NOTE~1,data=base))^2)
[1] 947.4979对应于
> (SCR0=sum((base$NOTE-mean(base$NOTE))^2))
[1] 947.4979第二，我们进行回归，
> sum(residuals(lm(NOTE~PART,data=base))^2)
[1] 112.5032当我们与子组的平均值进行比较时，就等于查看了误差，
> sum(residuals(lm(NOTE~PART,data=base))^2)
[1] 112.5032费舍尔的统计数据
> (F=(SCR0-SCR1)*(nrow(base)-3)/SCR1/(3-1))
[1] 423.0518判断我们是否处于接受或拒绝假设的范围内 ，可以看一下临界值，它对应于费舍尔定律的95％分位数，
> qf(.95,3-1,nrow(base)-3)
[1] 3.075853由于远远超过了这个临界值，我们拒绝 。我们还可以计算p值
> 1-pf(F,3-1,nrow(base)-3)
[1] 0在这里（通常）为零。它对应于我们通过函数得到的
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 423.05 < 2.2e-16 ***
Residuals 114 112.50 0.99
---或者
Terms:
PART Residuals
Sum of Squares 834.9946 112.5032
Deg. of Freedom 2 114
Residual standard error: 0.9934135
Estimated effects may be unbalanced可以总结为
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 423.05 < 2.2e-16 ***
Residuals 114 112.50 0.99
---我们在这里可以看到分数并非独立于分组变量。
我们可以进一步挖掘。Tukey检验提供“多重检验”，它将成对地查看均值的差异，
Tukey multiple comparisons of means
95% family-wise confidence level
$PART
diff lwr upr p adj
non_vol.-non_part. 0.60416 -0.04784 1.2561 0.07539
volontaire-non_part. 6.66379 5.92912 7.3984 0.00000
volontaire-non_vol. 6.05962 5.54078 6.5784 0.00000我们在这里看到，“非自愿”和“非参与”之间的差异不显着为非零。或更简单地说，假设我们将接受零为零的假设。另一方面，“自愿”参加的得分明显高于“非自愿”参加或不参加的得分。我们还可以成对查看学生的检验，
Pairwise comparisons using t tests with pooled SD
data: NOTE and PART
non_part. non_vol.
non_vol. 0.03 -
volontaire <2e-16 <2e-16如果我们将“非自愿”和“非参与”这两种方式结合起来，并将这种方式与“自愿”方式进行比较，我们最终将对平均值进行检验，
Welch Two Sample t-test
data: NOTE[PART == "volontaire"] and NOTE[PART != "volontaire"]
t = 29.511, df = 50.73, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
5.749719 6.589231
sample estimates:
mean of x mean of y
16.66379 10.49432我们看到，我们在这里接受了“志愿者”学生的成绩与其他学生不同的假设。
在继续之前，请记住在模型中
在某种意义上说，与对应于同调模型
不依赖分组
。
我们可以使用Bartlett检验（该检验将检验方差的同质性）来检验该假设，请记住，如果p值超过5％，则假设“方差齐整性”得到了验证
Bartlett test of homogeneity of variances
data: base$NOTE and base$PART
Bartlett's K-squared = 0.5524, df = 2, p-value = 0.7587更进一步，我们可以尝试对性别进行方差分析的两因素分析，通常要根据我们的分组情况，也可以根据性别对变量进行分析。当均值的形式为零时，我们将讲一个没有相互作用的模型 ，我们可以包括我们考虑的交互
总的来说，我们的模型
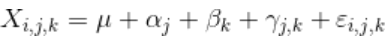
其中，按实验处理方式表示与观察到的平均值平均值的偏差，而按组表示与所观察到的平均值平均值的偏差。这样可以通过添加一些约束来识别模型。最大似然估计：
对应于总体平均值
对应于每次实验的平均值（或更确切地说，它与总体平均值的偏差），
最后
是
我们对一组进行方差分析
对于约束模型，
和
表示实验次数和组数
方差分解公式在这里给出
我们将进行手动计算，
Terms:
PART GENRE PART:GENRE Residuals
Sum of Squares 834.9946 20.9618 3.4398 88.1017
Deg. of Freedom 2 1 2 111
Residual standard error: 0.8909034
Estimated effects may be unbalanced总结结果
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 526.0081 < 2.2e-16 ***
GENRE 1 20.96 20.96 26.4099 1.194e-06 ***
PART:GENRE 2 3.44 1.72 2.1669 0.1194
Residuals 111 88.10 0.79
---由于实验组与对照组之间似乎没有任何交互作用，因此可以将其从方差分析中删除。
Analysis of Variance Table
Response: NOTE
Df Sum Sq Mean Sq F value Pr(>F)
PART 2 834.99 417.50 515.364 < 2.2e-16 ***
GENRE 1 20.96 20.96 25.875 1.461e-06 ***
Residuals 113 91.54 0.81
---从结果可以看到（自愿）参加课程会有所帮助。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】Python比赛LightGBM、XGBoost+GPU和CatBoost预测学生在游戏学习过程表现|数据代码分享
WEKA关联规则挖掘Apriori算法在学生就业数据中的应用
R语言分析糖尿病数据：多元线性模型、MANOVA、决策树、典型判别分析、HE图、Box’s M检验可视化
