本文将介绍R中可用于投资组合优化的不同求解器。
通用求解器可以处理任意的非线性优化问题,但代价是收敛速度慢。
通用求解器
默认包
包stats(默认安装的基本R包)提供了几个通用的优化程序。
- optimize()。用于区间内的一维无约束函数优化(对于一维求根,使用uniroot())。
可下载资源
f <- function(x) exp(-0.5*x) * sin(10*pi*x)
f(0.5)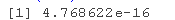
非线性规划指的是目标函数 是非线性函数,或者约束集
是由非线性的等式和不等式给定的优化问题。一直以来,优化理论和方法都在工程实践以及管理决策等方面有着重要的应用,例如近年来如日中天的机器学习方法中,对loss function的的优化的梯度下降方法和牛顿方法等都是优化理论中的经典方法。
我们首先来看下面一个问题:
这是一个简单的函数最小化问题,决策变量 可以是离散或者连续的,其可行域为
,当目标函数
是一个非线性函数时候这就是一个非线性优化问题,那么如果要求解这个问题我们需要哪些条件呢?
最优性条件
我们在高中的时候都学过导数的概念,对于一个复杂函数可以通过对其求导的方式求解其极值,在这里我们将极值的概念进一步扩展。
在这里我们首先讨论无约束情况下的优化问题
局部最小值和全局最小值
当向量 是
的一个无约束局部最小值点,那么在该点处的邻域内存在
满足:
在这里 为欧式范数,即n维向量空间上的距离。
而当向量 被称作
无约束的全局最小值点,是指该点的函数值不大于其他所有点的函数值,即满足:
最优性的必要条件
如果目标函数是可微的,那么我们可以利用梯度和泰勒展开来探索最优性的必要条件,首先我们假定某个向量 的一个微小梯度为
,那么根据一阶的泰勒展开我们可以得到:
如果 是一个无约束的局部最小值点,那么我们可以得到:
在这里因为 是可正可负的,所以我们可以得到
以及
,很显然我们得到了最优性的第一个条件–一阶导数为0:
现在我们接着进行二阶泰勒展开:
应用第一个条件的结论我们可以得到 ,因此可知
必定是半正定的。
综上可知最优性的必要条件为: 且
。
result <- optimize(f, interval = c(0, 1), tol = 0.0001)
result

# 绘制
curve(0, 1, n = 200)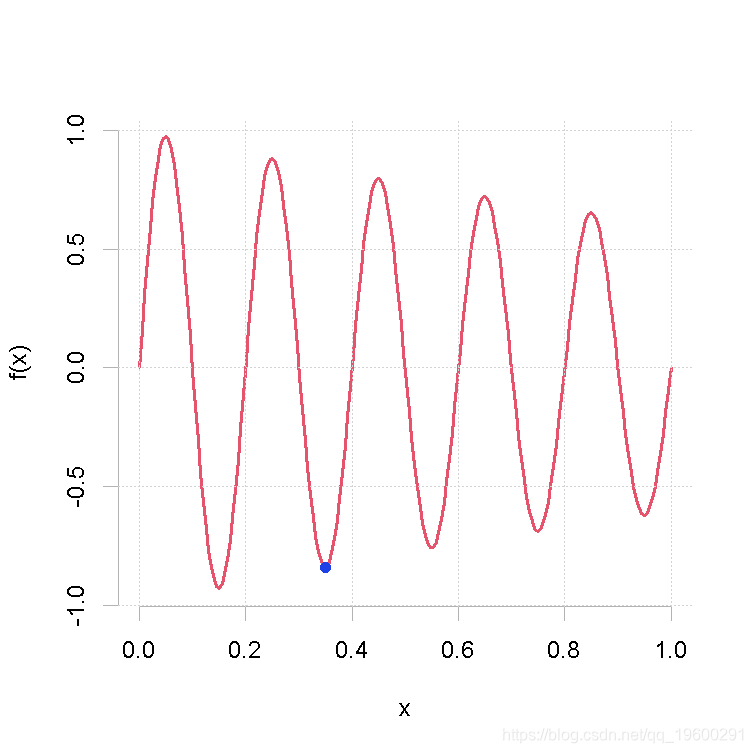
optim()通用优化,有六种不同的优化方法。Nelder-Mead:相对稳健的方法(默认),不需要导数。CG:适用于高维无约束问题的低内存优化BFGS:简单的无约束的准牛顿方法L-BFGS-B:用于边界约束问题的优化SANN: 模拟退火法Brent: 用于一维问题(实际上是调用optimize())。
这个例子做了一个最小二乘法拟合:最小化
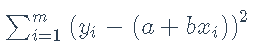
# 要拟合的数据点
# 线性拟合的l2-norm误差平方 y ~ par[1] + par[2]*x
# 调用求解器(初始值为c(0, 1),默认方法为 "Nelder-Mead")。
optim(par = c(0, 1), f, data = dat)
# 绘制线性回归图
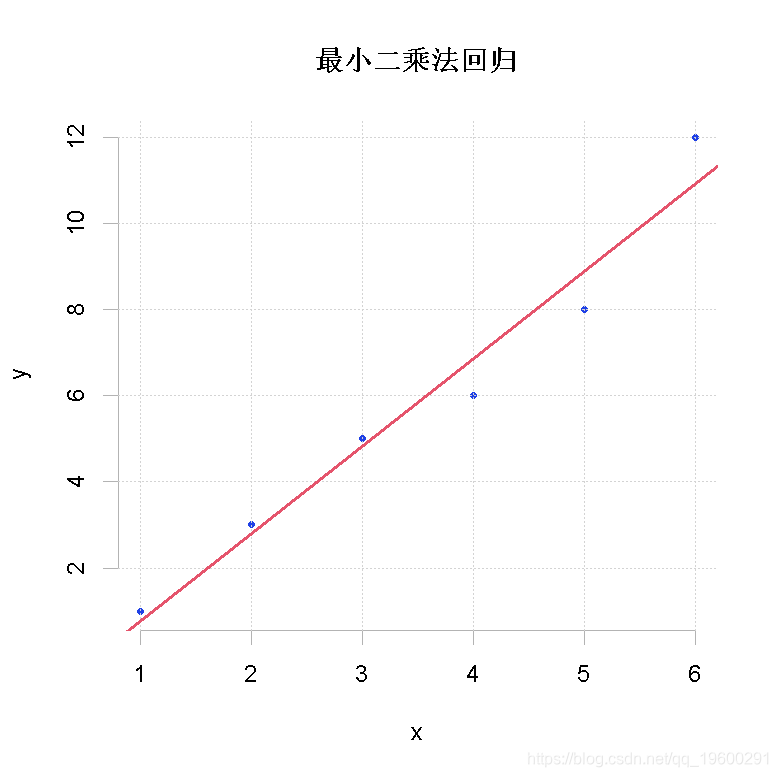
# 与R中内置的线性回归进行比较
lm(y ~ x, data = dat)
下一个例子说明了梯度的使用,著名的Rosenbrock香蕉函数:
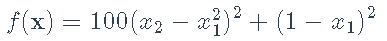
,梯度
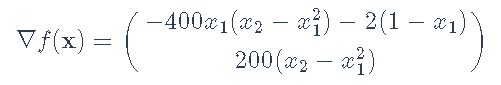
,无约束最小化问题
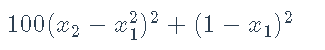
# Rosenbrock香蕉函数及其梯度
banana <- function(x)
c(-400 * x[1] * (x[2] - x[1] * x[1]) - 2 * (1 - x[1]),
200 * (x[2] - x[1] * x[1]))
optim(c(-1.2, 1), f_banana)
Rosenbrock香蕉函数及其梯度
banana <- function(x)
c(-400 x[1] (x[2] - x[1] x[1]) - 2 (1 - x[1]),
200 (x[2] - x[1] x[1]))
optim(c(-1.2, 1), f_banana)
optim(c(-1.2, 1), f, gr, method = "BFGS")
下面的例子使用了界约束。
最小化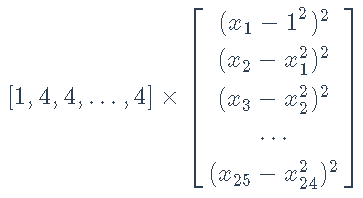
约束: 
p <- length(x); sum(c(1, rep(4, p-1)) * (x - c(1, x[-p])^2)^2) }
# 25维度约束
optim(rep(3, 25), f,lower = rep(2, 25), upper = rep(4
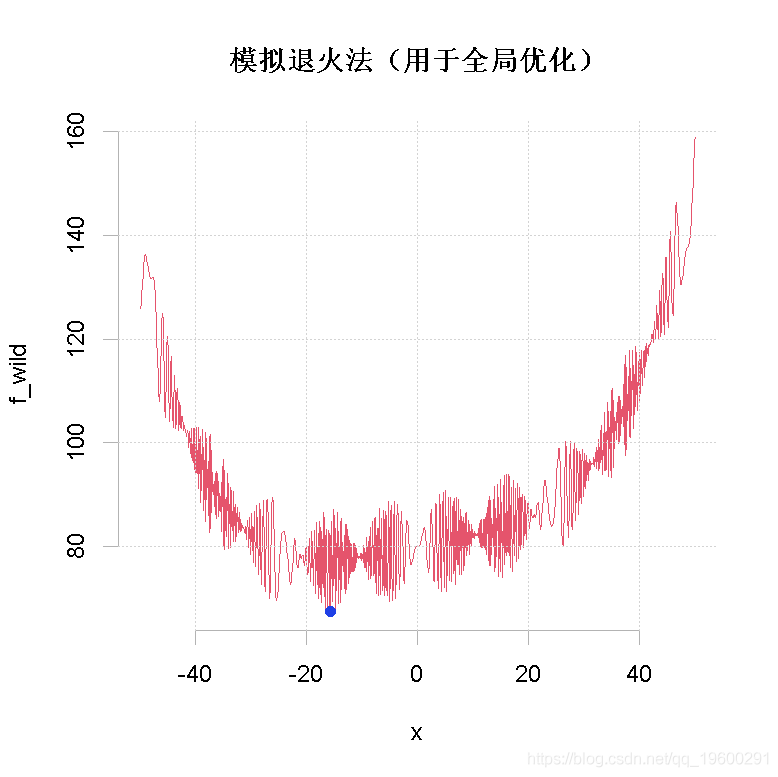
这个例子使用模拟退火法(用于全局优化)。
#全局最小值在-15左右
res <- optim(50, f, method = "SANN")

# 现在进行局部改进(通常只改进了一小部分)
optim(res$par, f , method = "BFGS")
- constrOptim()。使用自适应约束算法,在线性不等式约束下最小化一个函数(调用optim())。
随时关注您喜欢的主题
# 不等式约束(ui %*% theta >= ci): x <= 0.9, y - x > 0.1
constrOptim(c(.5, 0) 
nlm(): 这个函数使用牛顿式算法进行目标函数的最小化。
nlm(f, c(10,10))

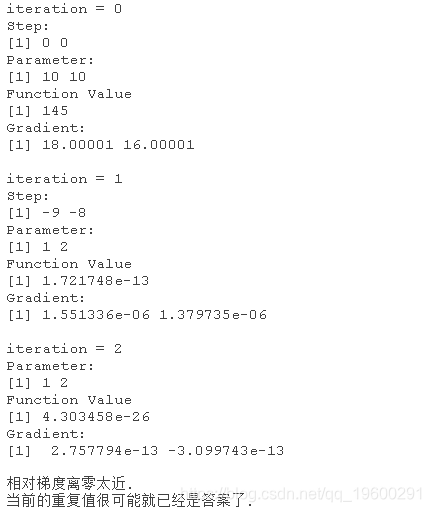
nlminb(): 进行无界约束优化。.
nlminb(c(-1.2, 1), f)

nlminb(c(-1.2, 1), f, gr)

optim
基础函数optim()作为许多其他求解器的包,可以方便地使用和比较。

# opm() 可以同时使用几个方法
opm( f , method = c("Nelder-Mead", "BFGS"))
全局优化
全局优化与局部优化的理念完全不同(全局优化求解器通常被称为随机求解器,试图避免局部最优点)。
特定类别问题的求解器
如果要解决的问题属于某一类问题,如LS、LP、MILP、QP、SOCP或SDP,那么使用该类问题的专用求解器会更好。
最小二乘法 (LS)
线性最小二乘法(LS)问题是将 最小化,可能有界或线性约束。
最小化,可能有界或线性约束。
线性规划(LP)
函数solveLP(),可以方便地解决以下形式的LP:
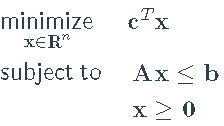
#> 加载所需软件包
cvec <- c(1800, 600, 600) # 毛利率
bvec <- c(40, 90, 2500) # 捐赠量
# 运行求解器
solveLP(maximum = TRUE)#> 加载所需软件包cvec <- c(1800, 600, 600) # 毛利率
bvec <- c(40, 90, 2500) # 捐赠量# 运行求解器
solveLP(maximum = TRUE)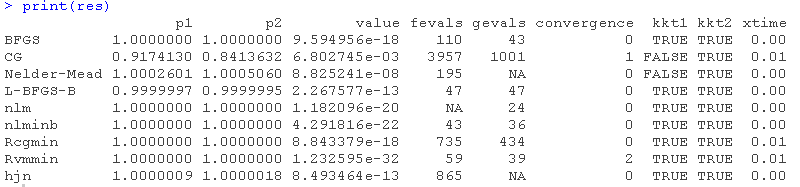
lpSolve(比linprog快得多,因为它是用C语言编码的)可以解决线性混合整数问题(可能带有一些整数约束的LP)。
混合整数线性规划 (MILP)
# 设置问题:
# maximize x1 + 9 x2 + x3
# subject to x1 + 2 x2 + 3 x3 <= 9
# 3 x1 + 2 x2 + 2 x3 <= 15
# 运行求解
res <- lp("max", f, con)
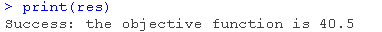
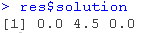
# 再次运行,这次要求三个变量都是整数
lp( int.vec = 1:3)
solution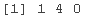
二次规划 (QP)
可以方便地解决以下形式的QP
# 设置问题: # minimize -(0 5 0) %*% x + 1/2 x^T x # subject to A^T x >= b # with b = (-8,2,0)^T # (-4 2 0) # A = (-3 1 -2) # ( 0 0 1) #运行求解 solve(Dmat,...)
解决具有绝对值约束和目标函数中的绝对值的二次规划。
二阶锥规划 (SOCP)
有几个包:
- ECOSolveR提供了一个与嵌入式COnic Solver(ECOS)的接口,这是一个著名的、高效的、稳健的C语言库,用于解决凸问题。
- CLSOCP提供了一个用于解决SOCP问题的一步平滑牛顿方法的实现。
优化基础
我们已经看到了两个包,它们是许多其他求解器的包。
用于凸问题、MIP和非凸问题
ROI包为处理R中的优化问题提供了一个框架。它使用面向对象的方法来定义和解决R中的各种优化任务,这些任务可以来自不同的问题类别(例如,线性、二次、非线性规划问题)。
LP – 考虑 LP:
最大化:
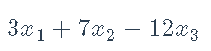
约束:
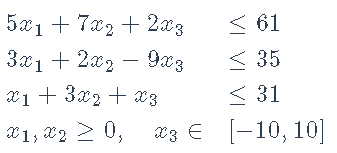
#> ROI: R 优化基础设施
#> 求解器插件: nlminb, ecos, lpsolve, scs.
#> 默认求解器: auto.
OP(objective = L_objective(c(3, 7, -12)),...,
maximum = TRUE)
#> 投资回报率优化问题:
# 让我们来看看可用的求解器
# solve it
res <- ROI_solve(prob)
res
MILP – 考虑先前的LP,并通过添加约束条件x2,x3∈Z使其成为一个MILP.
# 只需修改之前的问题
types(prob) <- c("C", "I", "I")
prob
BLP – 考虑二元线性规划 (BLP):
最小化:
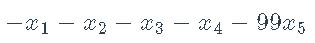
约束:
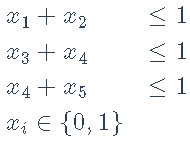
OP(objective = L_objective,..., ,
types = rep("B", 5))
ROI_solve(prob)
#> Optimal solution found.
#> The objective value is: -1.01e+02SOCP – 考虑SOCP:
最大化: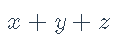
约束: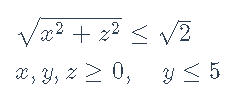
并注意到SOC约束 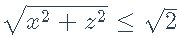 可以写成
可以写成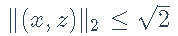 或
或 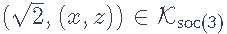 ,在代码中实现为:
,在代码中实现为: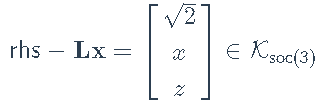 。
。
OP(objective = L_objective,...,
maximum = TRUE)
SDP–考虑SDP:
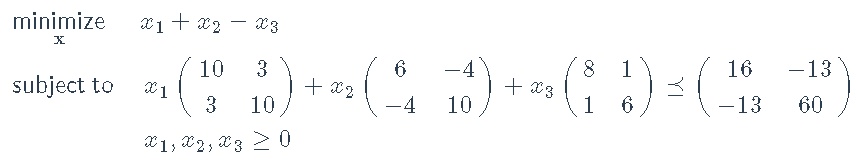
并注意SDP约束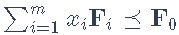 可以写成
可以写成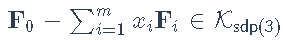 (大小为3是因为在我们的问题中,矩阵为2×2,但vech()提取了3个独立变量,因为矩阵是对称的)。
(大小为3是因为在我们的问题中,矩阵为2×2,但vech()提取了3个独立变量,因为矩阵是对称的)。
OP(objective = L_objective,...,
rhs ))
NLP – 考虑非线性规划(NLP)
最大化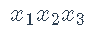 约束
约束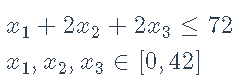 。
。
sum(huber(y - X %*% beta, M)
Problem(Minimize(obj))
solve(prob)弹性网正则化 – 我们现在要解决的问题是:最小化
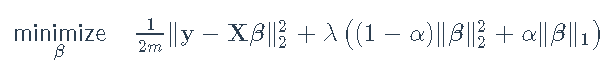
# 定义正则化项
elastic<- function(beta) {
ridge <- (1 - alpha) * sum(beta^2)
lasso <- alpha * p_norm(beta, 1)
# 定义问题并解决它
sum((y - X %*% beta)^2) + elastic(beta, lambda, alpha)
Problem(Minimize(obj))
solve(prob)稀疏逆协方差矩阵–考虑矩阵值的凸问题:最大化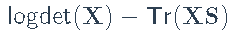 ,条件是
,条件是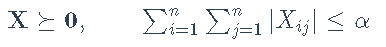
log\_det(X) - matrix\_trace(X %*% S)
list(sum(abs(X)) <= alpha)协方差–考虑矩阵值的凸问题:在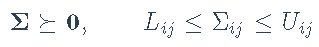 的条件下,最大化
的条件下,最大化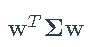 。
。
constr <- list(Sigma\[1,1\] == 0.2, Sigma\[1,2\] >= 0, Sigma\[1,3\] >= 0,
Sigma\[2,2\] == 0.1, Sigma\[2,3\] <= 0, Sigma\[2,4\] <= 0,
Sigma\[3,3\] == 0.3, Sigma\[3,4\] >= 0, Sigma\[4,4\] == 0.1)投资组合优化–考虑马科维茨投资组合设计:最大化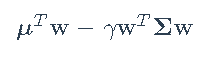 ,
,
Problem(Maximize(obj), constr)
solve(prob)结论
R语言中可用的求解器的数量很多。建议采取以下步骤。
- 如果是凸优化问题,那么开始进行初步测试。
- 如果速度不够快,使用ROI。
- 如果仍然需要更快的速度,那么如果问题属于定义好的类别之一,则使用该类别专用的求解器(例如,对于LP,推荐使用lpSolve,对于QP则使用quadprog)。
- 然而,如果问题不属于任何类别,那么就必须使用非线性优化的一般求解器。在这个意义上,如果一个局部的解决方案就够了,那么可以用许多求解器的包。如果需要全局求解器,那么软件包gloptim是一个不错的选择,它是许多全局求解器的包。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 专题:2025游戏行业全景报告:VC投资、AI应用、用户行为|附200+份报告PDF、数据、可视化模板汇总下载
专题:2025游戏行业全景报告:VC投资、AI应用、用户行为|附200+份报告PDF、数据、可视化模板汇总下载 专题:2025年游戏市场洞察报告:市场规模、用户行为、投资趋势|附320+份报告PDF、数据、可视化模板汇总下载
专题:2025年游戏市场洞察报告:市场规模、用户行为、投资趋势|附320+份报告PDF、数据、可视化模板汇总下载



