环境科学中的许多数据不适合简单的线性模型，最好用广义相加模型（GAM）来描述。
这基本上就是具有 光滑函数的广义线性模型（GLM）的扩展 。
当然，当您使用光滑项拟合模型时，可能会发生许多复杂的事情，但是您只需要了解基本原理即可。
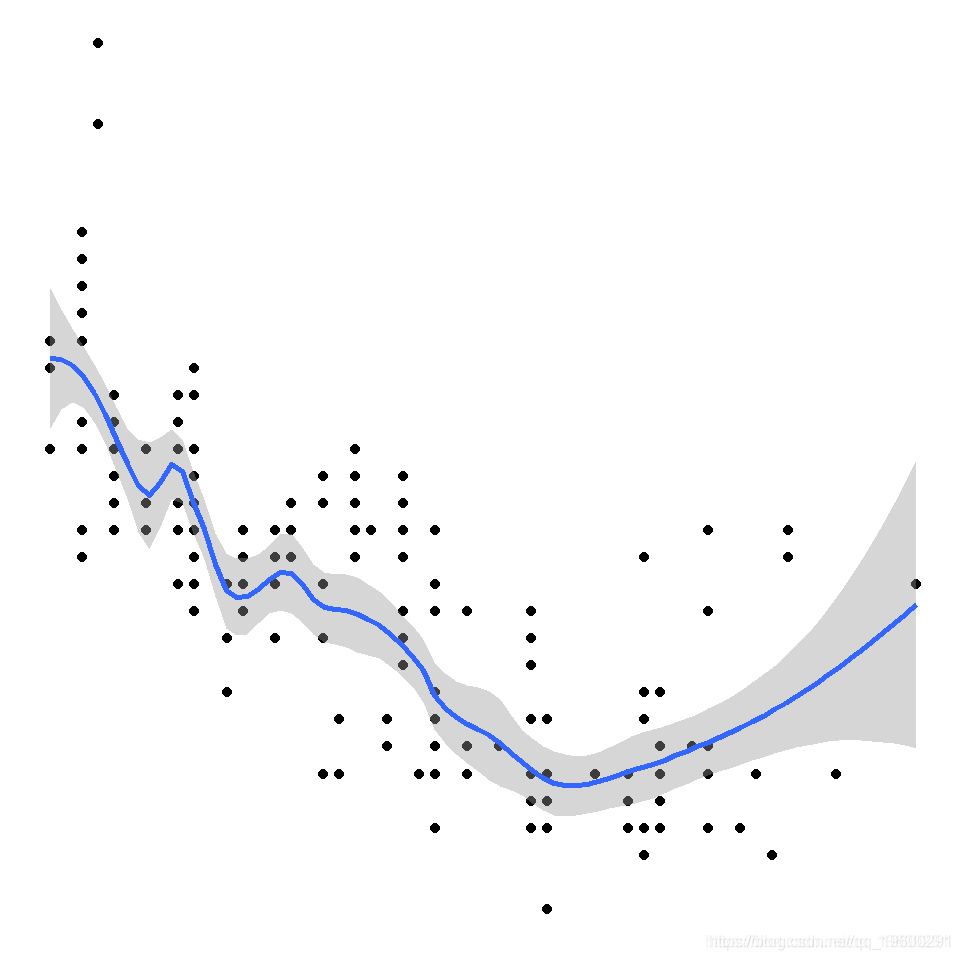
GAM是由数据驱动而非统计分布模型驱动的非参数回归模型，可对部分解释变量进行线性拟合，对其他因子进行光滑函数拟合。模型不需要预先设定参数模型，模型通过解释变量的平滑函数建立，能够自动选择合适的多项式。GAM属于非参数回归模型中的一种，非参数回归不需要模型满足线性的假设前提，可以灵活的探测数据间的复杂关系，但是当模型中的自变量数目较多的时候，模型的估计方差会加大，另外，基于核与光滑样条估计 的非参数回归中自变量与因变量间关系的解释也有难度，1985年Stone 提出加性模型，模型中每一个加性项使用单个光滑函数来估计，在每一加性项中可以解释因变量如何随自变量变化而变化，很好的解决了上述问题。1990年Hastie和Tibshirani扩展了加性模型的应用范围，提出了广义加性模型。
理论
让我们从高斯线性模型的方程开始 ：
GAM中发生的变化是存在光滑项：
这仅意味着对线性预测变量的贡献现在是函数f。从概念上讲，这与使用二次项（
）或三次项（
）作为预测变量没什么不同。
在这里，我们将重点放在样条曲线上。在过去，它可能类似于分段线性函数。
例如，您可以在模型中包含线性项和光滑项的组合
或者我们可以拟合广义分布和随机效应
一个简单的例子
让我们尝试一个简单的例子。首先，让我们创建一个数据框，并创建一些具有明显非线性趋势的模拟数据，并比较一些模型对该数据的拟合程度。
x <- seq(0, pi * 2, 0.1)
sin_x <- sin(x)
y <- sin_x + rnorm(n = length(x), mean = 0, sd = sd(sin_x / 2))
Sample <- data.frame(y,x)library(ggplot2)
ggplot(Sample, aes(x, y)) + geom_point()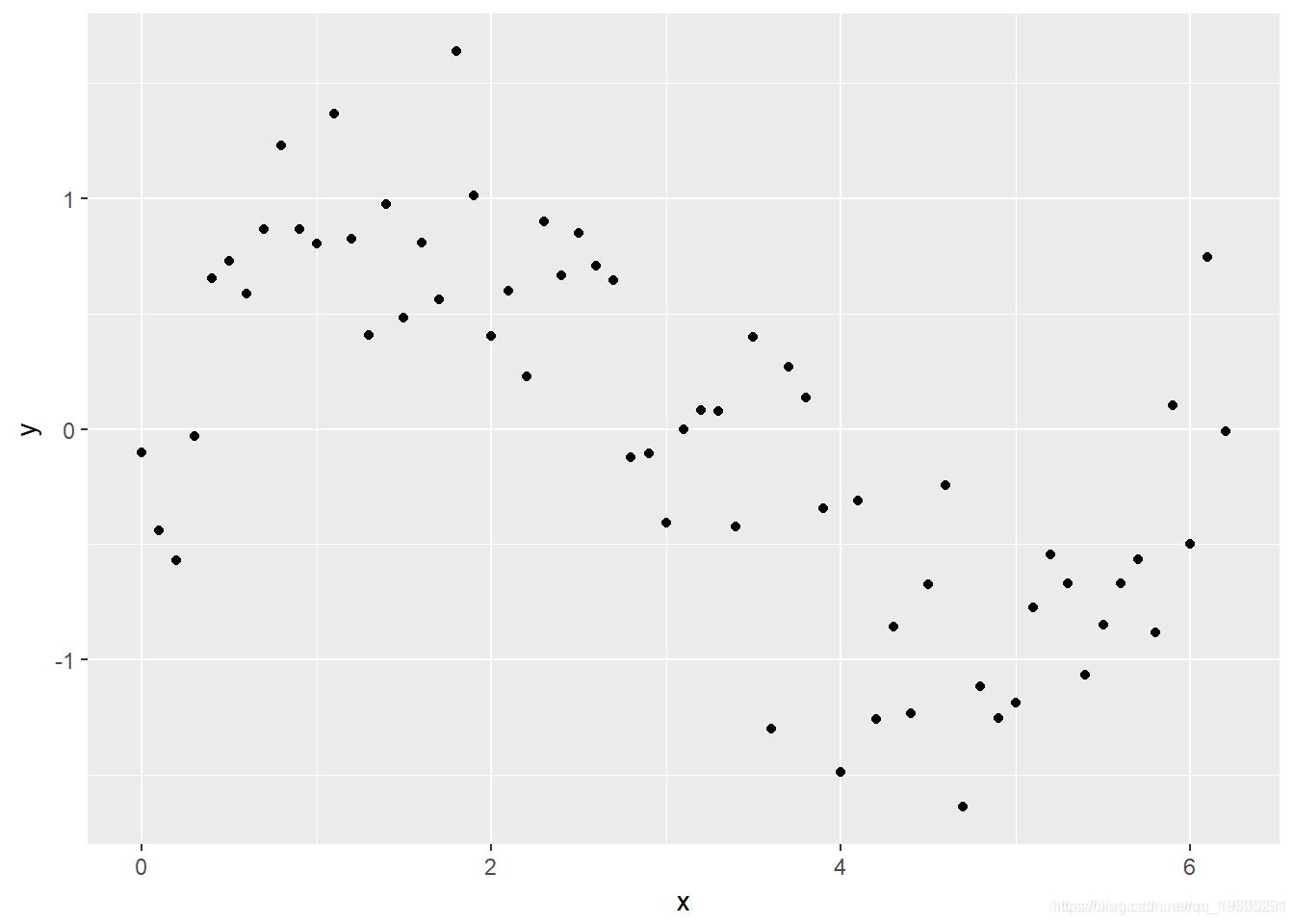
尝试拟合普通的线性模型：
lm_y <- lm(y ~ x, data = Sample)并使用geom_smooth in 绘制带有数据的拟合线 ggplot
ggplot(Sample, aes(x, y)) + geom_point() + geom_smooth(method = lm)随时关注您喜欢的主题
查看图或 summary(lm_y)，您可能会认为模型拟合得很好，但请查看残差图
plot(lm_y, which = 1)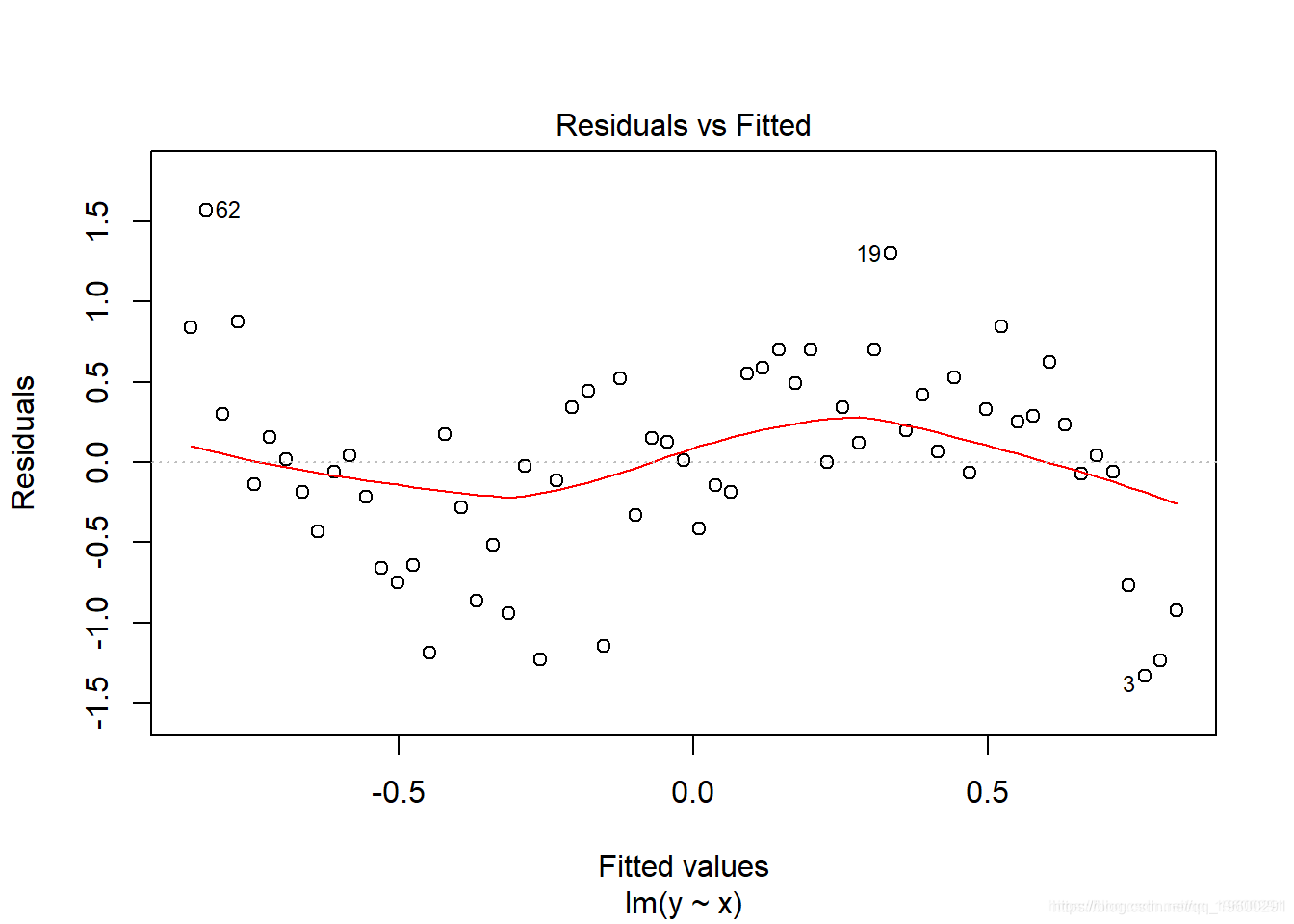
显然，残差未均匀分布在x的值上，因此我们需要考虑一个更好的模型。
运行分析
在R中运行GAM。
要运行GAM，我们使用：
gam_y <- gam(y ~ s(x), method = "REML")要提取拟合值，我们可以predict ：
predict(gam_y, data.frame(x = x_new))但是对于简单的模型，我们还可以利用中的 method = 参数来 geom_smooth指定模型公式。
您可以看到该模型更适合数据，检查诊断信息。
check.gam 快速简便地查看残差图。
gam.check(gam_y)
对模型对象使用summary将为您提供光滑项（以及任何参数项）的意义，以及解释的方差。
##
## Method: REML Optimizer: outer newton
## full convergence after 6 iterations.
## Gradient range [-2.37327e-09,1.17425e-09]
## (score 44.14634 & scale 0.174973).
## Hessian positive definite, eigenvalue range [1.75327,30.69703].
## Model rank = 10 / 10
##
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## s(x) 9.00 5.76 1.19 0.9在这个例子中，非常合适。“edf”是估计的自由度——本质上，数量越大，拟合模型就越摇摆。大约为1的值趋向于接近线性项。
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x)
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.01608 0.05270 -0.305 0.761
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(x) 5.76 6.915 23.38 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.722 Deviance explained = 74.8%
## -REML = 44.146 Scale est. = 0.17497 n = 63光滑函数项
如上所述，我们将重点介绍样条曲线，因为样条曲线是最常实现的光滑函数（非常快速且稳定）。那么，当我们指定s(x)时实际发生了什么 ？
好吧，这就是我们说要把y拟合为x个函数集的线性函数的地方。默认输入为薄板回归样条-您可能会看到的常见样条是三次回归样条。三次回归样条曲线具有 我们在谈论样条曲线时想到的传统 _结点_–在这种情况下，它们均匀分布在协变量范围内。
基函数
我们将从拟合模型开始，记住光滑项是一些函数的和，
首先，我们提取_基本函数_集 （即光滑项的bj（xj）部分）。然后我们可以画出第一和第二基函数。
model_matrix <- predict(gam_y, type = "lpmatrix")
plot(y ~ x) 
matplot(x, model_matrix[,-1], type = "l", lty = 2, add = T)
lines(y_pred ~ x_new, col = "red", lwd = 2)
现在，让我们绘制所有基函数的图，然后再将其添加到GAM（y_pred）的预测中。
现在，最容易想到这样-每条虚线都代表一个函数（bj），据此 gam 估算系数（βj），将它们相加即可得出对应的f（x）的贡献（即先前的等式）。对于此示例而言，它很好且简单，因为我们仅根据光滑项对y进行建模，因此它是相当相关的。顺便说一句，您也可以只使用 plot.gam 绘制光滑项。
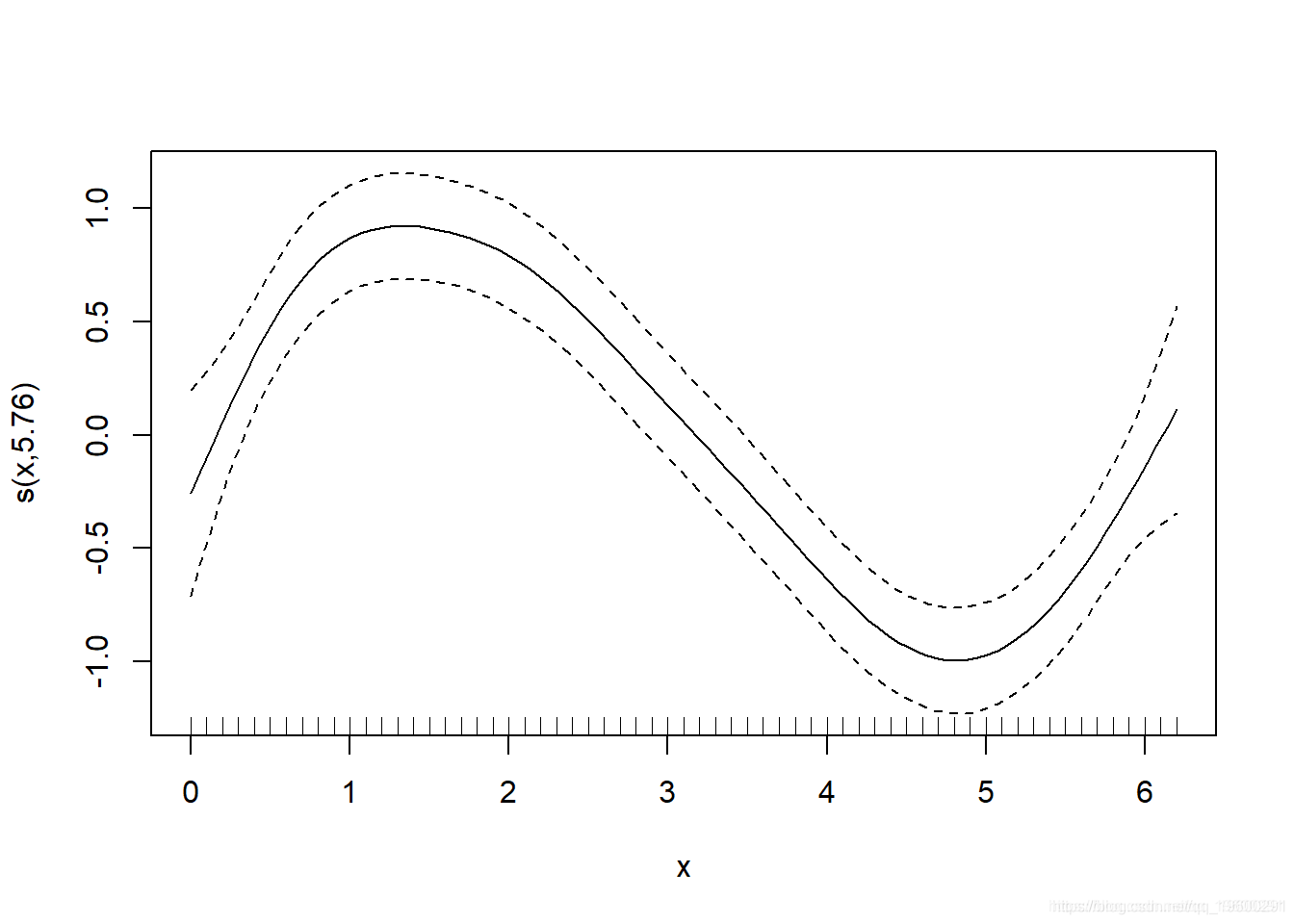
好的，现在让我们更详细地了解基函数的构造方式。您会看到函数的构造与因变量数据是分开的。为了证明这一点，我们将使用 smoothCon。
x_sin_smooth <- smoothCon(s(x), data = data.frame(x), absorb.cons = TRUE)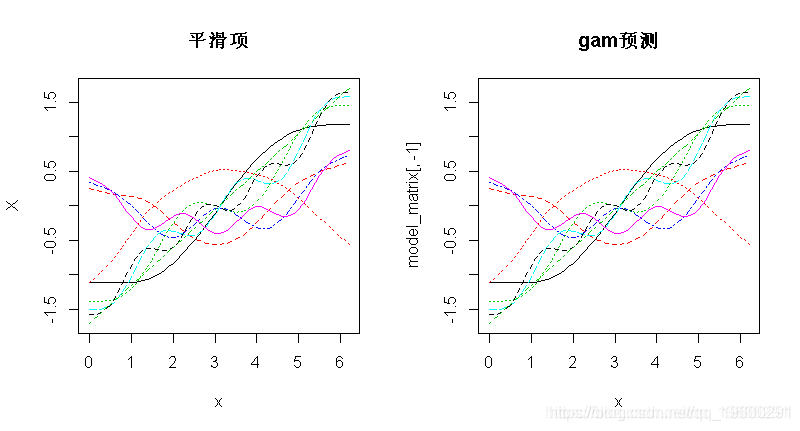 
现在证明您可以从基本函数和估计系数到拟合的光滑项。再次注意，这里简化了，因为模型只是一个光滑项。如果您有更多的项，我们需要将线性预测模型中的所有项相加。
betas <- gam_y$coefficients
linear_pred <- model_matrix %*% betas 
请看下面的图，记住这 X 是基函数的矩阵。
通过 gam.models ， smooth.terms 光滑模型类型的所有选项，基本函数的构造方式（惩罚等），我们可以指定的模型类型（随机效应，线性函数，交互作用）。
真实例子
我们查看一些CO2数据，为数据拟合几个GAM，以尝试区分年度内和年度间趋势。
首先加载数据 。
CO2 <- read.csv("co2.csv")我们想首先查看年趋势，因此让我们将日期转换为连续的时间变量（采用子集进行可视化）。
CO2$time <- as.integer(as.Date(CO2$Date, format = "%d/%m/%Y")) 我们来绘制它，并考虑一个平稳的时间项。
我们为这些数据拟合GAM
它拟合具有单个光滑时间项的模型。我们可以查看以下预测值：
plot(CO2_time)
请注意光滑项如何减少到“普通”线性项的（edf为1）-这是惩罚回归样条曲线的优点。但如果我们检查一下模型，就会发现有些东西是混乱的。
par(mfrow = c(2,2))
gam.check(CO2_time)
残差图的上升和下降模式看起来很奇怪-显然存在某种依赖关系结构（我们可能会猜测，这与年内波动有关）。让我们再试一次，并引入一种称为周期光滑项。
周期性光滑项fintrannual（month）由基函数组成，与我们已经看到的相同，只是样条曲线的端点被约束为相等，这在建模时是有意义的周期性（跨月/跨年）的变量。
现在，我们将看到 bs = 用于选择光滑器类型的k = 参数和用于选择结数的 参数，因为三次回归样条曲线具有固定的结数。我们使用12结，因为有12个月。
s(month, bs = 'cc', k = 12) + s(time)让我们看一下拟合的光滑项：
从这两个光滑项来看，我们可以看到，月度光滑项检测到CO2浓度的月度上升和下降——从相对幅度（即月度波动与长期趋势）来看，我们可以看出消除时间序列成分是多么重要。让我们看看现在的模型诊断是怎样的：
par(mfrow = c(2,2))
gam.check(CO2_season_time)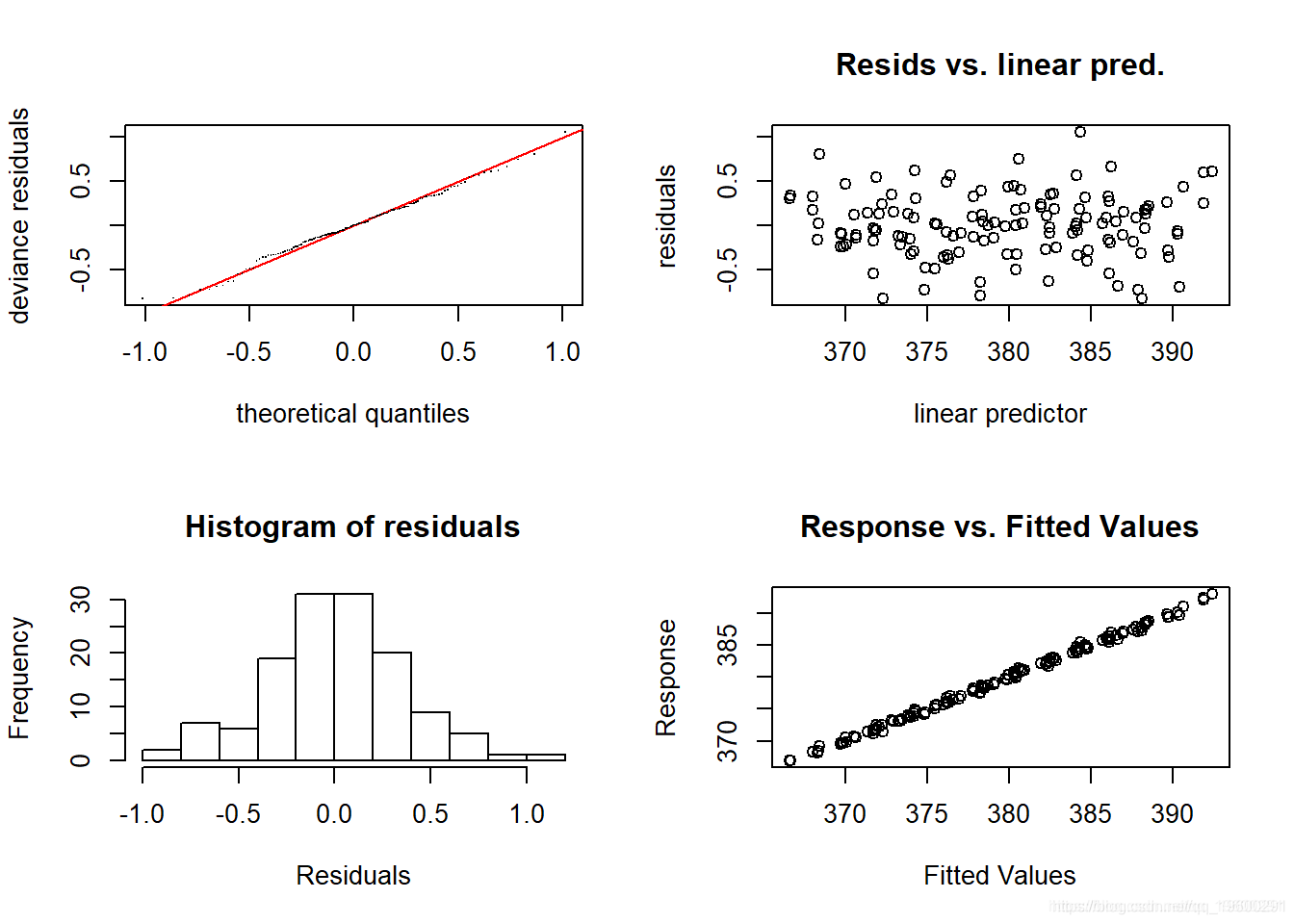
好多了。让我们看一下季节性因素如何与整个长期趋势相对应。
plot(CO2_season_time)
结果
从本质上讲，您可以将GAM的模型结果表示为任何其他线性模型，主要区别在于，对于光滑项，没有单一系数可供推断（即负、正、效应大小等）。因此，您需要依靠视觉上解释光滑项（例如从对plot（gam_model）的调用）或根据预测值进行推断。当然，你可以在模型中包含普通的线性项（无论是连续的还是分类的，甚至在方差分析类型的框架中），并像平常一样从中进行推断。事实上，GAM对于解释一个非线性现象通常是有用的，这个非线性现象并不直接引起人们的兴趣，但在推断其他变量时需要加以解释。
您可以通过plot 在拟合的gam模型上调用函数来绘制局部效果 ，还可以查看参数项，也可以使用 termplot 函数。您可以ggplot 像本教程前面所述那样使用 简单的模型，但是对于更复杂的模型，最好知道如何使用predict预测数据 。
geom_line(aes(y = predicted_values)
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
MATLAB图注意力网络GAT多标签图分类预测可视化
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
