数据读取和处理是金融分析中非常重要的一步。
为了减少误差，在估计时我们可以对每个交易日的收盘价进行自然对数处理，即对日收益率进行计算。
本文通过R软件对金融数据帮助客户进行读取和处理，并进行了收益率波动图、收益率序列的平稳性检验、自相关图和偏自相关图以及ARCH效应检验等分析。通过这些分析，我们可以更好地理解和预测金融市场的变化。
可下载资源
数据读取和处理
为减少误差，估计时根据每个交易日的收盘价对日收益率进行自然对数处理，即收益率r=log(/)。
×
ARCH模型（Autoregressive Conditional Heteroskedasticity Model）全称自回归条件异方差模型”，解决了传统的计量经济学对时间序列变量的第二个假设（方差恒定）所引起的问题。这个模型是获得2003年诺贝尔经济学奖的计量经济学成果之一。之前我们学过的大部分模型都是预测被解释变量的期望值，而ARCH，GARCH模型预测的是被解释变量的方差。ARCH模型能准确地模拟时间序列变量的波动性的变化，它在金融工程学的实证研究中应用广泛，使人们能更加准确地把握风险（波动性）。 该系列模型主要针对汇率、利率、股票价格指数等时间序列所应用，该时间序列的主要特征是：
1、过程的方差不仅随时间变化，而且有时变化得很激烈。
2、按时间观察，表现出“波动集群”特征，即方差在一定时段中比较小，而在另一时段中比较大。
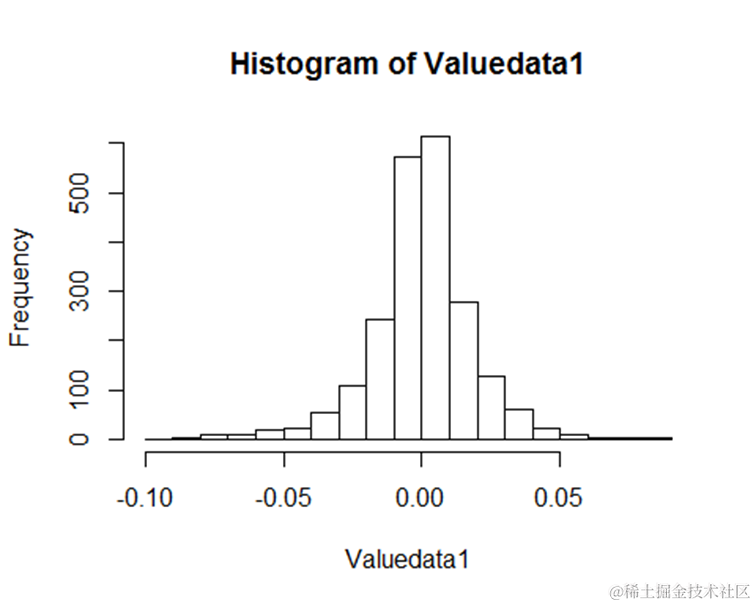
3、从取值的分布看表现为“高峰厚尾”特征，即均值附近与尾区的概率值比正态分布大，而其余区域的概率比正态分布小。
##读取数据
golddata=read.csv("数据.csv")
head(golddata)
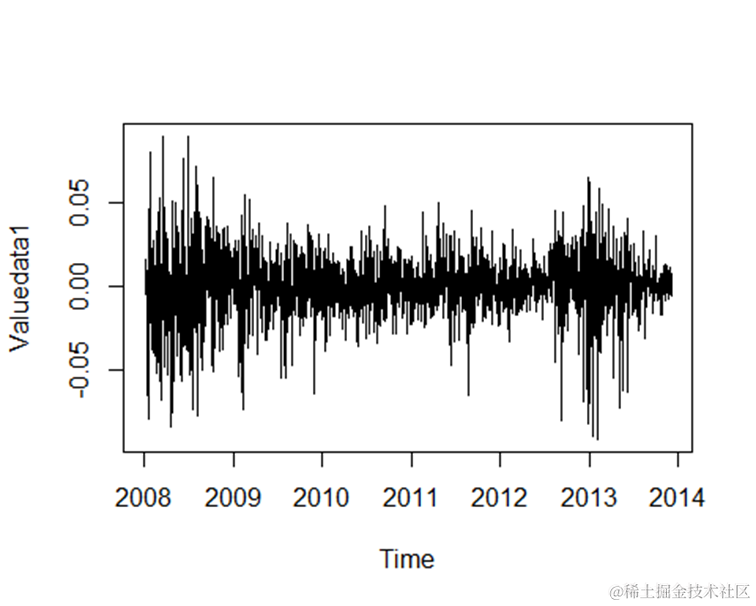
datadesc(Valuedata1)
收益率序列的平稳性检验（ADF检验）
平稳性检验最常用的方法为单位根方法，运用R软件，对日收益率进行单位根检验，检验结果如下
从单位根检验结果可看出： 单位根检验的p-value小于相应临界值0.05，从而拒绝原假设，表明 收益率 不存在单位根，是平稳序列，即服从I(0)过程
通过R软件画出 日收益率的自相关图和收益率的偏自相关图
随时关注您喜欢的主题
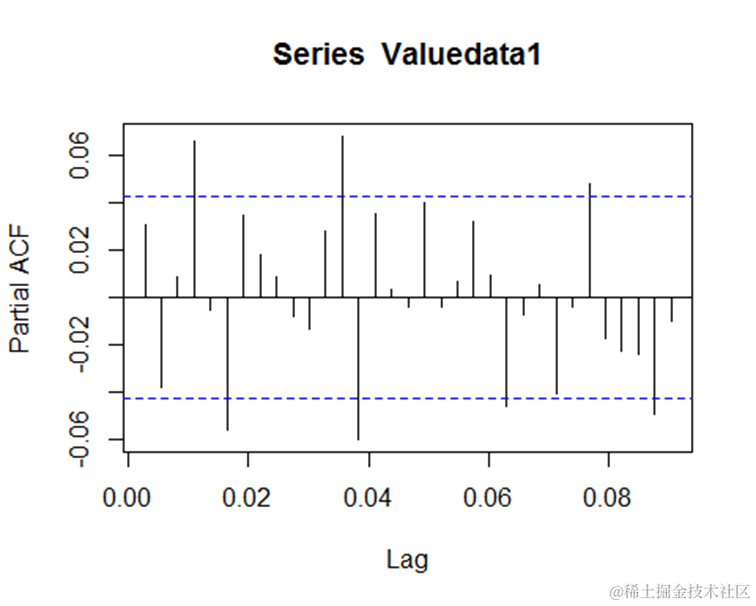
根据Chi-squared最小原则可以看出滞后1期为最优，故选择滞后阶数为1，则公式可以写成。
2.残差序列自相关检验（日收益率的残差和残差平方自相关图）
从序列残差图中可以看出，相关系数基本落入蓝色虚线（95%置信区间）内
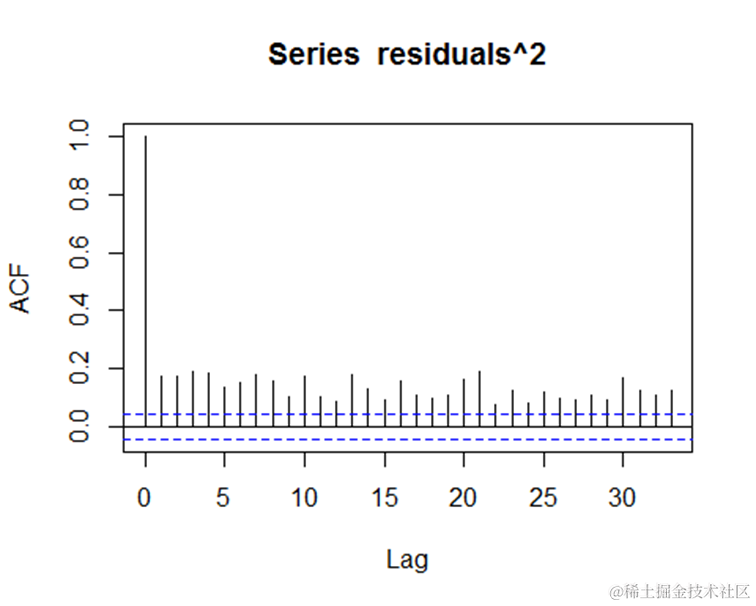
即表明：日收益率残差不存在显著的自相关。而从残差平方图中可看出，相关系数都没落入蓝色虚线（95%置信区间）内，即表明：日收益率的残差平方有显著的自相关，显示出ARCH效应。
3.对残差平方做线性图
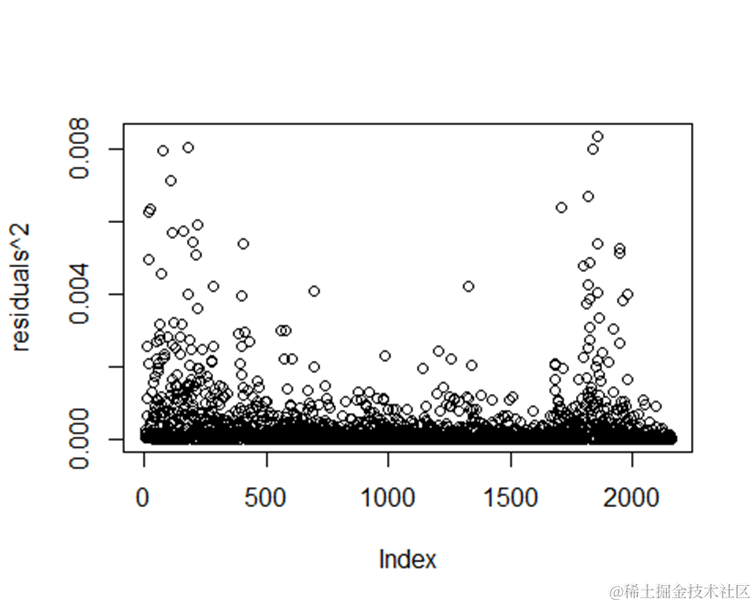
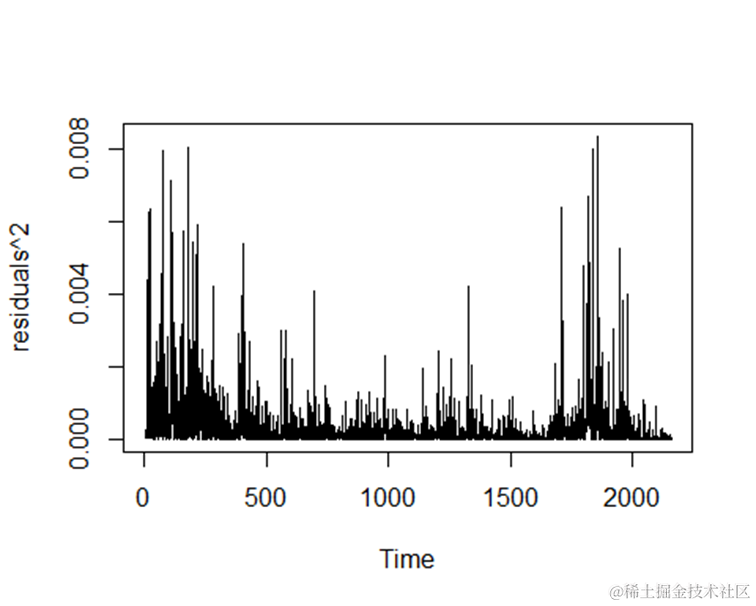
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
马尔可夫转换MSVAR模型预测资产收益率时间序列可视化分析|附数据代码
Python时间序列分析苹果股票数据：分解、平稳性检验、滤波器、滑动窗口平滑、移动平均、可视化
R语言马科维茨Markowitz均值-方差(风险投资模型)分析最优投资组合数据预期收益率可视化
